ОММО 2023
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Точка — середина отрезка
; точка
— середина отрезка
; для каждого
точка
— середина отрезка
.
Пусть
— предельное положение точки
при
. Найдите длину отрезка
, если длина отрезка
равна
Источники:
Подсказка 1
Порисуйте эти точки на отрезке. В каком порядке они будут располагаться?
Подсказка 2
Они будут идти как-то так: S, R_2, R_4..., R,...R_3, R_1, T. Еще осталось понять, чему равна длина отрезка вида R_{n+2}R_n и дело в шляпе!
Обозначим , тогда
- середина отрезка
для каждого
. Легко видеть, что на отрезке точки будут
расположены в следующем порядке:
Поэтому
Далее, длина отрезка в два раза меньше длины отрезка
, откуда длина отрезка
в четыре раза меньше
длины отрезка
. Значит,
Ошибка.
Попробуйте повторить позже
При каком наименьшем можно покрасить каждое натуральное число в один из
цветов так, чтобы любые два числа, отличающиеся на
5 , на 8 , на 10 , на 13 и на 18, были покрашены в разные цвета?
Источники:
Подсказка 1
Давайте попробуем как-то снизу оценить кол-во цветов. Вот что можно заметить в этих разностях: 18-13 = 5, 18-10 = 8, 13-5 = 8, 13-5 = 8....может быть можно найти какую-то группу чисел, в которой все числа должны быть разного цвета?
Подсказка 2
Например, подойдет четверка чисел вида n, n+5, n+10, n+18! А еще подойдет четверка n, n+5, n+13, n+18...теперь проверьте, может ли быть ровно 4 цвета?
Подсказка 3
Для четырех не вышло, давайте попробуем для 5! Может попробовать разбить все числа на какие-то группы, что внутри одной группы разность между числами либо очень маленькая, либо очень большая...тогда, скорее всего, условие выполнится)
Докажем для начала, что четырьмя и меньше цветами обойтись не удастся. Посмотрим на числа . Разности между
ними равны
т.е. любые два из этих чисел покрашены в различные цвета. Значит, цветов хотя бы четыре. Предположим, что цветов ровно четыре.
Тогда числа покрашены во все возможные цвета. Аналогично можно получить, что во все возможные цвета
покрашены числа
,
. Значит, для каждого натурального
числа
и
должны быть покрашены в один
и тот же цвет.
Применим полученное утверждение для . Тогда числа
покрашены в один и тот же цвет. Противоречие,
ведь
и числа 11 и 29 должны быть покрашены в разные цвета.
Докажем теперь, что пять цветов достаточно. Для этого разобьём все натуральные числа на группы по 5 подряд идущих чисел, а группы
покрасим так: первую - в первый, вторую - во второй, ..., пятую - в пятый, шестую - в первый, седьмую - во второй, .... При такой раскраске
числа одного цвета будут или отличаться не более чем на 4, если лежат в одной пятёрке, или хотя бы на 21 - если в разных. Значит, числа,
отличающиеся на и 18, будут покрашены в разные цвета.
Ошибка.
Попробуйте повторить позже
На заводе имеются в достаточном количестве три сплава титана, алюминия и молибдена. Все сплавы с примесями. Процентное содержание компонентов в этих сплавах приведено в таблице.
| 1 | 2 | 3 | |
| Молибден | | | |
| Титан | | | |
| Алюминий | | | |
Из этих сплавов необходимо приготовить новый сплав, в котором алюминия должно быть не больше , а молибдена - не меньше
.
Какое наибольшее и какое наименьшее содержание титана (в процентах) может быть в этом сплаве?
Источники:
Подсказка 1
Давайте сначала просто посчитаем. Пусть мы взяли x,y и 1-x-y первого, второго и третьего сплавов соответственно. Тогда как выглядят наши условия на нужный сплав и что мы хотим максимизировать/минимизировать?
Подсказка 2
Вы получили условия в виде неравенства для x и y, и выражение, которое надо максимизировать/минимизировать. Может быть, на плоскости эти неравенства будут нагляднее?)
Подсказка 3
Нам по факту надо найти макс/мин выражения 6+30x+15y. Понятно, что минимум будет в точке (0, 0). А чтобы найти максимум, можно заметить, что коэф при x больше, чем коэф при y....)
Первое решение.
Заметим, что как бы ни изготавливали новый сплав, содержание титана в нём будет не меньше минимального из содержаний
титана в имеющихся сплавах. Поэтому содержание титана в любом изготовленном сплаве будет не менее . С другой
стороны, сплав 3 подходит под условия на содержание алюминия и молибдена. Значит, наименьшее содержание титана
.
Теперь найдём наибольшее содержание титана в таком сплаве. Заметим, что если при изготовлении нового сплава мы использовали сплав 2, то можно его заменить на сплав 1: от этого содержание алюминия уменьшится, а молибдена и титана - увеличится. Поэтому в сплаве с наибольшим содержанием титана не участвует сплав 2.
Сразу отметим, что тогда в таком сплаве будет молибдена, т.е. он подходит под условие на молибден. В сплаве 1 титана больше, чем
в сплаве 3 , но сплав 1 не подходит под условие на алюминий. Понятно, что чем меньше мы возьмём сплава 3, тем больше будет титана в
изготовленном сплаве. Возьмём ровно столько, чтобы выполнилось условие на алюминий:
и
масса сплава 1 и 3
соответственно), откуда
, т.е. можно взять 23 части сплава 1 и 17 частей сплава 3. Тогда содержание титана в процентах
будет
Второе решение.
Пусть взято и
первого, второго и третьего сплава соответственно, причём
. Тогда условия
задачи можно записать так:
Изобразим на координатной плоскости область (см. рисунок), удовлетворяющую системе неравенств
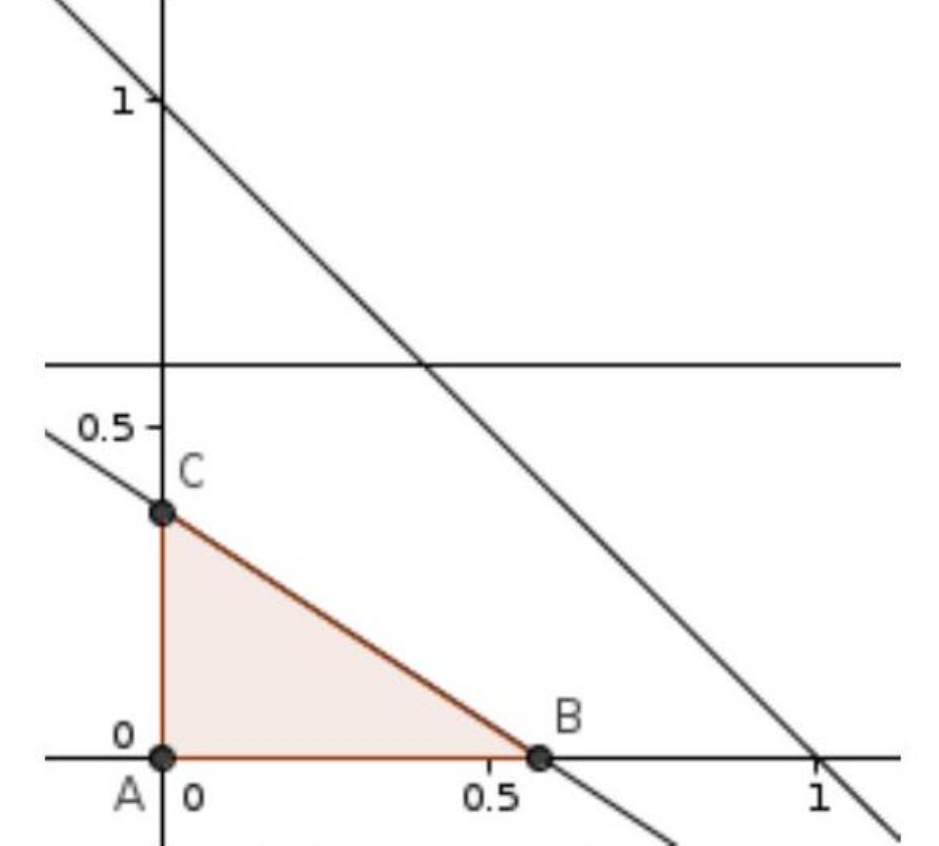
Процентное содержание титана . Легко видеть, что минимум этого числа достигается в точке
и равен 6 . Чтобы найти максимум, заметим, что абсцисса точки
равна
, а ордината точки
. При этом
коэффициент при
в
больше. Значит, значение в точке
точно больше (мы большее число умножаем на большее число), и равно
наименьшее
наибольшее
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и боковыми сторонами
. Точка
на прямой
такова, что
периметр треугольника
наименьший из возможных. Найдите этот периметр.
Источники:
Подсказка 1
Заметим, что основание у нашего треугольника зафиксировано. То есть на самом деле нам нужно найти минимальную сумму расстояний до точки P от A и B. Давайте попробуем понять, почему расстояние будет минимальным, когда лучи PA и PB будут падать под одним углом на BC. Обычно когда речь идёт о минимуме или максимуме, то нужно неравенство, а в геометрии чаще всего — это неравенство треугольника. Как можно попробовать сделать из отрезков PA и PB треугольник, в котором мы явно будем видеть их сумму?
Подсказка 2
Верно, хоть до этого и не просто догадаться, давайте попробуем отразить точку D симметрично относительно BC. Что тогда у нас получается? Пусть симметричная точка X. Получается треугольник APX, где сумма наших расстояний это AP+PX. Но тогда записав неравенство треугольника, когда достигается минимум?
Подсказка 3
Да, получается, чтобы сумма расстояний выстроилась в одну прямую, а это и будет минимум по неравенству треугольника, нужно как раз равенство углов. Победа! Теперь осталась только техническая часть поиска двух сторон равнобедренного треугольника APD. Это можно сделать, например, через теорему Пифагора для половины основания, высоты и стороны треугольника. Нужно только найти высоту трапеции, что при наличии стольких данных несложно.
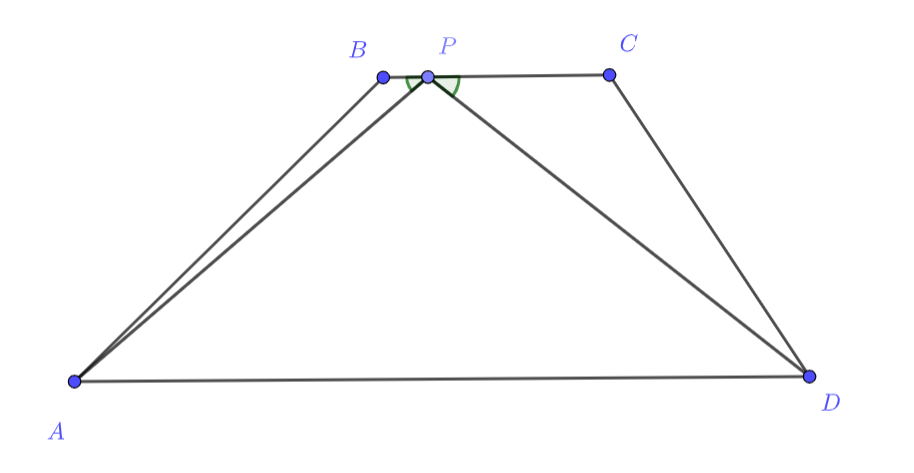
Первое решение.
Воспользуемся следующим утверждением, которое наиболее известно как «принцип наименьшего времени Ферма» в физике:
Для данных точек и данной прямой
из всех точек
сумма
будет минимальной, когда углы между прямыми
и
и
и
будут равны.
Тогда для искомой точки на прямой
должно выполняться равенство
(точки
и
- где-то «далеко» на
прямой
. Поскольку
, то
т.е. треугольник - равнобедренный. Значит, нам достаточно найти периметр равнобедренного треугольника
, где
- точка
на прямой
.
По теореме Пифагора этот периметр равен
где - расстояние между прямыми
и
, т.е. высота трапеции.
Найти высоту трапеции можно разными способами. Например, проведём через точку , прямую, параллельную
, до пересечения с
основанием
в точке
. Тогда искомая высота - это высота из вершины
в треугольнике
. Поскольку
параллелограмм, то
,
.
Итого, нам достаточно найти длину высоты на сторону длины 7 в треугольнике со сторонами 5 , . По формуле площади и
формуле Герона имеем
откуда
и окончательный ответ .
Второе решение.
Также, как и в первом решении, найдём высоту трапеции. Покажем здесь, как можно это было сделать по-другому. Опустим высоты
и
трапеции. Обозначим их длины через
, длину отрезка
обозначим через
. Поскольку
, для
получим
. Из прямоугольных треугольников
и
по теореме Пифагора получим
и
Подставив в эти равенства известные длины, получим систему уравнений
Вычитая из первого равенства второе, получим , откуда
. Тогда
.
Рассмотрим треугольник . Обозначим
, тогда
(здесь и далее все расстояния со знаком, т.е. могут быть
отрицательные). Опустим высоту
. Тогда треугольник
прямоугольный и по теореме Пифагора
Аналогично, из прямоугольного треугольника
Тогда периметр треугольника равен
Найдём производную этой функции:
Из уравнения получаем
откуда . Несложно видеть, что
именно точка минимума, откуда минимальный периметр равен
.
Ошибка.
Попробуйте повторить позже
Решите систему уравнений
Источники:
Подсказка 1
Сразу понимаем, что, скорее всего, эта система "нормально" не решается. У нас два уравнения с кучей неизвестных. Но одно из решений мы сразу угадываем — это один из x равен 3, а остальные 0. Давайте поделим обе части первого уравнения на 3¹⁰. Как тогда можно оценить каждое из слагаемых?
Подсказка 2
Ага, тогда понятно, что каждое из слагаемых не превосходит единицы, так как степень у них чётная. Значит, для любого 1≤k≤92 получаем, что |x_k/3|≤1. Не забываем про модуль, так как извлекаем корень из чётной степени. Но раз у нас число меньше 1 то, что можно сказать о нём при возведении в степень?
Подсказка 3
Верно, тогда это число в 33 степени меньше, чем в 10. Теперь, учитывая это, попробуйте записать неравенство для второго и первого уравнения, используя неравенство с модулем. Выходит, что возможен только случай равенства |x_k/3|³³ = |x_k/3|¹⁰ для данных k.
Заметим, что
Тогда для каждого имеем
откуда
Окончательно получим
Значит, для каждого выполнено
откуда
Отсюда несложно получаем, что тогда один из равен
а все остальные равны
Ошибка.
Попробуйте повторить позже
Укажите все значения параметра , при которых множество решений неравенства
для представимо в виде двух непересекающихся интервалов.
Источники:
Подсказка 1
Давайте сделаем естественную вещь в таком не очень хорошем параметре. У нас есть синус и косинус с одинаковым аргументом. Тогда попробуем сделать замену sin(t)=y и cos(t)=x. Какие условия тогда у нас будут?
Подсказка 2
Верно, тогда у нас получается система из 4 условий: основное тригонометрическое тождество, ограничение на t, ОДЗ знаменателя и само исходное неравенство. Тогда как теперь можно сформулировать вопрос задачи и найти а?
Подсказка 3
Ага, получается, что нам удовлетворяют все решения системы, где точки лежат на полуокружности и ниже, чем график y = |x− a|, который двигается вдоль оси х в зависимости от а. Осталось только определить, когда получается два непересекающихся отрезка в решении и найти из графика граничные точки для а.
Пусть . Тогда, с учётом допустимых значений
, неравенство равносильно системе
Решения этой системы - точки на полуокружности , лежащие ниже графика функции
.

При изменении параметра график функции
перемещается вдоль оси
. При значениях
, близких к
в
качестве множества решений имеем
непересекающихся интервала. При значениях
, близких к
получается
интервала.
Крайнее положение графика, при котором получается два интервала, изображено на рисунке:

Координаты точки пересечения окружности и прямой
равны
Так как , то
.
Таким образом, ответом является множество
Ошибка.
Попробуйте повторить позже
Дано действительное число , отличное от
и
Решите уравнение
Ответ может зависеть от
Источники:
Подсказка 1
Давайте представим, что мы раскрыли скобки и избавились от знаменателей, что мы получим?
Подсказка 2
Мы получим уравнение 6-й степени! А значит, у него точно не больше 6 корней. Тогда есть соблазн попробовать угадать эти 6 корней...
Подсказка 3
Легко видеть, что t - корень. Какие замены можно попробовать сделать, чтобы найти ещё немного корней?
Подсказка 4
Левая дробь не меняется при замене x на 1-x и на 1/x, поэтому получаем новые корни, какие? Попробуйте набрать как можно больше.
Подсказка 5
Теперь лишь остаётся доказать, что при данных ограничениях на t шесть корней, которые вы нашли, всегда различные.
Докажем два утверждения:
- если
- решение уравнения, то и
также решение; действительно,
поэтому если второе равняется , то и первое - тоже.
- если
- решение уравнения, то и
также решение; действительно,
поэтому если второе равняется , то и первое - тоже.
Заметим теперь, что - точно корень исходного уравнения. Тогда, корнями являются также числа
, а тогда и
.
Можно показать, что при данных ограничениях на получившиеся 6 чисел - различны. Кроме того, исходное уравнение при
равносильно уравнению 6 -й степени, которое не может иметь больше 6 корней. Значит, найденные числа и есть все
корни.
Ошибка.
Попробуйте повторить позже
В треугольнике точки
— середины сторон
а
,
— точки касания этих сторон со вписанной
окружностью соответственно. Прямые
пересекают
в точках
и
Докажите, что прямая
делит отрезок
пополам.
Источники:
Подсказка 1
Один отрезок делит другой пополам, часто это происходит потому что они являются диагоналями некоторого параллелограмма.
Подсказка 2
В данном случае окажется, CXC1Y - параллелограмм, но нужно как-то подобраться к точкам X и Y...
Подсказка 3
В этом нам поможет лемма 255, согласно ней точки X и Y лежат на биссектрисах углов A и B соответственно.
Докажем, что точки лежат на биссектрисах углов
соответственно (это утверждение известно как задача
и может быть
использовано на олимпиаде без доказательства). Так как
и
то
следовательно,
и
Аналогично
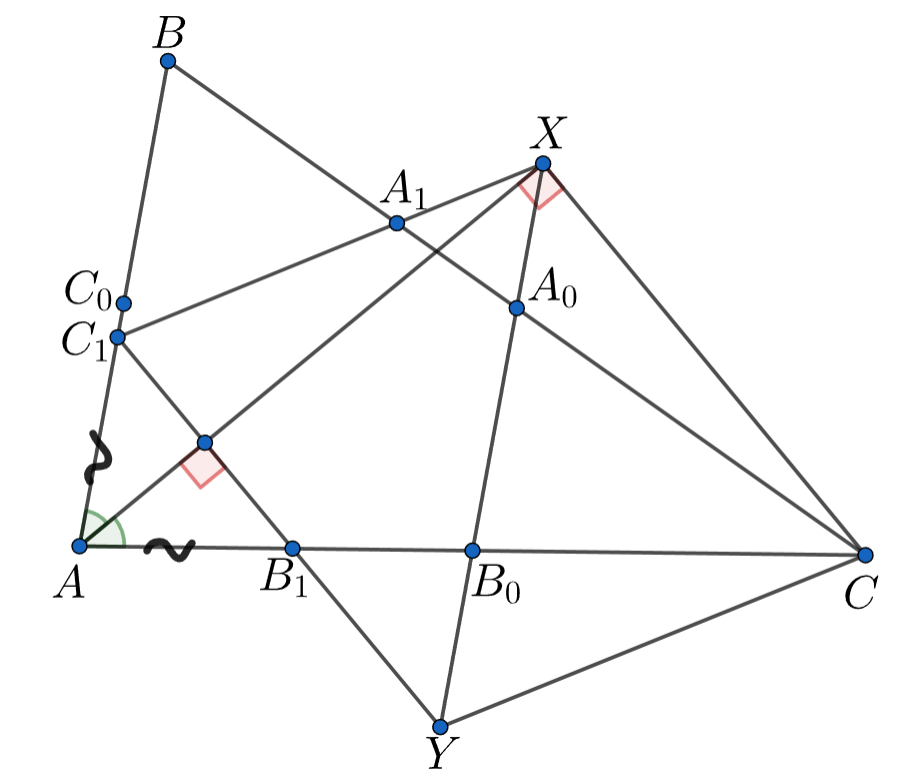
Итак, по лемме
и
потому что треугольник
равнобедренный и
в нём биссектриса,
проведённая к основанию. Следовательно,
Аналогично
Таким образом, четырёхугольник
—
параллелограмм. В таком случае его диагонали точкой пересечения делятся пополам, это даёт нам требуемое.
Ошибка.
Попробуйте повторить позже
Найдите все функции , для которых существует такое вещественное число
, что при всех вещественных
выполнено
равенство
Источники:
Подсказка 1
Заметим, что правая часть несимметрична относительно x и y, а левая - симметрична) Как тогда можно связать x и y?
Подсказка 2
f(x)f(y) - f(x) - 2y + a = 2f(xy+3)=f(y)f(x) - f(y) - 2x + a ⇒ f(x) - 2x = f(y) - 2y. Значит, разность f(x) - 2x постоянна! Как тогда записать f(x) и что с этим можно сделать?
Подсказка 3
f(x) = 2x + C, для некоторого действительного C и любого x) Остается лишь подставить это в равенство из условия, найти C и a)
Заметим, что
Значит, при всех выполнено
. Значит, разность
постоянна и
, для некоторого
. Подставляя в исходное равенство, получаем, что при всех
выполнено равенство:
Оно тождественно выполнено только при ; при этом
Ошибка.
Попробуйте повторить позже
В группе из 80 человек некоторые знакомы друг с другом (знакомства взаимны). Известно, что в группе есть человек, который знает ровно 1 из оставшихся, человек, который знает ровно 2 из оставшихся, ..., человек, который знает ровно 54 из оставшихся. Докажите, что в группе есть три человека, каждые два из которых знакомы.
Источники:
Подсказка 1
Зачастую в задачах на знакомства, на какие-то дороги, где нам даны количества "соединений", удобнее всего начинать с объекта, у которого их больше всех) Попробуем рассмотреть всех знакомых человека А, у которого их 54, что можно о них сказать?
Подсказка 2
Чего же мы хотим добиться от такого множества? Найти человека B в нём, у которого с A точно есть общий знакомый. Но чтобы найти такого B, нужно хотя бы понимать, сколько у него знакомых. Но далеко не обо всех людях мы знаем количество их друзей :( Значит, попробуем сократить множество, в котором будем искать такого B. О скольких людях в множестве друзей A мы точно знаем количество знакомых?
Подсказка 3
В множестве знакомых A максимум 26 человек, у которых мы не знаем количество друзей, значит, есть как минимум 28 человек, про которых мы можем что-то сказать. Какого тогда человека мы можем "выцепить" оттуда, чтобы, наконец, найти B из подсказки 2?
Подсказка 4
Среди них есть человек B, у которого хотя бы 28 знакомых! Осталось лишь доказать, почему же у B и A обязательно есть общий знакомый из всех, при условии, что они знакомы между собой?)
Посмотрим на человека , который знает ровно
из оставшихся. Из них максимум
людей, про количество знакомых у которых в
условии ничего не сказано. Осталось как минимум 28 человек, про количество знакомых которых сказано в условии. Среди них тогда
найдётся человек
, количество знакомых которого хотя бы
У кроме
есть ещё
знакомых, а у
, кроме
ещё
Поскольку
то у
и
есть хотя бы один
общий знакомый
Тройка
и есть искомая тройка человек.


