Тема БИБН - задания по годам

БИБН 2023

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела бибн - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#49716

Дан треугольник, у которого длины сторон — числа рациональные. Докажите, что рациональным числом является

а) отношение $R :r,$ где $R$ и $r$ — радиусы описанной и вписанной окружности;

б) значение $α β γ sin 2 ⋅sin 2 ⋅sin 2,$ где $α,$ $β,$ $γ$ — углы треугольника.

Источники: БИБН-2023, 11.3 (см. www.unn.ru)

Показать доказательство

Первое решение.

Введём длины сторон, как $a,b,c∈ ℚ,$ $S$ — площадь, $a+b+c- p = 2 ∈ ℚ$ — полупериметр. Далее воспользуемся формулами $abc ∘---------------- S =pr = 4R = p(p− a)(p− b)(p− c),$ откуда

R abcp abc r =-4S2-= 4(p-− a)(p-− b)(p−-c) ∈ℚ

Для углов известно $α+ β+ χ= π,$ зная это, распишем произведение

( ) ( ) sin αsin βsin χ-= 1 cos α−-β− cosα-+-β sin π−-α−-β= 1 cosα-− β-− cosα-+β cosα+-β= 2 2 2 2 2 2 2 2 2 2 2

= 1(cosα+ cosβ − cos(α +β)− 1)= 1(cosα+ cosβ +cosχ− 1) 4 4

Осталось воспользоваться теоремой косинусов. Например, для угла $χ$ имеем

2 2 2 c = a + b − 2abcosχ =⇒ cosχ ∈ℚ

То есть косинусы также рациональны, откуда следует рациональность произведения.

Второе решение.

а)

$PIC$

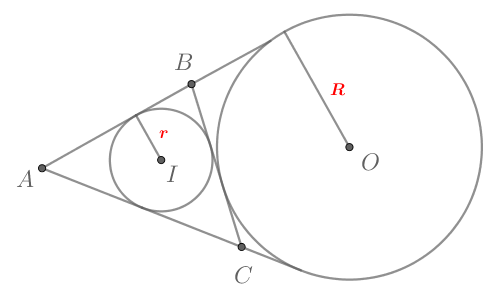
Мы знаем, что $S = pr,$ где $S$ — площадь треугольника, а $p$ — его полупериметр. С другой стороны, $S = abc, 4R$ где $a,$ $b,$ $c$ — стороны треугольника. Тогда

r= S, R = abc p 4S

Следовательно,

abc S- abc⋅p- R :r= 4S :p = 4S2

По формуле Герона

S2 = p(p− a)(p− b)(p− c)

Тогда

abc⋅p abc R:r= 4p(p− a)(p-− b)(p−-c) = 4(p-− a)(p−-b)(p−-c)

Заметим, что здесь каждый из множителей рационален, а следовательно и отношение рационально.

б) Запишем теорему синусов:

AB-- AC-- BC-- sinγ = sinβ = sinα =2R

Отсюда получаем

AB =2R sinγ, AC = 2Rsinβ, BC = 2R sinα

Пусть $I$ — точка пересечения биссектрис треугольника $ABC.$ Рассмотрим треугольник $BIC$ и запишем для него теорему синусов:

BC BI CI sin(90∘+-α)-= sinγ-= sinβ- 2 2 2

$PIC$

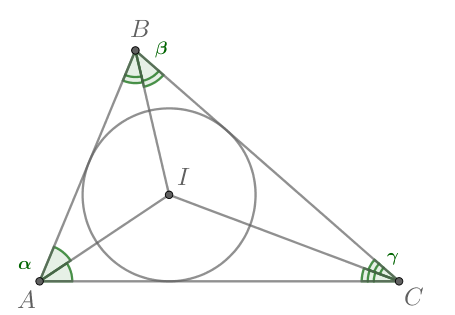
Подставим $BC = 2Rsinα,$ распишем синус двойного угла и синус суммы, получим

4R sinα cosα BI CI ---co2sα--2-= sinγ-= sin-β 2 2 2

Отсюда получаем

$pict$

Аналогично

β γ AI = 4R sin2 sin2

Заметим, что

$pict$

Таким образом,

α β γ r r sin2-⋅sin2 ⋅sin2 = 4R-sinβ-sinγ-⋅4Rsin-αsin-γ⋅ 2 2 2 2 ⋅----r-----= ---------r3--------- 4Rsin α2 sin β2 43R3sin2 α2 ⋅sin2 β2 ⋅sin2 γ2

Тогда

3 α 3 β 3 γ -r3- α- β γ -r- sin 2 ⋅sin 2 ⋅sin 2 = 43R3 ⇒ sin 2 ⋅sin 2 ⋅sin 2 = 4R

По предыдущему пункту $R:r$ рационально, значит и $r:4R$ рационально.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68259

Решите неравенство

2cos(cosx)> 1

Источники: БИБН-2023, 11.1 (см. www.unn.ru)

Показать ответ и решение

Первое решение.

Так как

π π −3 < −1≤ cosx ≤1 <-3,

то неравенство верно для любого $x,$ поскольку тогда

− π3 < cosx < π3 =⇒ cos(cosx)> 12

Второе решение.

Как известно, $cosx∈ [− 1,1],$ откуда $cos(cosx)∈[cos(cos1),1].$ Осталось показать, что

2coscos1> 1 ⇐⇒ coscos1>1∕2⇐ coscos1 >cos1> cosπ∕3= 1 2

То есть неравенство выполнено для всех $x.$

Ответ:

$x ∈ℝ.$

Ошибка.
Попробуйте повторить позже

Задача 3#68260

Решите уравнение

√ ---- √----x √---- √ ----x √---- ( 2023+ 2022)− ( 2023− 2022) = 8088

Источники: БИБН-2023, 11.2 (см. www.unn.ru)

Показать ответ и решение

Заметим, что $√8088-=2√2022,$ отсюда нетрудно видеть, что $x= 1$ является решением. Далее покажем, что функция в левой части строго возрастает на всей числовой прямой. Действительно, мы видим разность возрастающей (основание больше 1) и убывающей (основание меньше 1) показательных функций, которая строго возрастает. Отсюда равенство имеет не более одного решения, которое уже было найдено.

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 4#68261

Дано несколько прямоугольных параллелепипедов в пространстве. Известно, что у каждой пары параллелепипедов есть хотя бы одна общая точка, а их рёбра соответственно параллельны. Обязательно ли все параллелепипеды имеют общую точку?

Источники: БИБН-2023, 11.4 (см. www.unn.ru)

Показать ответ и решение

Поскольку у параллелепипедов ребра соответственно параллельны, мы можем ввести декартову систему координат, направив оси вдоль трех ребер, смежных с одной вершиной (которая станет началом координат) выбранного параллелепипеда. В этой системе координат ребра всех параллелепипедов будут параллельны осям. Спроектировав на ось $Ox$ данный $i$ -ый параллелепипед $(i= 1,2,...,n),$ получим отрезок, который обозначим $[ai,bi].$ Любая пара таких отрезков имеет непустое пересечение (в противном случае соответствующая пара параллелепипедов не пересекается).

_________________________________________________________________________________________________________________________________________________________________________________

Таким образом, приходим к такой задаче: на числовой прямой есть попарно пересекающиеся отрезки $[ai,bi],(i=1,2,...,n),$ и требуется доказать, что у них имеется общая точка.

Опытные олимпиадники могут сразу сослаться на теорему Хелли. Мы же приведём её доказательство, чтобы не оставлять у неопытных читателей чувство неловкости.

_________________________________________________________________________________________________________________________________________________________________________________

Пусть $A$ —- наибольшее значение среди левых концов отрезков, т.е. $A= max{ai|i=1,...n},$ и аналогично, пусть $B$ — наименьшее значение среди правых концов отрезков. Тогда $A ≤B,$ так как в противном случае $ai > bj$ для некоторых $i$ и $j,$ а значит, $i$ -ый и $j$ -ый отрезки не пересекаются. Отсюда следует, что любая точка отрезка $[A,B]$ будет общей для всех наших отрезков. Итак, пусть точка $x∗$ принадлежит проекциям на ось Ох всех параллелепипедов. Точно так же мы можем найти общие точки $y∗$ и $z∗$ проекций на оси $Oy$ и $Oz.$ Тогда точка с координатами $(x∗,y∗,z∗)$ будет принадлежать всем параллелепипедам.

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 5#68262

(a) Докажите, что первые 11 натуральных чисел $1,2,...,11$ нельзя переставить так, чтобы соседние числа отличались либо на 3, либо на 5.

(b) Можно ли сделать это для чисел $1,2,...,12?$

Источники: БИБН-2023, 11.5 (см.www.unn.ru)

Показать ответ и решение

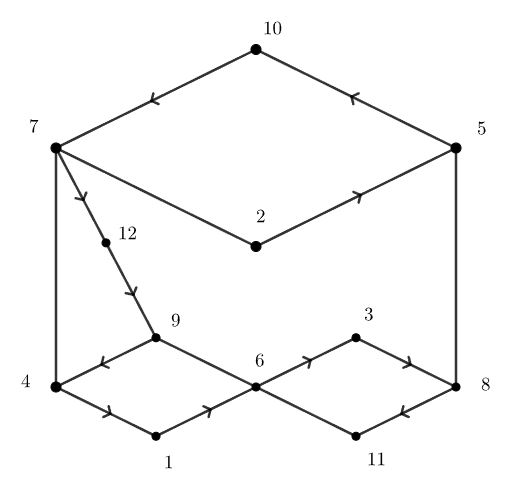
(a) Начертим граф возможных соседей. Рассмотрим три пары вершин в четырехугольниках на графе (они отмечены жирными точками), а именно: (2, 10), (1, 9) и (3, 11) — это вершины с наименьшей степенью (количеством соседей), равной 2.

$PIC$

Предположим, от противного, что есть простой путь на графе (т.е. без повторения вершин), проходящий через все вершины. Тогда найдется такая пара вершин среди трех указанных пар, что путь не начинается и не кончается в вершинах из этой пары (такая пара есть, т.к. концов у пути — два, а пар — три). Таким образом, обе вершины этой пары — “проходны”, но если впервые будет пройдена одна вершина из этой пары, то вторая вершина станет изолированной («отрезанной»: в неё нельзя будет попасть потом). Противоречие.

(b) Пример перестановки: 2, 5, 10, 7, 12, 9, 4, 1, 6, 3, 8, 11. Граф (см. рисунок) помогает построить подобный пример.

Ответ: б) можно