Тема Бельчонок - задания по годам

Бельчонок 2023

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела бельчонок - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#69399

У бельчонка есть 5 орехов, 8 грибов и 11 ягод. Сколькими способами он может выложить все эти предметы в ряд так, чтобы никакие две ягоды не лежали рядом?

Источники: Бельчонок-2023, 11.1 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

На расположение ягод есть ограничение, а вот грибы и орехи мы можем класть как захотим. Полезным будет посмотреть, сколькими способами мы можем выложить в ряд только орехи и грибы без ягод.

Подсказка 2

Ягоды не должны лежать рядом друг с другом. Значит, теперь, когда мы разложили грибы и орехи, у нас есть 14 позиций под ягоды, при этом в каждое место мы можем положить не более одной ягоды. Вычислите, сколькими способами мы можем это сделать. По какому правилу теперь можно посчитать общее количество случаев?

Показать ответ и решение

Первое решение.

Выложим в ряд орехи и грибы — сделать это можно $5 C13$ способами. Далее рассмотрим позиции между выложенными орехами и грибами и по краям от них — получим 14 мест для ягод. Остаётся выложить их туда $11 C14$ способами.

Второе решение.

Сначала объединим орехи и грибы в неягоды, откуда получим 13 неягод и 11 ягод. Далее назовём нейтроном пару (неягода, ягода).

Если на крайней левой позиции в ряду лежит неягода, то 11 ягод образуют нейтроны, поскольку рядом с ними не могут находиться другие ягоды, и левее каждой точно есть неягода. Отсюда имеем 11 нейтронов и 2 дополнительные неягоды. В итоге получаем $2 C13$ способов поставить эту неягоду, то есть 78 расстановок.

Если на крайней левой позиции лежит ягода, то остаются только 10 ягод, каждая из которых попадает в свой нейтрон. Получаем 10 нейтронов и 3 неягоды, откуда имеем $C313 = 286$ расстановок.

Получаем $364= C314$ расстановки. Остаётся вспомнить, что неягоды делятся на два вида. Чтобы учесть это, домножим все способы на $51!3!⋅8!,$ то есть число способов расставить $5$ орехов среди тринадцати неягод, откуда и получаем ответ.

Ответ:

$C5 ⋅C11 13 14$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#69400

Дан прямоугольный треугольник $KLM$ с прямым углом $M.$ На его катете $LM$ длины 52 как на диаметре построена окружность $ω.$ Из точки $K$ к этой окружности проведена касательная $KD,$ отличная от $KM.$ Перпендикуляр $DH,$ опущенный на отрезок $LM,$ пересекает отрезок $KL$ в точке $E.$ Найдите площадь треугольника $LDE,$ если известно, что $LH :MH =4 :9.$

Источники: Бельчонок-2023, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Для начала попробуем найти всё, что можем)) Воспользуемся всеми условиями на LH, LM, MH и найдем их) Тогда будет несложно найти оставшиеся отрезки на LM и DH! На картинке много прямых углов...что хочется сделать?

Подсказка 2

Найти среди них подобные! Учтём, что угол между касательной и радиусом прямой, тогда какие треугольники будут подобными (или даже равными)?

Подсказка 3

Треугольники MKO и KOD будут равными, тогда треугольники LHD и OKM будут подобны! Найдём отношение KM/LM. Теперь нам необходимо найти площадь треугольника LED, как можно это сделать?

Подсказка 4

Найдя его высоту и стороны! Высота его это LH, а в каких подобных треугольниках этот отрезок встречается, чтобы его найти?

Подсказка 5

Треугольники LHE и LMK подобны, поэтому несложно найти EH! Осталось лишь найти DE через DH и EH, что сделать из подобия несложно)

Показать ответ и решение

$PIC$

Пусть $O$ — центр окружности $ω.$ Заметим, что

∘ --------- LH =-4LM =16, MH = 36, OH = 1LM − LH = 10, DH = OD2 − OH2 = 24 13 2

Прямоугольные треугольники $LHD$ и $OMK$ подобны, поскольку

∠MLD = 1∠MOD = 1(180∘ − ∠MKD )= 90∘ − ∠MKO = ∠MOK 2 2

Тогда

KM-- 1 KM-- 1 DH- 3 LM = 2 ⋅OM = 2 ⋅LH = 4

Из подобия треугольников $LHE$ и $LMK$ мы получаем

3 EH = 4LH = 12

Поэтому

1 1 1 SLDE = 2 ⋅DE ⋅LH = 2 ⋅(DH − EH )⋅LH = 2 ⋅12⋅16 =96

Ответ: 96

Ошибка.
Попробуйте повторить позже

Задача 3#69401

Для положительных чисел $x,y,z$ докажите неравенство

---z2--- ---x2--- ---y2--- ---xy---- --yz---- ---zx--- x +y+ 2z + 2x+ y+ z + x+ 2y+z ≥ x+ y+2z + 2x +y+ z + x +2y+ z

Источники: Бельчонок-2023, 11.3 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Давайте перенесем всё из правой части неравенства в левую и сложим всё, что имеет одинаковые знаменатели. Получаем в левой части неравенства сумму трех очень похожих дробей, а в правой - ноль. Когда имеется такая конструкция, то часто бывает полезным подумать, как можно оценить каждую дробь по отдельности. К тому же, зачастую, если понять, как оценить одну дробь, то мы сразу будем знать, как оценить и остальные.

Подсказка 2

Рассмотрим дробь (z² - xy) / (x + y + 2z). Когда мы говорим про оценки в неравенствах, то в первую очередь в голову приходят неравенства о средних. В этой дроби мы можем много что оценить, знаменатель или числитель целиком, но давайте воспользуемся неравенством средних для xy, чтобы в числителе получить разность квадратов.

Подсказка 3

Раскрыв в числителе разность квадратов, мы можем сократить равные скобки в числителе и в знаменателе и получить оценку на дробь. Аналогично поступим для каждой дроби. Что теперь мы можем сказать про сумму трех дробей?

Показать доказательство

Неравенство из условия равносильно

-z2-− xy- -x2−-yz- -y2−-xz- x+y +2z +2x+ y+ z + x+ 2y+ z ≥ 0

По неравенству о средних $xy ≤(x+2y)2,$ отсюда после применения формулы разности квадратов имеем

2 -z-−-xy--≥ (2z−-x−-y)(2z+-x+-y)-= 2z-− x-− y x+ y+ 2z 4(2z+ x+ y) 4

Аналогично оцениваем два других слагаемых и получаем, что

-z2−-xy-+ -x2−-yz-+ -y2− xz-≥ x+ y+ 2z 2x+ y+ z x+ 2y +z

2z− x− y 2y− z− x 2x− y− z ≥ ----4---+ ---4----+ ---4----= 0

мы доказали треубемое.

Ошибка.
Попробуйте повторить позже

Задача 4#69402

16 команд провели турнир по хоккею, каждая команда сыграла с каждой по разу. За победу начислялось 2 очка, за ничью — 1 очко, за проигрыш очков не давалось. При этом каждые три команды в играх между собой набрали разное количество очков. Какое наибольшее число ничьих могло быть в этом турнире?

Источники: Бельчонок-2023, 11.4 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Пупупу… давайте попробуем получить оценку сверху на количество ничьих! Для этого, попробуйте построить примеры для N=2, 3, 4 и 5. Причём примеры такие, в которых количество ничьих максимально!

Подсказка 2

Да, мы получили оценку на N²/4. Остаётся придумать как доказать, что эта формула работает для любого N!

Подсказка 3

Да, это утверждение мы будем доказывать по индукции! Для этого достаточно рассмотреть две команды, которые сыграли в ничью и подумать, как могли сыграть все другие команды с этими двумя!

Подсказка 4

Так, но мы только показали, что существует такая оценка сверху! Теперь нужно придумать пример такой, что в оценке сверху достигается равенство(пример должен быть для любого N)

Подсказка 5

Для построения примера, попробуйте посмотреть на маленькие N и воспользоваться идеей разбиения элементов от 1 до N на два непересекающихся множества. Также, возможно, Вам придётся строить пример в зависимости от четности N.

Показать ответ и решение

Решим задача для произвольного $N.$ Докажем утверждение, известное в олимпиадных кругах как теорема Турана.

Оценка: Докажем по индукции, что число ничьих не превосходит $N2 4 .$

База индукции: При $N = 2$ это очевидно. При $N = 3$ все три игры не могли закончиться вничью, иначе у всех команд было бы одинаковое число очков.

Шаг индукции: Рассмотрим две команды $A$ и $B,$ сыгравшие вничью. С каждой из остальных команд хотя бы одна из них сыграла не вничью, иначе образуется запрещенная тройка команд. Значит, общее число ничьих в играх с участием этих двух команд не больше $N − 1.$ По предположению индукции в играх между остальными командами было не более $(N−2)2 4$ ничьих. Следовательно, общее число ничьих не превосходит $(N−2)2 2 --4-- +N − 1= N4-.$

Пример: Пронумеруем команды числами от $1$ до $N.$ Пусть каждые две команды с номерами разной чётности сыграли вничью, а в играх между командами с номерами одной чётности победила команда в меньшим номером. Если $N = 2k− 1,$ то $k$ команд имеют нечётный номер и $k− 1$ команда - чётный, поэтому количество ничьих равно $k(k− 1).$ При $N =2k$ получаем по $k$ команд с номерами каждой чётности и $k2$ ничьих. В обоих случаях полученное число равно $[ 2] N4 .$ При этом каждые три команды в играх между собой набрали либо 0, 2 или 4 очка, если имеют номера одной чётности, либо $1,2,3$ очка, если две из них имеют номера одной чётности, а третья - другой.

Замечание. Заметим, что идея примера приходит из двудольного графа, где разная чётность номеров отвечает разным компонентам.

Подставим $N = 16$ и получим ответ.

Ответ: 64

Ошибка.
Попробуйте повторить позже

Задача 5#69403

Решите уравнение

2a a k ℓ 3 + 3 +2 =2 7

в целых неотрицательных числах.

Источники: Бельчонок-2023, 11.5 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Левая часть должна делиться на 7, а еще видно связь между 3^2a и 3^a, что тогда хочется сделать?

Подсказка 2

Хочется заменить 3^a на t и записать табличку остатков на t^2 + t + 2 по модулю 7^l. Тогда какие выводы мы сможем сделать относительно l?

Подсказка 3

l < 2! Остаётся разобрать 2 случая с l) Начнем с l = 0. У нас появляется уравнение относительно a и k, где одно из решений на "маленьких числах" угадывается. Далее попробуем оценить a и доказать, что при a >= 2 решений нет. Как это сделать?

Подсказка 4

При a >= 2 мы можем оценить k и найти остаток от деления на 3 числа 2^k. Теперь мы знаем, какое k, поэтому можем подставить это в изначальное уравнение. Какое уравнение у нас получается и какой вид будет иметь k?

Подсказка 5

k = 2m + 1, тогда мы приходим к уравнению вида 3^a(3^a + 1) = 2(4^m - 1), значит m делится на 3. Теперь мы можем оценить, на что делится 4^m - 1, тем самым сделав выводы о делителях 3^a + 1. Какие?

Подсказка 5

3^a + 1 делится на 7. Осталось лишь оценить a и прийти к противоречию с помощью сравнений по модулю) осталось лишь рассмотреть случай l = 1, что делается теми же идеями, что и случай l = 0)

Показать ответ и решение

Если $ℓ ≥2,$ то получим сравнение

2 ( 2) t +t+ 2≡ 0 mod 7

где $t= 3a.$ Но это сравнение невозможно ни при каком $t$ (проверку осуществляем с перебора остатков по модулю $7).$ Значит, $ℓ∈ {0;1}.$

1.: В случае $ℓ= 0$ имеем уравнение $32a+ 3a+ 2= 2k.$ Если $a =0,$ то $k =2.$ При $a= 1$ решений нет. Далее считаем $a≥2.$ Имеем $k≥ 2$ и $2k ≡ 2(mod 3),$ откуда $k =2m +1$ для некоторого натурального $m.$ Из равенства $3a (3a+ 1)=2 (4m − 1)$ следует, что $m$ делится на 3 (иначе правая часть не будет делиться на 9). Тогда $4m− 1$ делится на $43− 1=7 ⋅9.$ Следовательно, $3a+ 1$ делится на 7. Но тогда $a≡ 3(mod 6),$ так что $3a+ 1≡ 0$ $(mod 33+1).$ Однако $33+ 1≡ 0(mod 4),$ что дает противоречие.
2.: Рассмотрим случай $ℓ= 1.$ При $a= 1$ из уравнения $2a a k 3 +3 + 2= 7⋅2$ находим $k= 1.$ Пусть далее $a ≥2$ и, как следствие, $k≥2.$ Имеем $(a−1 ) a (k−1 ) 3 3 − 1 (3 +4)= 142 − 1 .$ Отсюда следует, что $( a−1 ) a 3 − 1 (3 +4)$ делится на 7. Это возможно только при условии $a ≡1(mod 6).$ Но тогда $a−1 3 − 1≡ 0(mod 8),$ что приводит к противоречию.

Ответ:

$(a,k,ℓ)∈{(0;2;0),(1;1;1)}$

Ошибка.
Попробуйте повторить позже

Задача 6#69404

Андрей, Боря, Вася, Гриша, Денис и Женя после олимпиады собрались в кинотеатр. Они купили билеты на 6 мест подряд в одном ряду. Андрей и Боря хотят сидеть рядом, а Вася и Гриша не хотят. Сколькими способами они могут сесть на свои места с учётом их пожеланий?

Источники: Бельчонок-2023, 11.1 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Реализовать условие, когда Андрей и Боря сидят рядом, несложно (посчитаем количество способов рассадки двоих, а затем рассадим остальным). Осталось лишь реализовать условие на то, что Вася и Гриша не сидят рядом... считать варианты, когда они действительно сидят не рядом, с учётом первого условия сложно. Как тогда сделать лучше?

Подсказка 2

Посчитать варианты, когда в обеих парах мальчики сидят рядом! Осталось лишь понять, как прийти к тому, что нас просят в задаче)

Показать ответ и решение

Число способов рассадки, когда Андрей и Боря сидят рядом, равно $2 ⋅5!= 240$ (достаточно объединить их в одного человека двумя способами). Способов рассадки, при которых и Андрей-Боря, и Вася-Гриша окажутся рядом, равно $2 ⋅2 ⋅4!= 96.$ Поэтому они могут сесть $240− 96 =144$ способами.

Ответ: 144

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#69405

В треугольник $ABC$ вписана окружность $ω$ радиуса $r,$ которая касается стороны $AB$ в точке $P.$ На окружности отмечена точка $R,$ диаметрально противоположная точке $P.$ Прямая $CR$ пересекает сторону $AB$ в точке $Q,$ причём $CA + AQ =1.$ Найдите площадь треугольника $ABC.$

Источники: Бельчонок-2023, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Для начала хочется понять: что вообще делать с условием CA + AQ = 1? Перекинуть равенство на один отрезок - так себе идея. Давайте найдём это же равенство в треугольнике еще раз! Например, попробуем доказать, что CB + BQ = 1) Что можно сделать?

Подсказка 2

Если бы треугольники CBQ и CAQ состояли из касательных к окружности, то было бы удобнее разбираться с этим условием...А может быть, есть треугольники, некоторые стороны которых - касательные к вписанной окружности, и они связаны с CBQ и CAQ?

Подсказка 3

Проведите касательную в точке R к вписанной окружности. С помощью точек пересечения к сторонам треугольника получатся два треугольника. И вот они на самом деле подобны каким-то двум другим треугольникам и обладают очень интересным свойством) Останется применить всё, что знаем, и вспомнить формулу S = pr!

Показать ответ и решение

Проведём через точку $R$ касательную к $ω,$ пересекающую отрезки $AC$ и $BC$ в точках $M$ и $N$ соответственно. Пусть $K$ и $L$ — точки, в которых $ω$ касается сторон $AC$ и $BC$ соответственно.

$PIC$

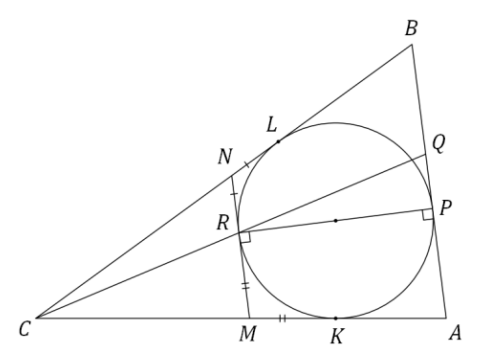
Заметим, что $CM + MR = CM + MK =CK = CL = CN +LN = CN + NR.$ Прямые $AB$ и $MN$ параллельны как перпендикуляры к одному диаметру. Поэтому треугольники $CNR$ и $CBQ,$ а также $CMR$ и $CAQ$ подобны с коэффициентом $k= CCQR.$ Тогда

CB + BQ = k(CN + NR )=k(CM + MR )= CA+ AQ = 1,

откуда

SABC = 1(CA +AB + BC)⋅r= 1(CA +AQ + BQ +CB )⋅r= r 2 2

Ответ:

$r$

Ошибка.
Попробуйте повторить позже

Задача 8#69406

Известно, что $a,b,c> 0$ и $a+ b+c= 1.$ Докажите, что

-----a----- -----b----- -----c----- 3 3a2+ b2+ 2ca + 3b2+ c2+ 2ab +3c2+ a2+2bc ≤ 2

Источники: Бельчонок-2023, 11.3 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Если мы бегло посмотрим на условие, то сразу поймем, что приводить к общему знаменателю здесь это очень плохой вариант. В таких случаях бывает полезно оценить каждое слагаемое по отдельности. К тому же мы видим, что они достаточно похожи, возможно, придумав, как оценить одну дробь, мы сразу поймем, как оценить остальные.

Подсказка 2

Давайте внимательно посмотрим на первую дробь. Понятно, что с числителем тут ничего не сделаешь. А вот в знаменателе у нас есть тут целых два квадрата, стоит попытаться выделить полный квадрат. Подумайте, как нам может в этом помочь условие, что a+b+c=1.

Подсказка 3

Давайте в выражении 3a²+b²+2ac представим 3a² как a² + 2a², тогда можно будет вынести общий множитель из 2ac и 2a². Что можно подставить вместо a+c и как при этом будет выглядеть оценка на 3a²+b²+2ac?

Подсказка 4

Если вместо (a+c) подставить (1-b), то после выделения полного квадрата станет понятно, что 3a²+b²+2ac >= 2a. Используя это знание, оцените всю дробь целиком, остальные дроби суммы и саму сумму.

Показать доказательство

Так как $a+ c= 1− b,$ то $3a2+ b2 +2ca= a2+b2+ 2a(1− b)=2a+ (a− b)2 ≥ 2a.$ Следовательно,

----a------ 1 3a2+ b2+ 2ca ≤2

Аналогично

b 1 c 1 3b2+-c2+2ab ≤ 2; 3c2-+a2+-2bc-≤ 2

Сложив три полученных неравенства, получим

-----a-----+ -----b-----+-----c-----≤ 1+ 1 + 1= 3 3a2+ b2+ 2ca 3b2 +c2+ 2ab 3c2+ a2+2bc 2 2 2 2

Ошибка.
Попробуйте повторить позже

Задача 9#69407

Несколько команд провели турнир по футболу, каждая команда сыграла с каждой по разу. За победу начислялось 3 очка, за ничью — 1 очко, за проигрыш очков не давалось. Команда “Бельчата” заняла первое место, набрав больше всего очков, а команда “Метеор” — последнее место, набрав меньше всего очков. Если бы за победу давали не 3 очка, а 2, то наоборот, команда “Метеор” стала бы первой, а команда “Бельчата” — последней. Найдите наименьшее количество команд, которое могло участвовать в таком турнире.

Подсказки к задаче

Подсказка 1

Давайте попробуем изучить разницу набранных очков указанных команд до и после изменения системы. Подумайте, насколько много побед нужно одержать команде, чтобы она смогла попасть на первое место?

Подсказка 2

Разница между количеством очков команд на первом и на последнем месте хотя бы 2. А могло ли быть такое, что "Метеор" совсем никого не обыграл?

Подсказка 3

"Метеор" обязательно кого-то обыграет, так как иначе у него будет набрано не более половины всех очков. Можно ли провести аналогичные рассуждения про "Бельчат"?

Подсказка 4

Чтобы уменьшение баллов за победу дало "Бельчатам" попасть на последнее место, у них поражений должно быть больше, чем побед! Тогда давайте проследим, как сильно могли измениться баллы "Метеора"? Сколько и каких игр нужно "Бельчонку", чтобы в любом случае упасть ниже соперников?

Подсказка 5

После пересчёта "Метеор" потеряет хотя бы одно очко, тогда несложно посчитать, сколько же очков должны потерять "Бельчата", чтобы условие выполнилось! Не забудьте построить пример ;)

Показать ответ и решение

Оценка: До пересчёта у команды «Бельчата» было хотя бы на 2 очка больше, чем у команды «Метеор», а после пересчёта - хотя бы на 2 очка меньше. Кроме того, чтобы после пересчёта оказаться первой, команда «Метеор» должна иметь хотя бы одну победу. Действительно, в каждом матче разыгрывается 2 очка, поэтому если бы у команды «Метеор» не было побед, то она набрала бы не более половины возможного числа очков и не могла бы стать первой. Аналогично, для того чтобы команда «Бельчата» стала последней, у неё должно быть поражений больше, чем побед. Таким образом, после пересчёта команда «Метеор» потеряет как минимум 1 очко. Следовательно, команда «Бельчата» должна потерять не менее 5 очков, т. е. у неё должно быть не меньше пяти побед и не меньше шести поражений. Поэтому она сыграла как минимум 11 матчей, значит, в турнире участвовало не менее 12 команд.

Пример: Приведён в таблице (первой буквой В обозначен выигрыш, два последних столбца — количество очков до и после пересчета соответственно).


Команда	$Б$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$M$	Сумма 1	Сумма 2

$Б$		B	B	B	B	B	0	0	0	0	0	0	15	10

$2$	0		1	1	1	1	$B$	$B$	$B$	0	0	1	14	11

$3$	0	1		1	1	1	0	$B$	$B$	$B$	0	1	14	11

$4$	0	1	1		1	1	0	0	$B$	$B$	$B$	1	14	11

$5$	0	1	1	1		1	$B$	0	0	$B$	$B$	1	14	11

$6$	0	1	1	1	1		$B$	$B$	0	0	$B$	1	14	11

$7$	$B$	0	$B$	$B$	0	0		1	1	1	1	1	14	11

$8$	$B$	0	0	$B$	$B$	0	1		1	1	1	1	14	11

$9$	$B$	0	0	0	$B$	$B$	1	1		1	1	1	14	11

$10$	$B$	$B$	0	0	0	$B$	1	1	1		1	1	14	11

$11$	$B$	$B$	$B$	0	0	0	1	1	1	1		1	14	11

$M$	$B$	1	1	1	1	1	1	1	1	1	1		13	12

Ответ:

$12$

Ошибка.
Попробуйте повторить позже

Задача 10#69408

Решите уравнение

4 2 2 x + y = xy + y

в натуральных числах.

Источники: Бельчонок-2023, 11.5 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Мы видим, что в уравнении все коэффициенты равны 1. Это наводит нас на мысль о том, что надо искать связь между x и y. У нас есть удобное слагаемое y, поэтому разумно оставить его и попытаться пораскладывать остальные слагаемые...

Подсказка 2

Мы видим, что можно вынести y² за скобку. Тогда получится, что x⁴-y²(x-1)=y. Если отнять от обеих частей 1, можно получить, что (x-1)(x³+x²+x+1-y²)=y-1. Пускай x≠1, тогда y-1 делится на x-1, т.e. y=k(x-1)+1. Теперь можно подставить вместо y k(x-1)+1 и посмотреть, что получится...

Подсказка 3

После подстановки и сокращения на (x-1) можно заметить, что наше равенство имеет вид k-3=(x-1)(...). Тогда k=m(x-1)+3 или m=(k-3)/(x-1). Вспоминаем, что k=(y-1)/(x-1) и получаем, что m=(y-3x+2)/(x-1)². Кажется, что от делимости мы уже ничего не получим. Может тогда попробовать метод оценки...

Подсказка 4

Попробуйте понять, бывает ли целое число m больше или равно 1...

Подсказка 5

Пускай m≥1.Тогда y≥x²+x-1 ⇒ x⁴=(x-1)y²+y≥x⁵+x⁴-3x³+4x-2, что неверно при x>1. Получается, что m<1 ⇔ m≤0. Тогда k может принимать значения 1, 2 или 3. Проверьте эти значения и не забудьте рассмотреть случай x=1!

Показать ответ и решение

Уравнение равносильно