Тема Изумруд - задания по годам

Изумруд 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела изумруд - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79614Максимум баллов за задание: 7

Можно ли в клетках квадрата $6 ×6$ расставить числа от $1$ до $36$ (каждое по одному разу) так, чтобы $6$ сумм по горизонтали и $6$ сумм по вертикали в некотором порядке являлись $12$ последовательными числами?

Источники: Изумруд-2024, 11 (см. izumrud.urfu.ru)

Подсказки к задаче

Подсказка 1

Обозначим первую из 12 последовательных сумм за n. Какие числа входят в эти суммы? Что можно сказать о сумме всех сумм по горизонтали? А по вертикали?

Подсказка 2

Заметим, что при подсчёте всех горизонтальных сумм мы каждое число в таблице посчитали один раз. Тогда чему будет равна сумма всех таких 12ти сумм?

Подсказка 3

Удвоенной сумме всех чисел в таблице. Может ли быть такое? Проверим уравнением

Показать ответ и решение

Предположим, что можно. Сумма всех чисел равна $1+ 2+ 3+ ...+36.$ А удвоенная их сумма равна $n+ (n+1)+ ...+ (n +11).$ Посчитав суммы арифметических прогрессий, получаем

2n+ 11 36 ⋅37 --2---⋅12 = -2---⋅2

2n =211

Противоречие, так как $n ∈ℕ.$

Ответ:

нет

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#79615Максимум баллов за задание: 7

Положительные числа $a,b,c$ таковы, что

2 2 2 a + b +c + 2abc= 1

Докажите, что

a∘ (1− b2)(1-− c2)+b∘ (1−-c2)(1−-a2)+c∘(1−-a2)(1−-b2)≥ 2√abc

Источники: Изумруд-2024, 11 (см. izumrud.urfu.ru)

Подсказки к задаче

Подсказка 1

Рассмотрим подкоренные выражения. Что можно сказать о них? Как использовать условие?

Подсказка 2

Раскрыв скобки под корнями и применив условие, получаем возможность избавиться от корней! Переходим к новому неравенству - очень уж оно напоминает условие;)

Подсказка 3

Получаем, что a^2 + b^2 + c^2 + 3 abc >= 2*sqrt(abc). Как применить условие? Остаётся несложно неравенство, которое очень напоминает кое-что известное!

Показать доказательство

Рассмотрим одно из подкоренных выражений

( 2)( 2) 2 2 22 1− b 1− c = 1− b − c + bc

По условию $1− b2− c2 = a2+2abc$ , поэтому подкоренное выражение равно $(a+ bc)2$ , и, так как $a,b,c> 0$ , $∘ (a+-bc)2 = a+bc$ .

Для оставшихся слагаемых рассуждения аналогичные

√ --- a(a +bc)+b(b+ac)+c(c+ab)≥ 2 abc

2 2 2 √--- a + b + c+ 3abc≥ 2 abc

Пользуясь равенством из условия, получаем

1+abc≥ 2√abc

--- (1 − √ abc)2 ≥0

Верное для любых $a,b,c$ неравенство.

Ошибка.
Попробуйте повторить позже

Задача 3#79616Максимум баллов за задание: 7

Натуральные числа от 1 до 8 расставили по кругу так, что каждое число делится на разность своих соседей. Известно, что числа 2 и 5 стоят рядом. Докажите, что числа 4 и 6 стоят рядом.

Источники: Изумруд-2024, 11 (см. izumrud.urfu.ru)

Подсказки к задаче

Подсказка 1

Будем отталкиваться от того, что нам уже дано. Какие числа можно поставить рядом с 2? Какие - рядом с 5?

Подсказка 2

Рядом с 2 может стоять одно из чисел 3, 4 ,6, 7. Рядом с пятеркой - 1, 3, 7. Переберем случаи! От какого еще числа удобно отталкиваться?

Подсказка 3

Помним, что соседями единицы могут быть только последовательные числа.

Показать доказательство

Рядом с $2$ может стоять одно из чисел $3,4,6,7$ . Рядом с пятеркой — $1,3,7$ . Заметим также, что соседями единицы могут быть только два последовательных числа. Переберем всевозможные варианты для соседа двойки:

1) Рядом с 2 стоит 3. Тогда рядом с 3 может стоять только 1. Ее сосед — это только 4 и рядом с 4 может встать только 6.

2) Рядом с 2 стоит 4. Тогда рядом с 4 может стоять $1,3$ или $6$ .

Ошибка.
Попробуйте повторить позже

Задача 4#79617Максимум баллов за задание: 7

Фигура оборотень бьёт все клетки, находящиеся от неё через клетку слева, справа, сверху или снизу, а также бьёт клетку, на которой стоит. Какое наименьшее количество оборотней необходимо поставить на клетчатую доску $8× 8$ , чтобы эти фигуры били все клетки доски?

Источники: Изумруд-2024, 11 (см. izumrud.urfu.ru)

Подсказки к задаче

Подсказка 1

Оборотни на каких множествах клеток точно друг друга не бьют? Попробуем найти такие участки (множества клеток), на которых мы сможем оценить количество оборотней.

Подсказка 2

Оборотни, стоящие на квадрате 2*2, друг друга точно не бьют. Как, исходя из этого соображения, найти 4 множества клеток, которые замещают всю доску и в которых мы сможем оценить количество оборотней?

Подсказка 3

Рассмотрите множества клеток, получаемые всевозможными путями оборотня из каждой клетки углового квадрата 2*2. В каждом таком множестве по 16 клеток. Осталось лишь оценить количество оборотней в каждом таком множестве!

Показать ответ и решение

Раскрасим клетки доски в $4$ цвета следующим образом: все клетки, куда может прийти оборотень из, не умаляя общности, левой нижней угловой клетки, покрасим в первый цвет. Сдвигами этого множества клеток вправо, вверх и вправо вверх получаем $4$ множества клеток.

$PIC$

Рассмотрим одно из них. Чтобы все клетки были побиты, нужно как минимум $4$ оборотня, так как каждый из них бьет не более $5$ клеток, и, следовательно, $3$ и меньше оборотней бьют максимум $15$ клеток. Пример расстановки $4$ оборотней: выделим $4$ непересекающихся Т-образных фигур, в каждой из которых отметим по одному оборотню.

И так как оборотень, стоящий на клетке из одного множества, не может дойти до клеток из трех других, получаем, что всего нужно как минимум $16$ оборотней.

Ответ: 16

Ошибка.
Попробуйте повторить позже

Задача 5#79618Максимум баллов за задание: 7

Вписанная окружность треугольника $ABC$ с центром в точке $I$ касается сторон $BC,AC, AB$ соответственно в точках $D,E,F$ . Точки $M$ и $N$ симметричны вершине $A$ относительно прямых $DE$ и $DF$ соответственно. Окружности, построенные на отрезках $IE$ и $IF$ как на диаметрах, вторично пересекаются в точке $K$ . Докажите, что $K$ лежит на прямой $MN$ .

Источники: Изумруд-2024, 11 (см. izumrud.urfu.ru)

Подсказки к задаче

Подсказка 1

Хочется с самого начала понять, что за точка K нам дана. Заметим, что одна сторона у наших треугольников одинаковая на будущее. К тому же из условия вытекает, что какие-то углы прямые. Тогда чем же является точка K на нашей картинке?

Подсказка 2

Верно, точка K лежит на отрезке FE и является серединой, так как FIE равнобедренный. Теперь когда объекты на картинке так или иначе связаны, то можно вернуться к вопросу задачи. Что если посмотреть на четырёхугольник NFME. Чем в нём является K? Если же K будет лежать на NM, то что должно выполняться?

Подсказка 3

Верно, K середина диагонали и, если NFME будет параллелограммом, то K как раз будет лежать на NM. Осталось доказать это. Причём мы знаем, что NF =AF = AE = EM, как отрезки касательных из одной точки и симметрии. Остаётся только ввести стандартно углы треугольника, посчитать немного, и победа!

Показать доказательство

Докажем, что точка $K$ является серединой отрезка $F E$ . Действительно, окружности построены на $FI$ и $IE$ как на диаметрах, поэтому

∘ ∠F KI = ∠EKI = 90.

Следовательно, постольку $FI = IE$ и $KI$ — высота равнобедренного треугольника $FIE,$ точка $K$ является серединой его основания.

$PIC$

Теперь достаточно проверить, что четырехугольник $NF ME$ является параллелограммом. Это так, поскольку

NF = AF =AE = EM,

где первое и третье равенство следует из симметрии, а второе верно, поскольку $AF$ и $AE$ являются отрезками касательных, проведенных из одной точки.

Осталось показать, что $NF ||EM.$ Для этого достаточно доказать, что $EM ||BC,$ тогда аналогично $NF ||BC,$ откуда следует требуемое. Последнее верно, ведь

∠(DC,DE )= ∠(DE, EC)= ∠(DE,AE )= ∠(EM, ED ).

где $∠ (DC,DE )$ обозначает угол между $DC$ и $DE$ (с другими аналогично).

Ошибка.
Попробуйте повторить позже

Задача 6#137260Максимум баллов за задание: 7

Вписанная окружность треугольника $ABC$ касается сторон $BC, AC,AB$ соответственно в точках $D,E,F.$ Точки $M$ и $N$ симметричны вершине $A$ относительно прямых $DE$ и $DF$ соответственно. Докажите, что $MENF$ — параллелограмм.

Источники: Изумруд - 2024, 10.3 (см. izumrud.urfu.ru)

Показать доказательство

Треугольник $△CDE$ равнобедренный, из свойств касательных к окружности, значит, прямая $DE$ перпендикулярна биссектрисе угла $C,$ так как биссектриса является высотой, следовательно, прямая $DE$ параллельна внешней биссектрисе угла $C,$ так как биссектрисы смежных углов перпендикулярны, поэтому при симметрии относительно этой прямой, прямая $AC$ перейдёт в прямую параллельную $BC.$ Следовательно $ME$ параллельно $BC,$ аналогично $NF$ параллельно $BC,$ поэтому $ME$ параллельно $NF.$

$PIC$

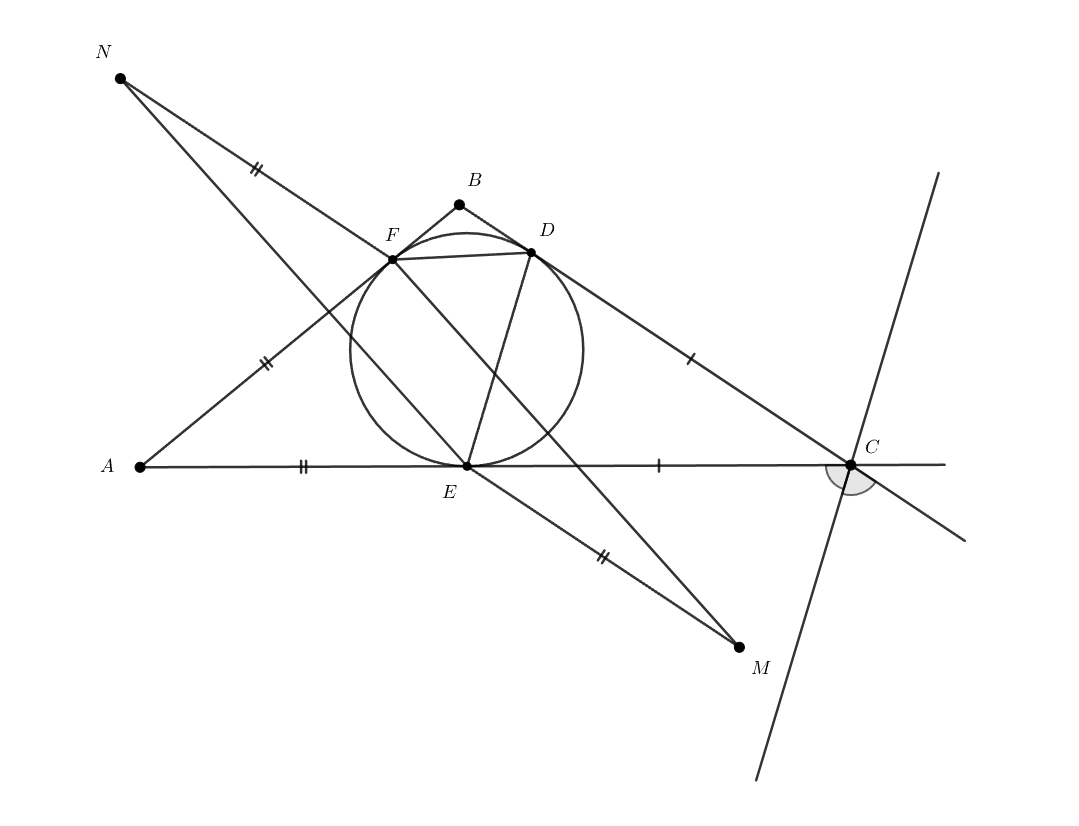
Докажем, что $ME = NF,$ тогда $MENF$ обязан быть параллелограмм. И вправду из симметрии $ME = AE$ и $NF = AF.$ А из свойств отрезков касательных $AE = AF,$ откуда $ME = NF.$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#137263Максимум баллов за задание: 7

Фигура вампир бьёт все клетки, находящиеся от неё через клетку по диагонали слева-сверху, справа-сверху, слева-снизу или справа-снизу, а также бьёт клетку, на которой стоит (см. рисунок). Какое наименьшее количество вампиров необходимо поставить на клетчатую доску $8× 8,$ чтобы эти фигуры били все клетки доски?

$PIC$

Источники: Изумруд - 2024, 10.4 (см. izumrud.urfu.ru)

Подсказки к задаче

Подсказка 1

Самое время вспомнить о раскрасках! Пробуйте разные варианты.

Подсказка 2

Нам было бы удобно, если фиксированный вампир бил в один и тот же цвет. Как битые клетки расположены относительно друг друга?

Подсказка 3

Заметим, что если поделить поле на квадратики 2 на 2, то битые клетки для конкретного вампира будут в одном и том же месте квадратика!

Подсказка 4

Может, стоит как-то раскрасить эти квадратики?

Подсказка 5

Покрасьте клетки квадратиков в 4 цвета так, чтобы в каждой полосе доски цвета чередовались. Чем нам будет это полезно?

Подсказка 6

Клеток каждого цвета одинаковое количество, один вампир бьет за раз 5 клеток, тогда мы построили оценку на количество вампиров. Осталось привести пример!

Показать ответ и решение

Раскрасим шахматную доску в $4$ цвета следующим образом: разобьём доску на квадратики $2$ на $2,$ и все левые верхние углы красим в цвет $1,$ правые верхние в цвет $2,$ и так далее. Тогда вампир бьёт только клетки цвета, на котором он стоит.

Заметим, что клеток цвета $1$ ровно $16,$ а каждый вампир бьёт ровно $5$ клеток. Если на цвете $1$ стоит не больше $3$ вампиров, то суммарно они побьют не больше $15$ клеток. Доказали, что на каждом цвете хотя бы $4$ вампира, а, значит, всего вампиров хотя бы $16.$

Расставим $4$ вампира, которые будут бить все клетки цвета $1.$ Первого вампира поставим в единственную центральную клетку цвета $1.$ Ещё одного на две клетки ниже первого, третьего на две клетки правее, а последнего поставим, так чтобы вампиры образовывали квадрат. Они и вправду бьют все клетки цвета $1,$ забудем, что вампир бьёт клетку, на которой стоит, тогда в этой расстановке, каждый вампир бьёт четыре уникальные клетки, значит, суммарно они бьют $16$ различных клеток. Для других цветов расстановка аналогична.

Ответ: 16

Ошибка.
Попробуйте повторить позже

Задача 8#137264Максимум баллов за задание: 7

Антону очень нравятся нечётные цифры, поэтому все числа, состоящие из нечётного количества цифр, и не содержащие в своей записи чётных цифр, он называет приятными. Остальные числа Антон приятными не считает. Докажите, что существует бесконечно много пар приятных чисел $a$ и $b,$ состоящих из одинакового количества цифр, произведение которых является приятным числом.

Источники: Изумруд - 2024, 10.5 (см. izumrud.urfu.ru)

Показать доказательство

Докажем, что пары чисел $a =N = 4⋅102k−1 3$ и $b= N +2$ подойдут при любом $k.$ Заметим, что

2 M =N (N + 2)=(N +1) − 1

Изучим десятичную запись числа $N,$ для этого заметим

2k 4⋅10 − 1= 399...9

Поэтому $N = 133...3,$ а так как $2k$ четное, то количество троек чётно, поэтому $N$ приятное. Так же видно, что $N + 2$ приятное.

Докажем, что $M$ приятное. Преобразование дают

(4⋅102k-− 1 )2 (4-⋅102k+-2)2 (2⋅102k-+1)2 M = 3 +1 − 1= 3 − 1= 4 3 − 1

Теперь посмотрим на десятичную запись числа

( 2k )2 4k 2k T = 2⋅10-+-1 = 4-⋅10-+-4⋅10--+-1 3 9

После деление числителя на знаменатель в столбик, видно, что $T = 4...48...89,$ при этом в числителе было число с нечётным числом цифр, после деления на $9$ количество цифр уменьшилось на один, значит, в $T$ чётное число цифр. Теперь видно, что

M = 4T − 1= 17...795...56− 1 =17...795...55

При этом число цифр в $M$ на один больше, чем в $T,$ стало быть, это число приятное.