Тема НадЭн - задания по годам

НадЭн 2023

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела надэн - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#71014

Каждый из шести домов, стоящих на одной стороне улицы, соединен кабельными воздушными линиями с каждым из восьми домов на противоположной стороне. Сколько попарных пересечений образуют тени этих кабелей на поверхности улицы, если никакие три из них не пересекаются в одной точке? Считайте, что свет, порождающий эти тени, падает вертикально вниз.

Источники: Надежда энергетики-2023, 11.1 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Нас просят найти количество попарных пересечений! Для начала давайте разберемся, а когда образуется одно попарное пересечение?

Подсказка 2

Да, пересечение образуется, когда мы выбираем два дома на одной стороне(различных), два дома на другой стороне(тоже различных) и делаем биекцию между ними(то есть, соединяем один дом ровно с одним другим). Остаётся посчитать количество таких четверок домов!

Подсказка 3

Первые два дома нужно выбрать из 6, а вторые два из 8. То есть, это просто число сочетаний из 6 по 2 и число сочетаний из 8 по 2!

Показать ответ и решение

Возьмем произвольную пару домов на одной стороне улицы и произвольную пару на другой. Они являются вершинами выпуклого четырехугольника (поскольку две стороны четырехугольника, идущие от каждой выбранной пары, лежат по одну сторону прямой, т.е. углы не превосходят $∘ 180$ ), следовательно, его диагонали пересекаются.

Каждое попарное пересечение теней (кабелей) является точкой пересечения диагоналей такого четырехугольника. Таким образом, осталось найти их количество, которое равно произведению способов выбрать пару домов на каждой стороне улицы.

C26 ⋅C28 = 420.

Ответ: 420

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#71015

Найдите максимальное значение величины $x2+ y2 +z2,$ если известно, что

2 2 2 x +y + z = 3x+8y+ z.

Источники: Надежда энергетики-2023, 11.2 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

На что намекает сумма квадратов?)

Подсказка 2

На квадрат длины вектора! Введем декартову систему координат. С левой части мы разобрались - это квадрат длины вектора (x, y, z). А чем является правая часть?)

Подсказка 3

Правая часть - это скалярное произведение векторов a = (x, y, z) и c = (3, 8, 1). Теперь правую часть можно оценить сверху с помощью длин сомножителей, осталось лишь сделать вывод) Помним, что вектор c - фиксированный!

Показать ответ и решение

Введем декартову систему координат и рассмотрим произвольный вектор $a$ с координатами $(x,y,z)$ и фиксированный вектор $c$ с координатами $(3,8,1)$ . Тогда левая часть условия представляет собой квадрат длины вектора $a,$ а правая — скалярное произведение векторов $a$ и $c :$

2 |a|= (a,c)

Оценивая скалярное произведение через длины сомножителей, получаем

2 |a| ≤|a|⋅|c|⇔ |a|≤ |c|

Как известно, равенство возможно, а достигается при векторах, лежащих на одной прямой. Поэтому максимальное значение будет достигаться, например, при $a = c.$

Подставляя значения, получаем $32+ 82 +11 = 74.$

Ответ: 74

Ошибка.
Попробуйте повторить позже

Задача 3#71016

В уравнении

2022 2021 2020 x − 2x − 3x − ...− 2022x− 2023 =0

можно как угодно переставлять коэффициенты при всех степенях $x$ , кроме самой старшей. Можно ли такой перестановкой добиться, чтобы уравнение имело хотя бы два положительных корня?

Источники: Надежда энергетики-2023, 11.3 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Давайте подумаем, какой в этой задаче может быть ответ: если ответ да, то необходимо предъявить пример. Не очень хочется подбирать коэффициенты и искать корни. Давайте попробуем доказать, что, как бы мы не меняли коэффициенты местами, положительных корней будет не больше 1. На что вас наводит последнее предложение?

Подсказка 2

На монотонность! Вспомните, если функция строго монотонна, то она имеет не более 1 корня. Давайте попробуем найти здесь что-то похожее. Пускай (a₂, a₃, ..., a₂₀₂₃)- произвольная перестановка чисел (2, 3, ..., 2023). Тогда наш многочлен имеет вид: x²⁰²²-a₂x²⁰²¹-...-a₂₀₂₃=0. Нам мешаются минусы, может, перенести их в правую часть?

Подсказка 3

x²⁰²²=a₂x²⁰²¹+...+a₂₀₂₃. Теперь справа у нас монотонная функция, при x>0. Но слева у нас также монотонная функция, поэтому сразу завершить решение не получится. Что можно сделать, чтобы слева у нас стояла константа?

Подсказка 4

Можно поделить обе части на x²⁰²² (т.к. нас интересуют положительные корни, мы можем это сделать). Тогда: 1=a₂/x+a₃/x²+...+a₂₀₂₃/x²⁰²². Что мы можем сказать про функцию, стоящую справа?

Подсказка 5

Она строго убывает. Действительно, при увеличении x знаменатель каждой дроби увеличится, а значит, сами они уменьшатся. ⇒ Справа функция монотонно убывает, а слева константа, равная 1 ⇒ она пересекает ее не более чем в 1 точке. Победа!

Показать ответ и решение

Докажем, что это невозможно.

От исходного уравнения перейдем к уравнению, в котором коэффициенты многочлена образуют произвольную перестановку $(a2,a3,...,a2023)$ из чисел ${2,3,...,2023}:$

2022 2021 2020 x − a2x − a3x − ...− a2022x− a2023 = 0

Заметим, что $x= 0$ не является корнем уравнения, т.к. при его подстановке в уравнение получим:

− a2023 =0,

что неверно.

Перенесём все отрицательные члены направо, а затем поделим уравнение на $x2022$ (при условии $x⁄= 0$ ):

x2022 = a2x2021+a3x2020+ ...+ a2022x +a2023

1= a2+ a32 + ...+ a22020221 + a22002322 x x x x

В правой части уравнения получили строго монотонно убывающую на положительной полуоси функцию:

f(x)= 20∑22ak+1 k=1 xk

Доказательство строгой монотонности: пусть $x1 > 0,x2 > 0,x1 <x2.$ Тогда для любого $k ∈{1,2,...,2022}$ выполнено:

ak+k1< ak+k1⇒ f(x2)< f(x1) x2 x1

Строгое монотонное убывание $f(x)$ на положительной полуоси означает, что она пересекает горизонтальную прямую $y = 1$ в единственной точке, которая и будет единственным положительным корнем исходного уравнения.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 4#71017

Две сферы касаются друг друга внешним образом и каждая из них касается внутренним образом большей сферы. Радиус одной в два раза, а другой — в три раза меньше радиуса наибольшей сферы. В точке касания малых сфер друг с другом построена касательная плоскость к ним. Найдите расстояние от этой плоскости до центра наибольшей сферы, если ее радиус равен $R.$

Источники: Надежда энергетики-2023, 11.4 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Не очень удобно работать в пространстве. Может, тогда перейти в плоскость? Давайте перейдем в плоскость α, проходящую через центры наших сфер...

Подсказка 2

Обозначим их центры за O, O₁ и O₂. Пускай R=6r ⇒ радиусы оставшихся двух сфер равны 3r и 2r ⇒ O₁O₂=5r, OO₁=3r и OO₂=4r. Что мы можем сказать про треугольник △O₁OO₂?

Подсказка 3

Верно, он прямоугольный! Пускай плоскость β, касающаяся наших сфер, пересекает α по прямой L. Обозначим за K- точку пересечения OO₂ и L, D- основание перпендикуляра из O на прямую L и F- точку касания маленьких сфер. Какие между собой треугольники △ODK, △KFO₂ и △O₁OO₂?

Подсказка 4

В яблочко, они подобны! Тогда: KO₂/FO₂=O₁O₂/OO₂ ⇒ KO₂=r*5/2 ⇒ KO=r*3/2. Также: OD/KO=OO₂/O₁O₂ ⇒ OD=r*6/5=R/5.

Показать ответ и решение

Проведём сечение описанной композиции плоскостью, проходящей через центры трех сфер. Искомое расстояние будет длиной отрезка $OD$ на этой плоскости.

$PIC$

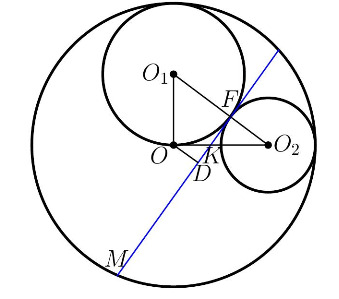
Пусть радиусы малых окружностей равны $2r$ и $3r.$ Тогда радиус наибольшей (внешней) равен $6r$ (дано: $6r= R$ ). Рассмотрим $△O1OO2.$ Его стороны равны $3r,4r$ и $5r,$ следовательно, он прямоугольный.

Обозначим точку пересечения искомой хорды с отрезком $O1O2$ через $F,$ а с отрезком $OO2$ через $K.$ Опустим из центра наибольшей окружности перпендикуляр $OD$ на искомую хорду (отрезок общей касательной). Тогда искомая хорда делится точкой $D$ пополам и перпендикулярна отрезкам $OD$ и $O1O2.$

Прямоугольные треугольники $O1OO2,KFO2,KDO$ подобны. Поэтому $KO O O F-O2= -O1O-2 2 2$ , откуда $5 KO2 = 2r$ и $3 KO = 2r.$

Далее, $OD- OO2-- KO = O1O2,$ откуда $6 1 OD = 5r= 5R.$

Ответ: 0,2 R

Ошибка.
Попробуйте повторить позже

Задача 5#71018

Какое число больше: $20232023$ или $20222024?$

Источники: Надежда энергетики-2023, 11.5 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Есть два способа определить какое из двух чисел больше. Можно вычесть одно из второго и посмотреть на знак, а можно найти отношение первого ко второму и посмотреть больше оно единицы или меньше. Очевидно, что вычитание в этой задаче нам ничего не даст, поэтому давайте найдем отношение.

Подсказка 2

Подумайте, как стоит расписать полученное отношение, чтобы воспользоваться тем, что для всех натуральных k выполняется неравенство 2 <= (1 + 1/k)^k < 3

Показать ответ и решение

Рассмотрим отношение чисел

20232023 2023 ( 2023)2022 2023 ( 1 )2022 20222024 = 20222-⋅ 2022 = 20222 ⋅ 1 +2022

Применим известное неравенство:

( ) 2 < 1+ 1 k < 3 ∀k ∈ℕ, k> 1 k

Тогда

2023 ( 1 )2022 2023⋅3 20222 ⋅ 1+ 2022 < 2022-⋅2022 < 1

_________________________________________________________________________________________________________________________________________________________________________________

Замечание.

Известное неравенство принималось на олимпиаде без док-ва, но любые корректные попытки его обоснования поощрялись. Покажем, как его можно доказать с помощью формулы бинома Ньютона:

( ) 1 +-1 k = 1+ n-⋅ 1+ n(n−-1)⋅ 1-+ n(n−-1)(n−-2)-⋅ 1-+ ...+ n!⋅ 1-= k 1! n 2! n2 3! n3 n! nn

1- ( 1) -1 ( 1) ( 2) 1-( 1) ( n−-1) = 2+ 2! ⋅ 1− n +3! ⋅ 1− n 1− n + ...+ n! 1− n ⋅...⋅ 1− n

Видно, что все скобки вида $( k) 1+ n$ меньше 1, но при этом больше 0. Значит, если заменим их на 1, то выражение от этого увеличиться.

( ) ( )( ) ( ) ( ) 2+ 1-⋅ 1− 1 + 1-⋅ 1− 1 1 −-2 + ...+ 1- 1− 1 ⋅...⋅ 1− n−-1 < 2! n 3! n n n! n n

<2 + 1--+ --1--+ ...+ ---1----< 2+ 1 +-1 +...+--1- 1⋅2 1⋅2⋅3 1⋅2⋅...⋅n 2 22 2n−1

Последнее неравенство верно, ведь мы просто заменили в числителях все числа, которые больше 2, на 2, тем самым уменьшили знаменатели, следовательно, увеличили значение выражения.

1 -1 --1- 1 -1 --1- -1 1 -1-- 2+ 2 + 22 + ...+ 2n−1 < 2+ 2 +22 +...+ 2n−1 + 2n +...=2 +2 ⋅1− 12 = 3

В конце мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии.

Ответ:

$20222024$