Тема Звезда - задания по годам

Звезда 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела звезда - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#74588

Известно, что

3b> 9a +c> 0

Докажите, что

b2 > 4ac

Источники: Звезда - 2022 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Давайте внимательно посмотрим на неравенство, которое нужно доказать. Где такое выражение чаще всего встречается? Попробуйте подумать в этом направлении.

Подсказка 2

Верно, это дискриминант квадратного трёхчлена с нужными коэффициентами. Тогда давайте рассмотрим трёхчлен ax^2 + bx +c. Как теперь можно переформулировать нашу задачу?

Подсказка 3

Ага, когда наше неравенство будет выполняться, многочлен будет иметь два корня. Тогда нужно просто проанализировать знаки трёхчлена в хороших точках. Какие это могут быть точки, учитывая неравенства, данные по условию?

Подсказка 4

Верно, попробуйте подставить точки 3 и -3 и посмотреть на знаки трёхчлена. Но не забудьте ещё проверить a=0, потому что в этом случае у вас не квадратный трёхчлен. В таком решении это важно.

Показать доказательство

Первое решение.

9a +c 2 (9a+ c)2 3b> 9a+ c> 0 ⇐⇒ b> -3--->0 =⇒ b > ---9---

Чтобы доказать $2 b > 4ac,$ хочется доказать $(9a+c)2 --9--≥ 4ac.$ Преобразуем это неравенство:

81a2 +18ac+c2 ≥ 36ac

2 2 81a − 18ac+c ≥ 0

(9a− c)2 ≥0

Верно, поэтому было верным и

2 b2 > (9a-+c)-≥ 4ac 9

Значит, $b2 >4ac.$

Второе решение.

Нам нужно доказать, что $b2− 4ac> 0,$ а это очень напоминает дискриминант, поэтому давайте придумаем квадратный трёхчлен с таким дискриминантом и докажем, что он имеет 2 корня. Очевидно, подходит $f(x)= ax2+bx+ c.$ Всегда ли мы можем рассматривать его дискриминант? Нет, в случае $a =0$ никакого дискриминанта нет, поэтому его надо рассмотреть отдельно — благо, тут всё просто и понятно, $3b> 0 =⇒ b2 > 0,$ а $4ac= 0,$ значит, $b2 >0 =4ac.$

Теперь рассмотрим случай, когда $a ⁄=0.$ В неравенстве из условия было $3b,$ поэтому давайте попробуем подставить 3 и -3.

f(3)= 9a+ 3b+c> 0, так как 3b> 0 и 9a+c >0

f(−3)= 9a − 3b+ c< 0, так как 3b>9a+ c

То есть квадратный трёхчлен принимает положительные и отрицательные значения, а значит, он имеет 2 корня! И его $D = b2 − 4ac> 0.$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#74590

Решите систему уравнений

{ sin3x+ sin4y = 1, 3 5 cos x+ cos y = 1.

Источники: Звезда - 2022 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Наши выражения как-то подозрительно напоминают основное тригонометрическое тождество. Только вот у нас sin не складывается с cos, да и степени не те... Давайте хотя бы сделаем первое условие, для этого сложим два уравнения...

Подсказка 2

Имеем, что sin³x+sin⁴x+cos³y+cos⁵y = 2. С другой стороны, 2 = sin²x+cos²x+sin²y+cos²y. Как из этого получить интересное неравенство...

Подсказка 3

Т.к. sinⁿx ≤ sin²x и cosⁿx ≤ cos²x, при n ≥ 3, то 2 = sin³x+sin⁴x+cos³y+cos⁵y ≤ sin²x+sin²x+cos²y+cos²y = 2. Значит все неравенства обращаются в равенства. Решите получившуюся систему и радуйтесь жизни!

Показать ответ и решение

Сложим два уравнения системы, тем самым получим новое уравнение, являющееся следствием системы.

3 4 3 5 sin x+ sin y+ cos x+ cos y = 2

Воспользуемся ОТТ:

3 4 3 5 2 2 2 2 sin x +sin y +cosx +cos y = sin x+cos x+ sin y+ cos y

sin2x(sinx − 1)+ cos2x(cosx− 1)+sin2y(sin2y− 1)+cos2y(cos2y− 1)= 0

Квадраты неотрицательные, а все скобочки $≤ 0,$ тогда, чтобы сумма была = 0, каждое слагаемое должно быть равно 0. Имеем систему:

( ||| sin2 x(sinx − 1)= 0 |{ cos2x(cosx− 1)= 0 ||| sin2 y(sin2y− 1)= 0 |( cos2y(cos2y − 1)= 0

Решим для $x :$

Из первого уравнения возможны 2 случая:

1) $sinx= 0.$ Тогда из второго $cosx= 1 =⇒ x= 2πk,k∈ ℤ$

2) $sinx= 1.$ Тогда $cosx= 0 =⇒ x = π+ 2πn,n ∈ℤ 2$

Решим для $y :$

1) $siny = 0,$ тогда $2 cos y = 1 =⇒ cosy = ±1 =⇒ y = πm,m ∈ℤ$

2) $2 sin y = 1 =⇒ sin y = ±1,$ тогда $π cosy = 0,y = 2 + πt,t∈ ℤ$

И так как мы изначально получили следствие из исходной системы, надо не забыть проверить, какие серии корней подходят, а какие нет, подставив в изначальную систему все комбинации возможных значений $sinx,cosx,siny,cosy.$

Подходят следующие варианты:

1) $π x= 2πk,y = 2 +2πt,$ $k,t∈ ℤ$

2) $π x= 2 + 2πn,y =2πm,$ $n,m ∈ ℤ$

Ответ:

$(2πk,π+ 2πt),(π +2πn,2πm),k,n,m,t∈ℤ 2 2$

Ошибка.
Попробуйте повторить позже

Задача 3#74591

Плоскость, параллельная основанию $ABC$ пирамиды $MABC$ , отсекает пирамиду $MA B C 1 1 1$ (вершины $A ,B ,C 1 1 1$ расположены на рёбрах $MA,MB, MC$ соответственно). Объём пирамиды $MABC$ равен 375 , объём пирамиды $MA1B1C1$ равен 81. Найдите объём пирамиды $MAB1C1$ .

Источники: Звезда - 2022 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Т.к. плоскости (A₁B₁C₁) и (ABC) параллельны, то MA₁/MA=MB₁/MB=MC₁/MC=k. Тогда объемы тетраэдров MA₁B₁C₁ и MABC относятся как коэффициент подобия k в кубе. Чему же равен k?

Подсказка 2

Верно, 3/5! Мы видим, что объем тетраэдра MAB₁C₁ состоит из объемов тетраэдров MA₁B₁C₁ и AA₁B₁C₁, у которых есть общее основание. Как же тогда относятся их объемы...

Подсказка 3

Они относятся как высоты, которые, в свою очередь, относятся как MA₁/A₁A=3/2. Посчитайте объем AA₁B₁C₁ и завершите решение!

Показать ответ и решение

$PIC$

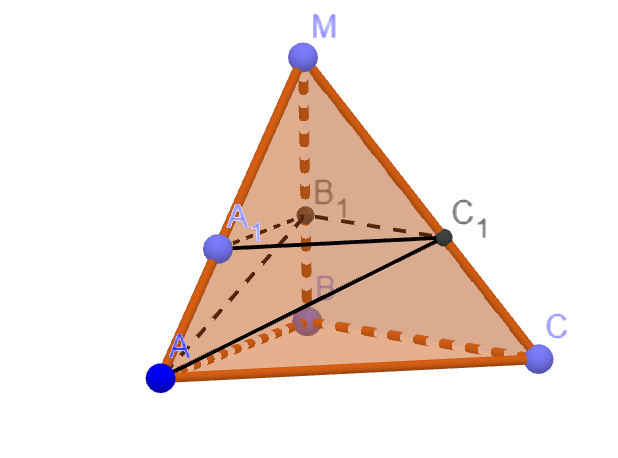
Так как плоскость $(A1B1C1)$ параллельна плоскости основания $ABC,$ то

MA1-= MB1- = MC1 = k MA MB MC

Пирамиды $MA1B1C1$ и $MABC$ подобны, тогда их объёмы относятся как коэффициент подобия $k$ в кубе:

VMA1B1C1 = 81-= 27-=k3 =⇒ k= 3 VMABC 375 125 5

Пусть $MA =3x, 1$ тогда $A A= 2x. 1$ Заметим, что объём пирамиды $MAB C 1 1$ складывается из двух кусочков: $MA B C , 1 1 1$ объём которой мы знаем, и $AA1B1C1.$ Причём эти 2 пирамиды имеют общее основание $A1B1C1,$ тогда их объёмы относятся так же, как относятся их высоты к $(A1B1C1).$ А высоты относятся так же, как относятся $MA1$ и $AA1,$ то есть высота пирамиды $MA1B1C1$ больше высоты пирамиды $AA1B1C1$ в $MA1- 3x- 3 AA1 = 2x = 2.$ Значит,

VAA1B1C1 2 2 VMA1B1C1 = 3 =⇒ VAA1B1C1 = 3 ⋅81= 54

VMAB1C1 =VMA1B1C1 +VAA1B1C1 = 81+ 54 =135

Ответ: 135

Ошибка.
Попробуйте повторить позже

Задача 4#74600

Датчик случайных чисел за одно действие уменьшает или увеличивает на 1 коэффициент перед $x$ или свободный член в квадратном трёхчлене. После некоторого числа таких операций он преобразовал трёхчлен $2 x − 20x+22$ в трехчлен $2 x − 202x +2$ . Верно ли, что среди полученных в процессе квадратных трёхчленов есть такой, у которого целые корни? Ответ обоснуйте.

Источники: Звезда - 2022 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Следить сразу за двумя целыми корнями как-то сложновато. Давайте для начала попробуем доказать, что в какой-то момент будет один целый корень. Может возьмем какой-нибудь конкретный?

Подсказка 2

А чего мелочится, давайте посмотрим на 1! Если у нашего трехчлена есть корень 1, то сумма его коэффициентов равна 0. Как меняется сумма наших коэффициентов после одной операции?

Подсказка 3

Верно, она меняется на 1! Изначально сумма была 3, а в конце -199. Значит в какой-то момент она станет равной 0. Итак, в какой-то момент у нашего трехчлена будет корень 1. Докажите, что тогда у него есть второй целый корень (возможно кратный)!

Показать ответ и решение

Давайте попробуем доказать, что в какой-то момент у квадратного трёхчлена будут целые корни. Для этого угадаем один из них. Если сумма коэффициентов многочлена равна 0, то есть корень $x =1.$ У начального многочлена $2 f1(x)= x − 20x+ 22$ сумма коэффициентов равна 3, а у конечного $2 f2(x)=x − 202x +2$ сумма коэффициентов равна -199, при этом за одно действие ровно один из коэффициентов меняется на 1, значит, сумма коэффициентов меняется на 1. Но если она была положительной, а потом стала отрицательной, то в какой-то момент обязательно была равна 0. То есть в какой-то момент у нас был трёхчлен $2 f(x)= x +bx+ c$ , один из корней которого равен 1! А по теореме Виета второй корень равен $c$ — тоже целому числу $=⇒$ у трёхчлена 2 целых корня!

Ответ: да