Тема Звезда - задания по годам

Звезда 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела звезда - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83740

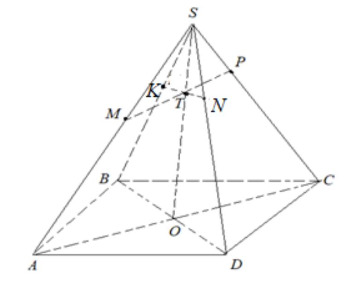
Параллелограмм $ABCD$ является основанием пирамиды $SABCD.$ Точки $M,N$ и $P$ лежат на рёбрах $SA,SD$ и $SC$ соответственно, причём

SM :MA = 1:2, SN :ND = 1:3, SP :PC =1 :4

В каком отношении плоскость $MNP$ делит ребро $SB?$

Источники: Звезда - 2024, 11.1 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Построить точку пересечения плоскости MNP и ребра SB сразу так сложно. Кажется, не хватает какой-нибудь точки на MP, чтобы провести через неё и N прямую, пересекающую ребро SB в искомой точке (пусть K).

Подсказка 2

Да это же точка, получаемая пересечение MP и SO, где SO — пересечение плоскостей BSD и ASC, назовём её Т. Точку ввели, а как она делит SO — не узнали. А хотелось бы, потому что её можно рассмотреть и для △ASC (а мы знаем про то как делят его стороны M и P), и для △BSD (содержащий интересующую нас точку K).

Подсказка 3

Отношение ST : NO можно найти, рассмотрев △ASC. А ещё же у нас есть отношение AO : OC (подумайте, чем является точка O для основания). Часто, когда мы видим отношения отрезков, хочется применить теорему Фалеса, только вот нам не хватает несколько параллельных прямых... Какие можно провести, чтобы использовать оба упомянутых отношения на сторонах SA и AC?

Подсказка 4

В предыдущей подсказке попробуйте провести прямые из A и O параллельно MP. С помощью теоремы Фалеса можно найти отношение ST : NO. Если Вы всё правильно посчитали, то не составит труда, используя уже упомянутую теорему, найти отношение SK : KB.

Показать ответ и решение

Пусть плоскости $BSD$ и $ASC$ пересекаются по прямой $SO.$ Рассмотрим треугольник $ASC.$ Пусть $T = MP ∩ SO.$

$PIC$

В треугольнике $ASC$ проведём прямые $AL$ и $OQ$ параллельные $MP.$

$PIC$

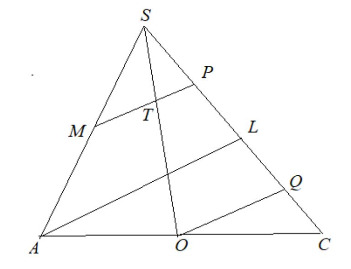
По теореме Фалеса имеем

SPPL-= SMMA- = 12, LQQC-= AOOC- =1

Учитывая, что $SP :PC =1 :4,$ получаем, что

ST-= 1 TO 3

Пусть $K = NT ∩ SB.$ Так как

SN :ND = ST :TO =1 :3,

то в силу теоремы Фалеса прямые $BD$ и $NK$ параллельны, и, следовательно,

SK :KB =1 :3

Ответ: 1:3

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#83741

Решите систему

(| log3x⋅log4y 1 ||||| log2(xy) = 3 ||{ log3y⋅log25z 3 || --log5(yz)- = 5 ||||| log z⋅logx |( --l27og16(zx2)- = 1

Источники: Звезда - 2024, 11.2 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Кажется, от дробей здесь нет пользы, они только пугают. Может, избавится от них? Только не забудьте про ОДЗ!

Подсказка 2

Получается как-то очень много одинаковых логарифмов. Когда много одинакового, то на помощь приходит замена.

Подсказка 3

Система из трёх не очень страшных уравнений, можно и подстановкой попробовать решить. Но не забывайте проверять решения на ОДЗ!

Показать ответ и решение

Запишем ОДЗ:

(| x> 0 ||||| y > 0 |||{ | z > 0 ||||| xy ⁄= 1 |||( yz ⁄= 1 zx⁄= 1

Преобразуем систему к виду

(|| 3log x⋅log y = 2log (xy) |{ 3 2 2 ||| 5log3y⋅log5z = 6log5(yz) ( 4log3z⋅log2x= 3log2(zx)

Используем формулу перехода к новому основанию и формулу логарифма произведения

( |||| 3log3x ⋅ lologg3y2 = 2loglo3g(xy2) ||||{ 3 3 5log3y⋅ log3z= 6log3(yz) ||||| log35 log35 |||( 4log3z⋅ log3x= 3log3(zx) log32 log32

(|| 3log x⋅log y = 2log (xy) |{ 3 3 3 ||| 5log3y⋅log3z = 6log3(yz) ( 4log3z⋅log3x= 3log3(zx)

( |||{ 3log3 x⋅log3y = 2log3x+ log3y | 5log3 y⋅log3z = 6log3y+ log3z ||( 4log3 z⋅log3x= 3log3z+ log3x

Сделаем замену: $log3x= u,log3y = v,log3z =t,$ получаем систему

( |{ 3u⋅v = 2(u+v) | 5v⋅t= 6(v+ t) ( 4t⋅u= 3(u +t)

Из первого уравнения системы выразим

v = -2u-- 3u− 2

Из третьего уравнения выразим

-3u-- t= 4u − 3

Подставим во второе уравнение системы, получим после преобразований уравнение

u2− u =0

При $u =0$ получаем $v = t= 0,$ но соответствующие значения $x,y,z$ не удовлетворяют ОДЗ. При $u =1$ получаем $v = 2,t=3,$ следовательно, $x= 3,y =9,z = 27.$

Ответ:

$(3,9,27)$

Ошибка.
Попробуйте повторить позже

Задача 3#83742

Даны числа $x,y,z$ такие, что

x 4 6 4 + sin y+ ln z = 16

Докажите, что

x+1 2 3 2 + 3sin y− 6ln z ≤ 28

Источники: Звезда - 2024, 11.3 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Тригонометрия, логарифм и показательная функция в одном месте — вряд ли мы здесь обойдёмся банальными преобразованиями. Видно только, что первое выражение, равное 16, — сумма трёх квадратов каких-то величин, а во втором выражении стоят похожие величины, но без квадратов. Какие есть неравенства, связывающие такие суммы?

Подсказка 2

Неравенство Коваля-Белова-Шурыгина! Ой, то есть Коши-Буняковского-Шварца) Ну то самое про квадрат суммы и сумму квадратов. Говоря по простому, это факт, что скалярное произведение не больше произведения длин (это же и так понятно, да?..) Давайте соорудим векторы с нужными координатами!

Подсказка 3

Компоненты первого вектора — величины, сумма квадратов которых равна 16. А второй вектор нужно подобрать так, чтобы их скалярное произведение выглядело как то выражение, которое не должно превосходить 28. Пробуйте!

Показать доказательство

Используем неравенство КБШ в векторном виде. Рассмотрим векторы $⃗a= (2x;sin2y;ln3z)$ и $⃗b= (2;3;−6).$ Скалярное произведение

x+1 2 3 ⃗a ⋅⃗b =2 + 3sin y− 6ln z ≤ |⃗a|⋅|⃗b|

Имеем

⃗ √-------- |b|= 4+ 9+ 36 =7

|⃗a|= ∘4x+-sin4y+-ln6z =4

Тогда получаем, что

2x+1+ 3sin2y− 6ln3z ≤ 28

Ошибка.
Попробуйте повторить позже

Задача 4#83743

Дана последовательность:

∘ ∘ n ∘ a1 = cos10 ,a2 =cos100,...,an = cos(10) ,...

Найдите наименьшее значение выражения

a1⋅cosx +(a2+ a2023+a2024)⋅sinx, где x∈ ℝ

Источники: Звезда - 2024, 11.4 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Даны косинусы углов в градусах. Мы же знаем, что косинус — периодичная функция с периодом 360 градусов. Попробуем заметить что-нибудь, связанное с периодичностью косинуса, про аргументы двух соседних членов последовательности, то есть 10^n и 10^(n+1).

Подсказка 2

После того, как мы поняли, что из себя представляют а_2023 и а_2024, осталось преобразовать выражение с x по известным тригонометрическим формулам. В этот момент уже будет понятно, как искать наименьшее значение, ведь тригонометрические функции принимают ограниченные значения.

Показать ответ и решение

Посмотрим на разность градусных мер углов у соседних членов последовательности: