Тема БИБН - задания по годам

БИБН 2025

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела бибн - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#103845

Решите уравнение $2cos4x− sin3x= 1$ .

Источники: БИБН - 2025, 11.1 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Неприятно, когда в уравнении есть и синус, и косинус. Давайте попробуем оставить что-то одно.

Подсказка 2

С помощью ОТТ выразим косинус через синус. При раскрытии скобок получатся большие степени, поэтому наша задача — разложить выражение на множители. Вспомните формулы разности квадратов и суммы кубов для этого.

Подсказка 3

Теперь нам остаётся только аккаратно раскрыть произведение в бОльшей скобке, и заново всё сгруппировать, чтобы найти корни:)

Показать ответ и решение

По основному тригонометрическому тождеству уравнение равносильно

2 2 3 2(1− sinx) − sin x= 1

2 2 2 2(1− sinx) (1+ sinx) = (1 +sinx)(1− sinx+ sin x)

$sinx= −1$ либо

2(1+ sinx)(1− 2sinx+ sin2x)= 1− sinx+ sin2x

2− 4sinx +2sin2x +2sin x− 4sin2x+ 2sin3x= 1− sinx+ sin2x

1− sinx− 3sin2x+ 2sin3x= 0

1− 2sinx+ sinx− 2sin2x− sin2x+ 2sin3x =0

2 (1− 2sinx)(1+ sinx − sin x)= 0

$sinx= 1 2$ либо $sinx = −1±-√1+4. −2$

В итоге после объединения решений с учётом области значений синуса подходят $1 1−√5 − 1;2; 2 .$ Соответственно

⌊ x= − π + 2πn,n∈ ℤ | π 2 ||| x= 65π+2πn,n∈ ℤ || x= 6 + 2π1−n√,n5-∈ℤ ⌈ x= arcsin 2 1−+√25πn,n∈ ℤ x= π− arcsin 2 +2πn,n∈ ℤ

Ответ:

$π π 5π 1-− √5 1−√5- − 2 + 2πn;6 + 2πn; 6 +2πn;arcsin 2 + 2πn;π− arcsin 2 + 2πn; n∈ ℤ$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#103846

Дан прямоугольный треугольник $ABC$ ( $C$ — вершина прямого угла) с острым углом $α$ при вершине $A.$ Две окружности с центрами $O1$ и $O2$ проходят через вершины $A,C$ и $B,C$ соответственно и касаются прямой $AB$ . Найдите отношение площадей треугольников $ABC$ и $O1MO2$ , где $M$ — середина гипотенузы $AB$ .

Источники: БИБН - 2025, 11.2 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Давайте будем постепенно "раскручивать" то, что дано в условии. O₁ и O₂ центры окружностей, как тогда можно их связать с M?

Подсказка 2

Каким является треугольник O₁MO₂?

Подсказка 3

Отлично, O₁MO₂ — прямоугольный! А чему равно отношение площадей прямоугольных треугольников?

Подсказка 4

Нужное нам отношение равно отношению произведений катетов! Осталось лишь понять, как используя данный угол выразить одни катеты через другие ;) Не забываем, что на картинке много прямых углов!

Показать ответ и решение

$PIC$

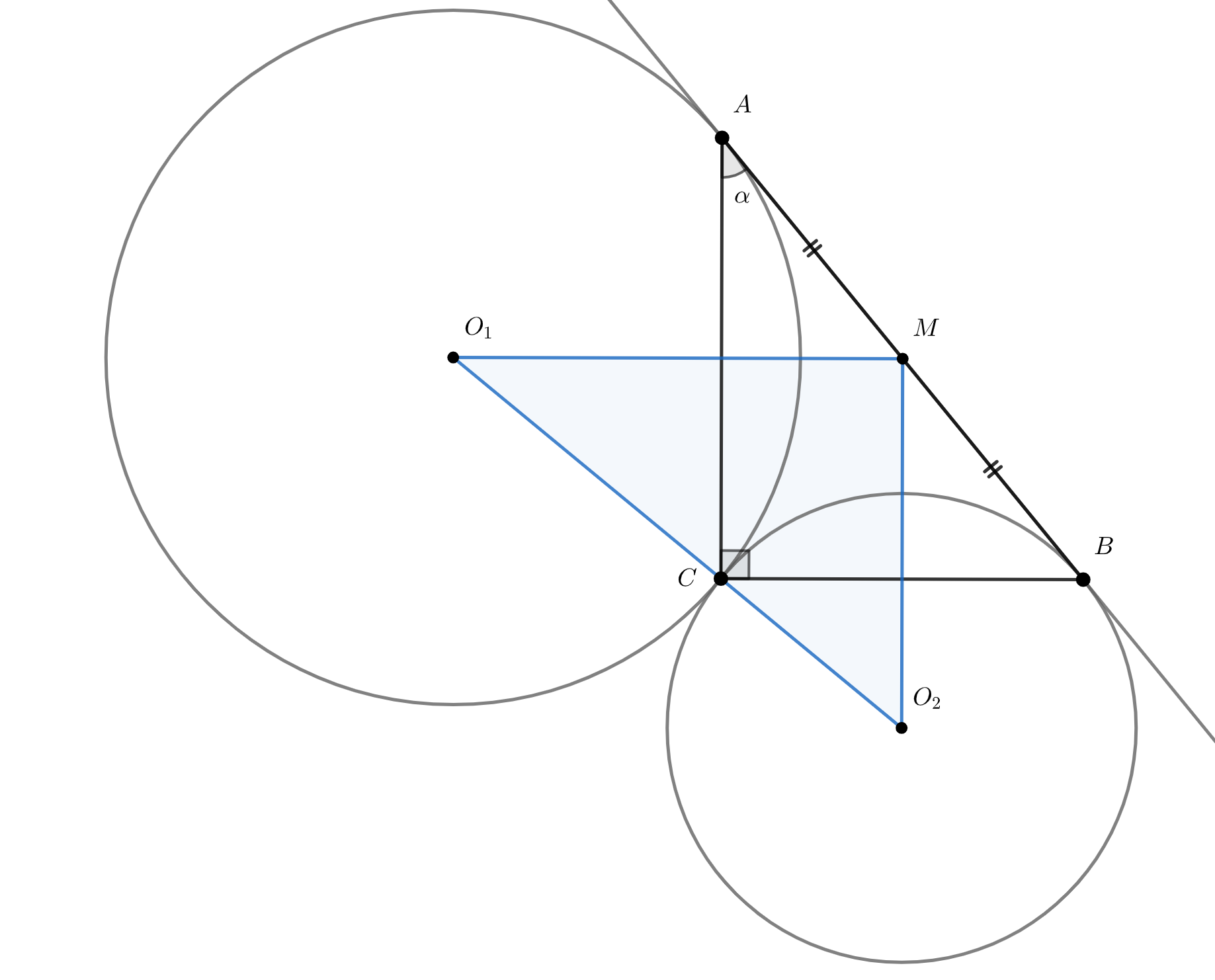
Как центры описанных окружностей, точки $O1$ и $O2$ лежат на серединных перпендикулярах к $AC$ и $BC$ соответственно, причём пересечением перпендикуляров является точка $M.$ Так как $AC$ и $BC$ взаимноперпендикулярны, то и серединные перпендикуляры $O1M, O2M$ к ним тоже взаимноперпендикулярны. Поэтому треугольник $O1MO2$ — прямоугольный с прямым углом при вершине $M.$

$PIC$

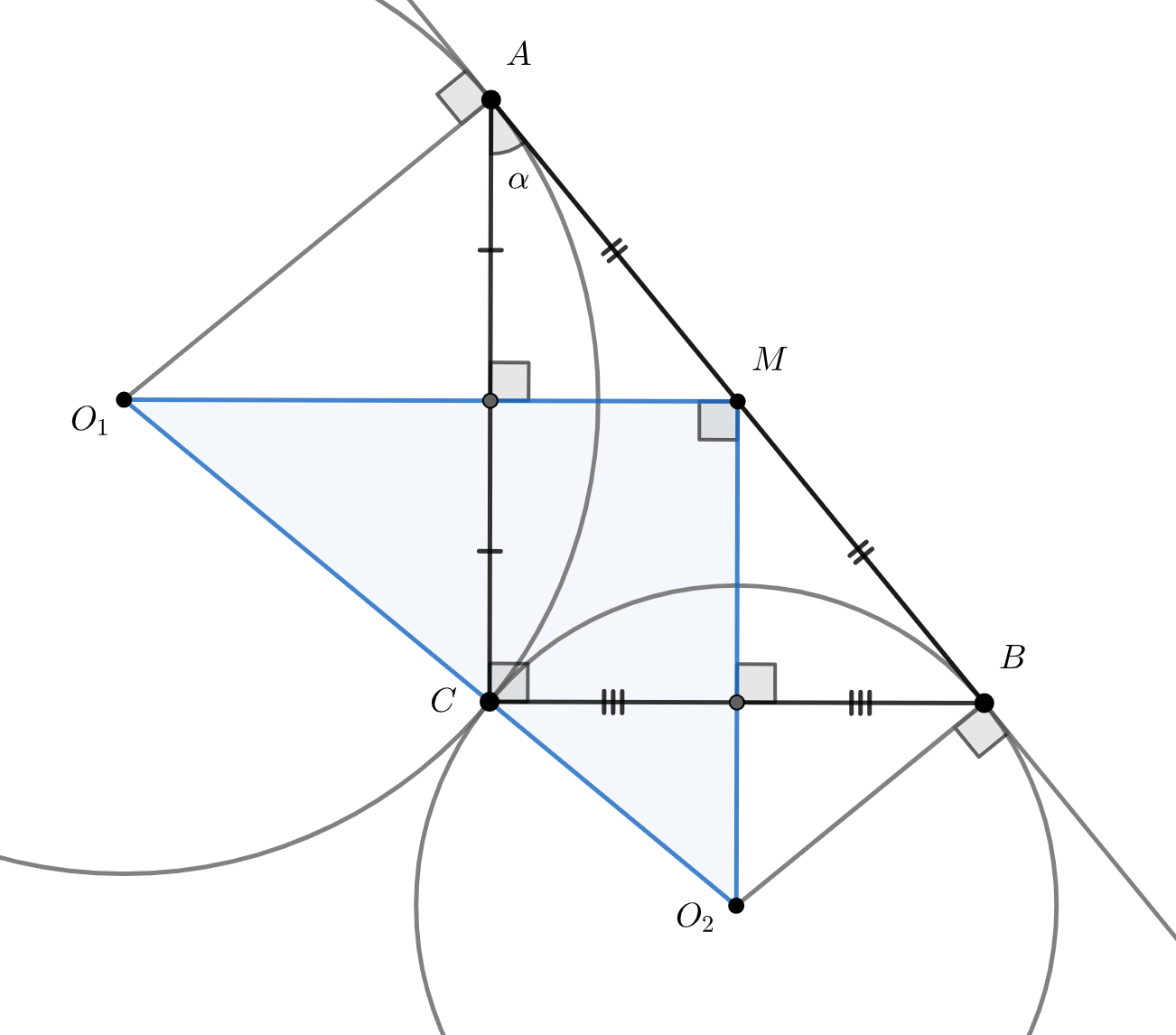
Отношение площадей прямоугольных треугольников равно отношению произведений их катетов, то есть

-SABC--= -AC-⋅BC--- SO1MO2 O1M ⋅MO2

По условию окружности касаются $AB,$ поэтому радиусы $O1A$ и $O2B$ перпендикулярны касательной $AB.$ Тогда из соответствующих прямоугольных треугольников

AM AB MB AB O1M = sinα-= 2sinα-; O2M = cosα-= 2cosα

В итоге

-AC-⋅BC--= AC-⋅BC-⋅2sinα⋅2cosα O1M ⋅MO2 AB ⋅AB

Так как $AC = AB cosα,BC =AB sinα,$ окончательно получаем

4sin2α cos2α= sin22α

Ответ:

$sin22α$

Ошибка.
Попробуйте повторить позже

Задача 3#103847

Для данного треугольника $ABC$ с соответствующими сторонами $a,b,c$ рассматривают уравнение $ax4+ bx= c$ . Докажите, что у этого уравнения ровно два корня, они разных знаков, причём отрицательный корень по модулю больше положительного.

Источники: БИБН - 2025, 11.3 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

В задаче уравнение, у которого корни искать неприятно... но их можно изобразить! Какой графический смысл у корней?

Подсказка 2

Корни — это пересечения графиков! Поэтому имеет смысл изобразить параболу и прямую, у которых мы хотим найти пересечения!

Подсказка 3

Изобразите графики y = ax⁴, y = c - bx и найдите их пересечения — это и будут корни.

Подсказка 4

Для доказательства неравенства модулей используйте подобие треугольников ;)

Показать доказательство

Так как $a,b,c$ являются сторонами треугольника, то они положительны. Поэтому $y = ax4$ это парабола 4 степени ветвями вверх, а $y =c− bx$ это прямая с отрицательным угловым коэффициентом, которая проходит через точки $(0;c)$ и $c (b;0).$ Нарисуем графики:

$PIC$

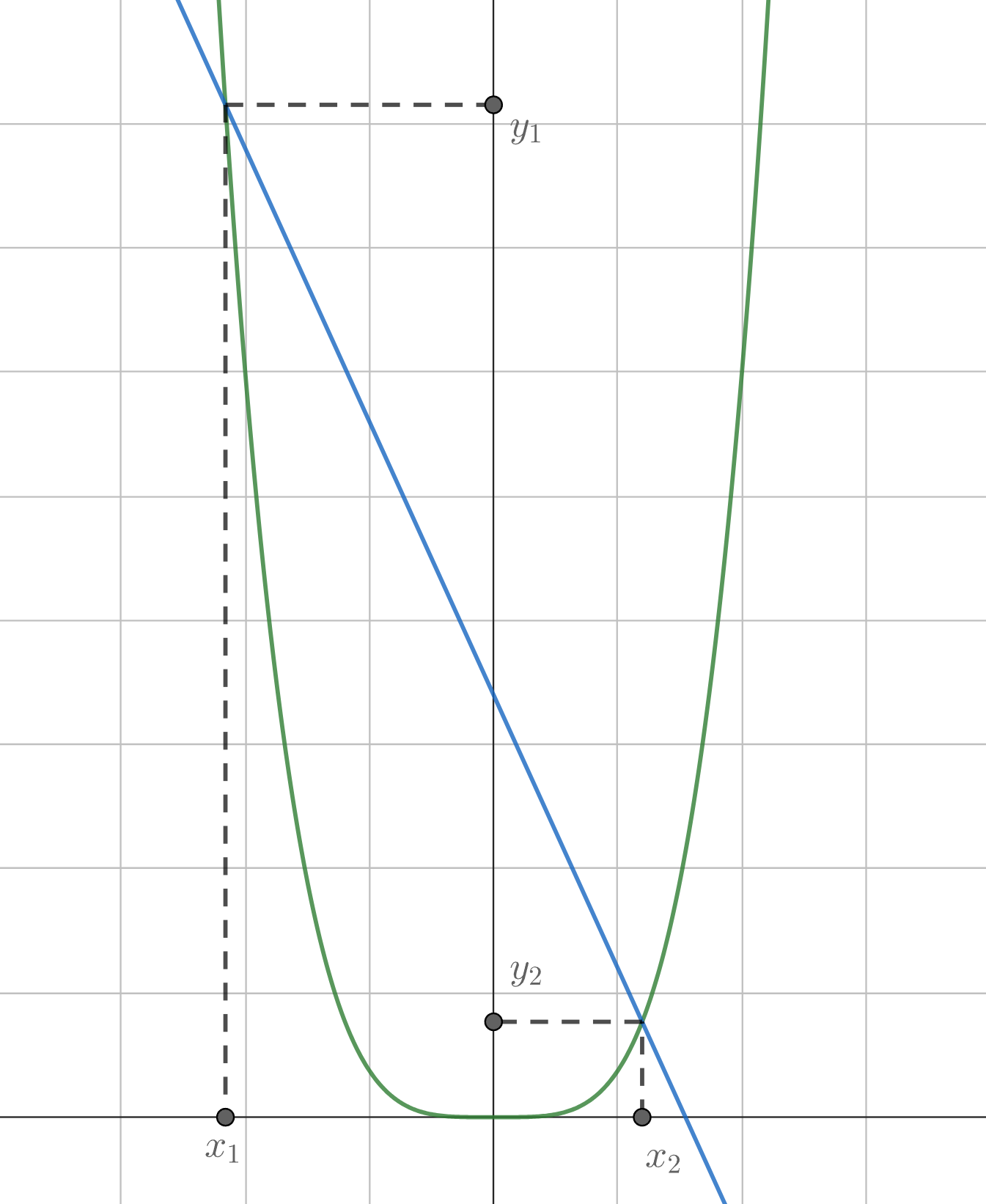
Очевидно, что две данные функции имеют две точки пересечения. Обозначим их абсциссы за $x1 < 0< x2$ (уже очевидно из графика, что корни разных знаков), а ординаты за $y1$ и $y2.$ Из подобных прямоугольных треугольников видно, что $y1 > y2,$ поэтому

1√ -- 1√-- |x1|= a 4y1 < a 4y2 = |x2|

Ошибка.
Попробуйте повторить позже

Задача 4#103848

а) Определите количество положительных корней уравнения $9⋅x6x = 1$ ;

б) есть ли у этого уравнения отрицательные корни?

Источники: БИБН - 2025, 11.4 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1, пункт а

Как можно преобразовать степень x, чтобы получилось прямо его выразить?

Подсказка 2, пункт а

Запишите степень x как степень e. Тогда можно будет воспользоваться свойствами логарифма и "выдвинуть" x :)

Подсказка 3, пункт а

Отлично, теперь мы знаем, какому числу равен xln(x). Осталось лишь понять, когда же такая функция принимает конкретное значение ;) А для этого нужно её исследовать!

Подсказка 1, пункт б

Попробуйте подставить какие-то отрицательные значения и посмотреть, а можно ли так делать.

Показать ответ и решение

а) По основному логарифмическому тождеству уравнение равносильно

6xlnx 9e = 1

6xlnx =ln1 9

1 1 x lnx= 3 ln 3

Производная функции $y(x)= xlnx$ равна $1 lnx+ xx =lnx+ 1,$ поэтому функция убывает при $1 lnx≤ −1 ⇐⇒ 0< x≤ e$ и возрастает при $1 x≥ e.$

В точке минимума значение функции равно $1 1 1 e ⋅(−1)< 3ln3,$ так как $− 3= −3lne< −3ln3< −eln3,$ поэтому функция достигает значение $1 1 3ln 3$ по одному разу левее и правее точки минимума (для обоснования стоит ещё упомянуть непрерывность функции и её неограниченность слева и справа от точки минимума);

б) возведение произвольного отрицательного числа в произвольную отрицательную степень не имеет смысла (не определено однозначно), потому что нарушаются свойства степеней. Например, $(−1)−1 = −11 =− 1,$ но при этом $( )−1 −1 (−1)−1 = (−1)2 2 =1 2 = 1√1 = 1.$

Ответ:

а) 2;

б) нет

Ошибка.
Попробуйте повторить позже

Задача 5#103849

Дан выпуклый $n$ -угольник $A A ...A 1 2 n$ и точка $M$ на плоскости. Пусть $M i$ — проекция $M$ на прямую $A A i i+1$ (где $A = A n+1 1$ ). Докажите, что если выполняется равенство

( 2 2 2) 2 2 2 4 A1M1 +A2M 2 + ...+ AnM n =A1A 2+A2A 3+...+AnA 1,

то около $n$ -угольника можно описать окружность.

Источники: БИБН - 2025, 11.5 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Задача необычная, что делать? Мы видим, что суммируются не просто длины отрезков, а их квадраты, а еще и проекции есть, это наталкивает на какие-то воспоминания))

Подсказка 2

Конечно, здесь точно пригодится теорема Пифагора! Причем рассмотреть теорему лучше и для квадрата катетов A_i M_i, так и для A_{i+1}M_i, тогда после суммирования для каждой вершины многоугольника аналогичных равенств получим что-то интересное.

Подсказка 3

Теперь подумаем, что можем сказать в случае, если M_i лежит на отрезке A_i A_{i+1} или вне его? Как мы можем сравнить квадраты отрезков — поможет неравенство о средних, осталось опять просуммировать все неравенства!

Подсказка 4

Получается, мы доказали, что всегда выполняется неравенство, а в условии нам дано равенство! Остался один шаг: вспомнить, чем является центр описанной окружности.

Показать доказательство

Для любого $i$ от $1$ до $n$ по теореме Пифагора $A M2= A M2 − MM2 , i i i i$ при этом $A M2 i+1 i$ аналогично равно $A M2 − MM2 . i+1 i$ Поэтому

2 2 2 2 2 2 A1M1 +A2M 2 + ...+ AnM n = A2M1 +A3M 2 + ...+ A1Mn

При этом

2 2 2 2(AiMi +MiA i+1)≥ AiA i+1,

потому что в случае нахождения точки $Mi$ вне отрезка $AiAi+1$ очевидно даже более сильное $AiM2 + MiA2 > AiA2 , i i+1 i+1$ а в случае нахождения точки внутри отрезка $AiAi+1 = AiMi+ MiAi+1,$ поэтому по неравенству о средних для двух чисел

2 2 2 2 2 2 2 AiAi+1 =AiM i + MiAi+1 +2AiMi⋅MiAi+1 ≤ AiMi +MiA i+1 +AiM i +MiA i+1

Итак,

4 (A M2 + A M2 +...+ A M2 )= 2(A M2+ A M2 + ...+A M2)+ 2(A M2 +A M2 + ...+ A M2)= 1 1 2 2 n n 1 1 2 2 n n 2 1 3 2 1 n

= 2(A1M21 +M1A22+ ...+ AnM2n +MnA21)≥ A1A22+ A2A23+ ...+AnA21

По условию же имеется равенство, так что должно достигаться равенство в каждом из неравенств $2(AiM2i + MiA2i+1)≥ AiA2i+1,$ а это происходит при $AiM2i = MiAi+1.$

Таким образом, $Mi$ является серединой $AiAi+1$ для любого $i$ от $1$ до $n$ $(An+1 = A1).$ Поэтому точка $M$ является точкой пересечения серединных перпендикуляров к сторонам $A1A2 ...An,$ то есть центром описанной окружности. Далее пример для $n =6.$

$PIC$

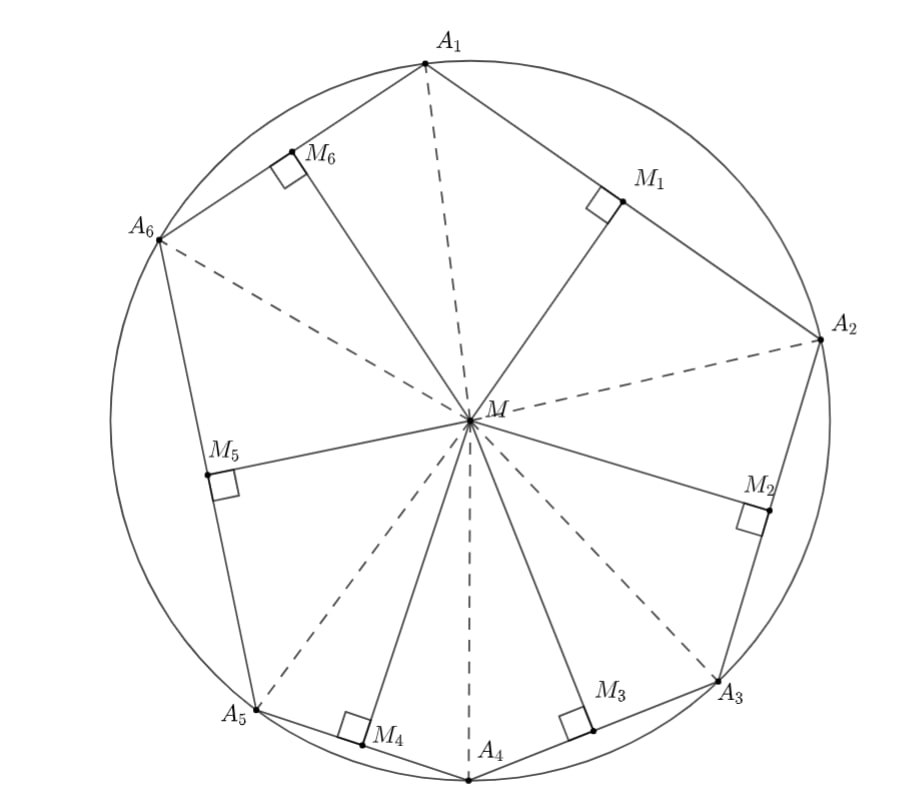
Ошибка.
Попробуйте повторить позже

Задача 6#128115

Решите уравнение $64(x2+ x)3 +1= 0.$

Источники: БИБН - 2025, 10.1 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Кажется, что разложить выражение на множители у нас не получится, тогда придется действовать иначе – перенести единицу в другую сторону и извлечь кубический корень из обеих частей уравнения!

Подсказка 2

Теперь мы получили обычное квадратное уравнение, которое легко можем решить, заметив формулу сокращённого умножения, либо же используя старый добрый дискриминант)

Показать ответ и решение

2 3 -1 (x + x) +64 = 0

( )3 (x2+ x)3 = − 1 4

Так как степень нечетная,

x2+ x= − 1 4

( 1)2 x+ 2 = 0

x= − 1 2

Ответ:

$− 1 2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#128116

Дана трапеция $ABCD$ с основаниями $AD = 2$ и $BC =1.$ Боковая сторона $AB,$ равная $1,$ перпендикулярна основаниям. На сторонах $BC$ и $CD$ взяты соответственно точки $M$ и $N$ такие, что $∘ ∠MAN = 45.$ Найдите все углы треугольника $MAN.$

Источники: БИБН - 2025, 10.2 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Нам дана очень хорошая трапеция, давайте найдём ее углы и попробуем понять что-то хорошее о четырёхугольнике АMCN.

Подсказка 2

Он вписанный! Так как сумма углов MCN и MAN равна 180º. Попробуем найти угол AMN, может на рисунке есть угол, равный ему?

Подсказка 3

Вписанные углы AMN и ACN опираются на одну и ту же дугу, а значит, они равны! А как найти угол ACN? Обратите внимание на равные отрезки, они помогут определить угол ВСА, а зная его, мы легко можем найти ACN, а значит, и все углы треугольника AMN)

Показать ответ и решение

$PIC$

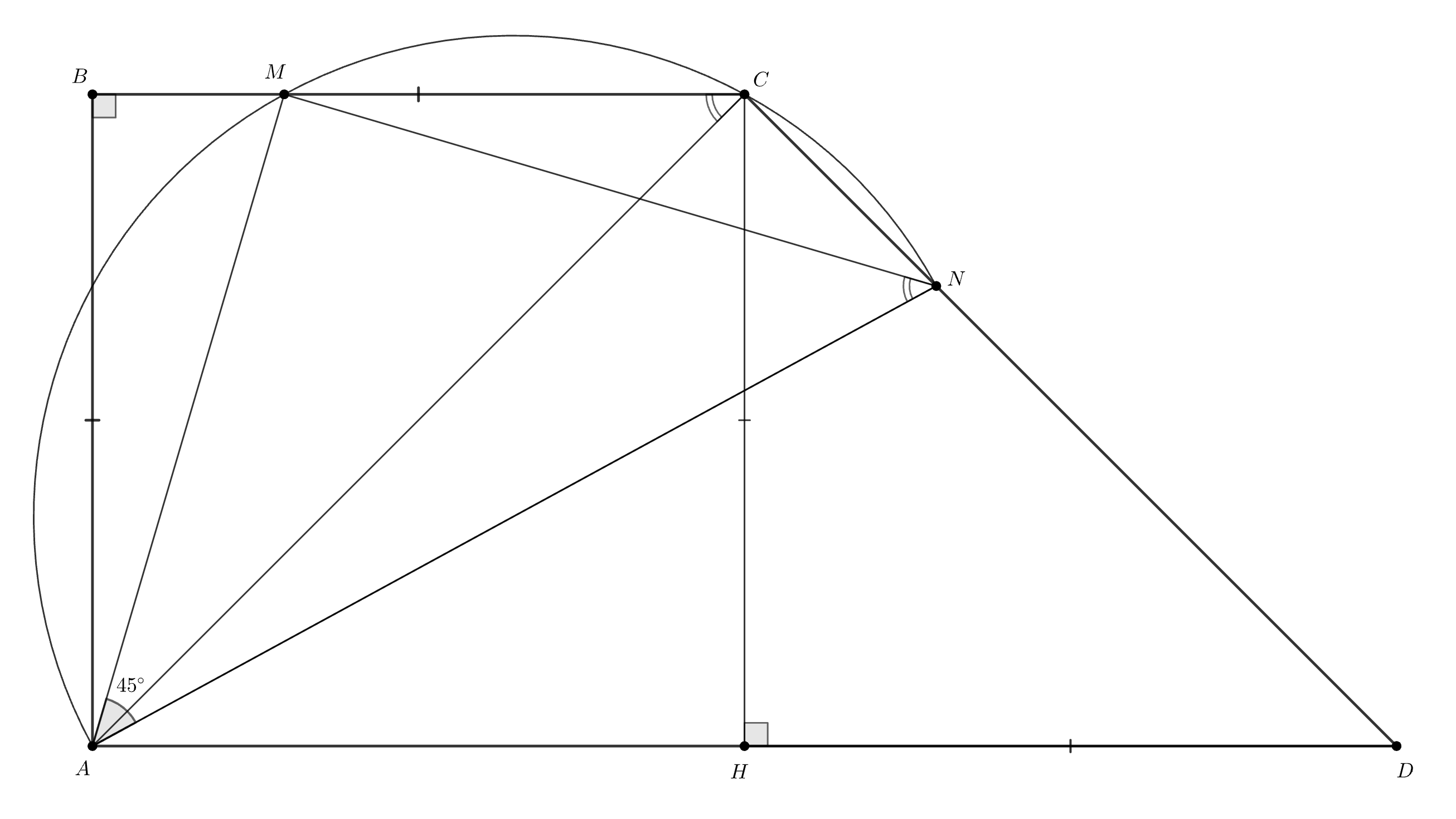
Поскольку $AB ⊥BC$ и $AB = BC,$ получаем, что $∠BCA = ∠BAC =45∘.$ Проведем высоту $CH.$ Она будет равна $AB =1,$ так как $AB ⊥ BC,$ $HD =AD − BC = 1= AB,$ тогда $∠CHD = 90∘,$ $∠HCD = ∠CDH =45∘.$ Кроме того, $AH = AD − HD = 1= HC,$ $∠ACH =∠CAH = 45∘.$ $∠ACD = 90∘,$ $∠BCD = 135∘.$ По условию, $∠MAN = 45∘,$ так как $∠MAN + ∠MCN =180∘,$ четырехугольник $AMCN$ является вписанным. $∠AMN =∠ACN = 90∘,$ $∠MNA = ∠MCA =45∘,$ как вписанные углы, опирающиеся на одну дугу.

Ответ:

$90∘,45∘,45∘$

Ошибка.
Попробуйте повторить позже

Задача 8#128117

Дан прямоугольный треугольник, у которого численные значения периметра и площади — числа рациональные. Обязательно ли а) длина гипотенузы — рациональное число? б) длина биссектрисы прямого угла — иррациональное число?

Источники: БИБН - 2025, 10.3 (см. www.unn.ru)

Подсказки к задаче

Пункт а, подсказка 1

Обозначим за а и b катеты нашего треугольника, за с – его гипотенузу. Чему равны площади и периметр? Можно ли как-то через них выразить с?

Пункт а, подсказка 2

Давайте вспомним, что стороны прямоугольного треугольника связаны с радиусом вписанной окружности, которую легко можно записать через периметр и площадь. Является ли радиус вписанной окружности рациональным числом? А что в этом случае можно сказать про гипотенузу?

Пункт b, подсказка 1

Нужно как-то связать площадь с биссектрисой, для этого разумно представить площадь как сумму площадей треугольников, на которые биссектриса делит △АВС, каждую из этих площадей легко можно записать через длину биссектрисы (обозначим ее за l) и катета! Что у нас получится?

Пункт b, подсказка 2

S = √2l(a + b)/4! Если мы поймём, к какому множеству чисел принадлежит сумма а + b, то сможем сделать вывод и о биссектрисе)

Пункт b, подсказка 3

a + b = P - c, помним, что Р и с – рациональные числа, а значит, сумма катетов тоже рациональна! Остается понять, какой должна быть длина биссектрисы, чтобы площадь была рациональной)

Показать ответ и решение

a) Пусть дан треугольник $ABC$ с $∠ACB = 90∘,$ $P$ — его периметр, $S$ — его площадь, $AC =b,$ $CB = a.$

$PIC$

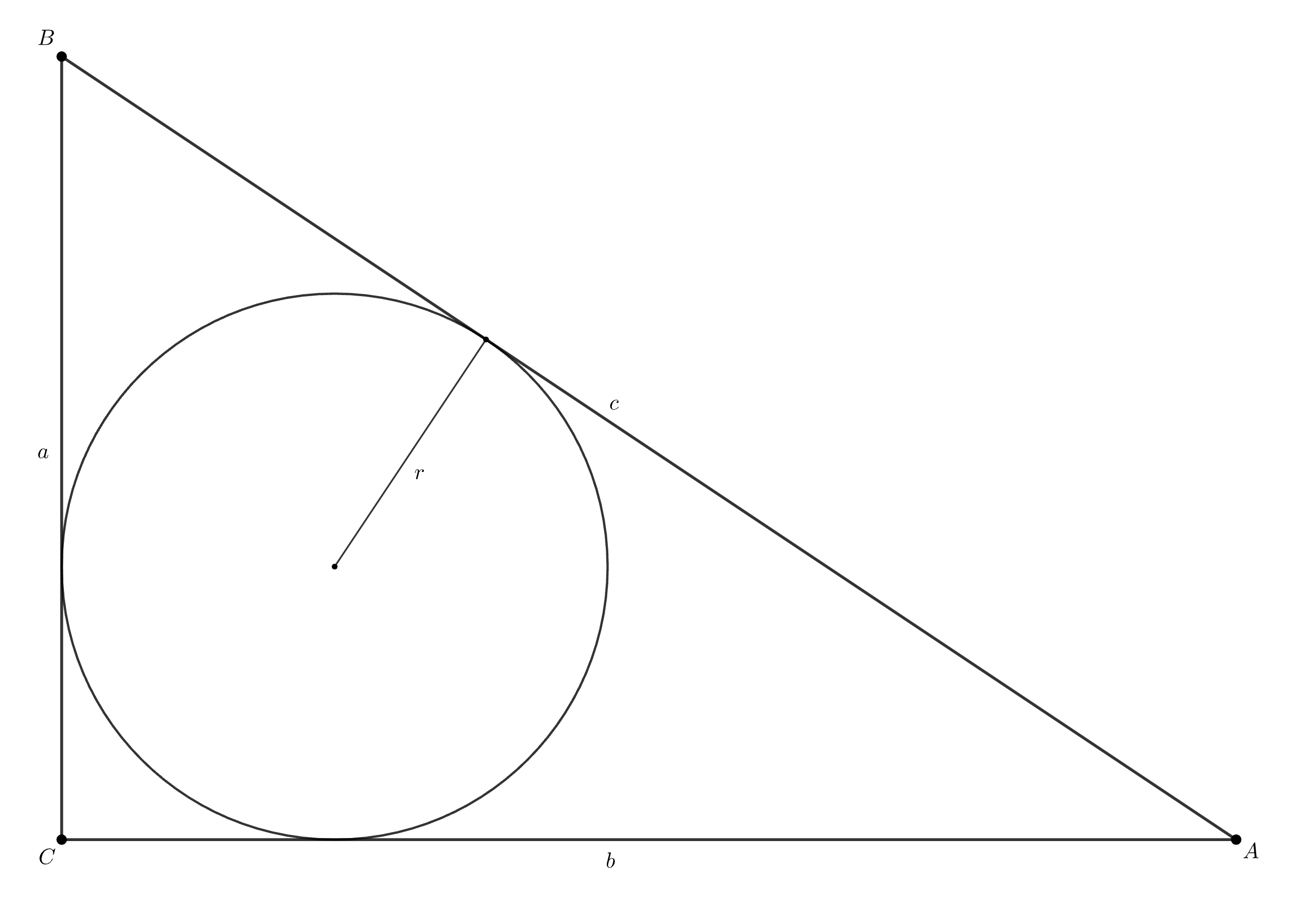
Тогда

1 S = 2ab

Пусть $r$ — радиус вписанной окружности, тогда

r= 2S P

С другой стороны, в прямоугольном треугольнике

r= a+-b−-c= P-− 2c 2 2

c= P-− r 2

Получаем, что $c$ — рациональное число.

б) Пусть $CD = l$ — биссектриса прямого угла.

$PIC$

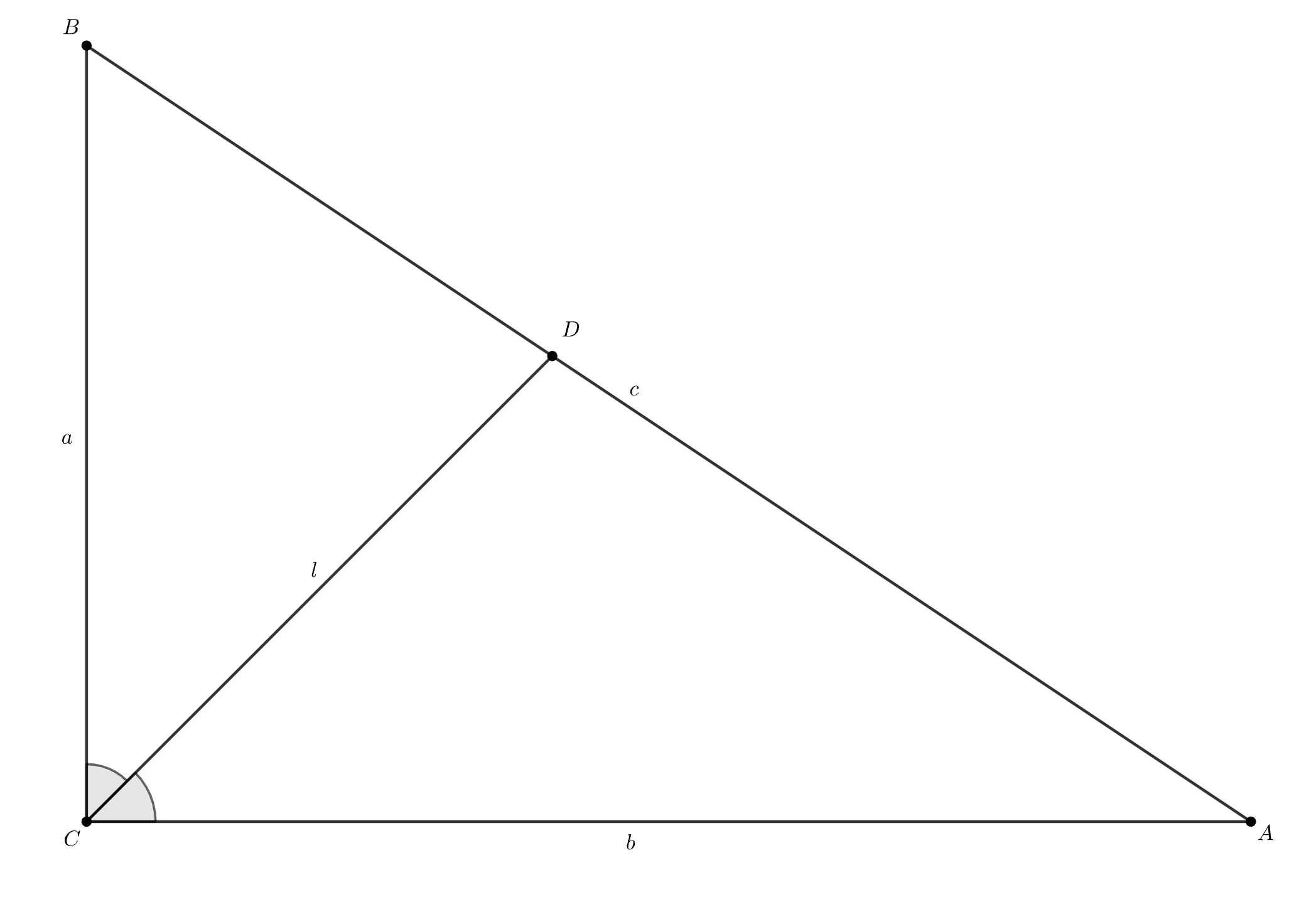
Из предыдущего пункта $a+ b= P − c$ — рациональное число. Так как $∘ ∠ACD =∠BCD = 45$

1 1 S = SACD +SBCD = 2 ⋅a ⋅l⋅sin(45∘)+ 2 ⋅b⋅l⋅sin(45∘)

√ - S = 1l(a+ b) 2 4

Если предположить, что $l$ — рациональное, то $S$ будет иррациональным, что противоречит условию. Значит, длина биссектрисы прямого угла — иррациональное число.

Ответ:

(a) обязательно; (b) обязательно

Ошибка.
Попробуйте повторить позже

Задача 9#128118

Сколько решений в целых числах $x,y$ имеет уравнение $6x2+2xy+ y+ x= 2025?$

Источники: БИБН - 2025, 10.4 (см. www.unn.ru)

Подсказки к задаче

Подсказка 1

Так как у входит в уравнение только в первой степени, давайте выразим у через х, что у нас получится? Как можно использовать тот факт, что х – целое число?

Подсказка 2

Выделим в полученной дроби целую часть и посмотрим на результат. В каких случаях полученное выражение будет целым?

Подсказка 3

Когда 2024/(2х + 1) – целое число! А сколько есть нечётных делителей у числа 2024 (не забудьте учесть отрицательные числа!)? Каждому такому делителю соответствует единственная пара чисел (х;у), так что количество нечётных делителей как раз и будет ответом к задачке)

Показать ответ и решение

Выразим $y:$

2025−-6x2− x y = 2x+1

Разделим $6x2+ x$ с остатком на $2x+ 1:$

6x2+ x= (3x− 1)(2x +1)+ 1

Тогда

2025− (3x− 1)(2x+ 1)− 1 2024 y =--------2x+-1------- = 2x-+1-− 3x+ 1

Тогда $y$ является целым тогда и только тогда, когда 2024 делится на нечетное число $2x +1.$ Знаем, что $2024= 8⋅11⋅23.$ Получаем, что $2x+ 1$ может принимать значения делителей $253= 11⋅23,$ а именно ${1;11;23;253}.$ Надо также учесть отрицательные числа, итого 8 значений.

Ответ:

$8$ решений

Ошибка.
Попробуйте повторить позже

Задача 10#128119

Докажите, что $20$ натуральных чисел: от $1$ до $20$ можно разбить на две группы так, чтобы сумма чисел первой группы равнялась произведению чисел второй. а) Какое наименьшее и б) какое наибольшее количество чисел может быть во второй группе?

Источники: БИБН - 2025, 10.5 (см. www.unn.ru)

Подсказки к задаче

Пункт а, Подсказка 1

Раз просят наименьшее, то давайте будем пробовать добавлять по одному числу, начиная с 0. Что будет, если у нас всего одно число во второй группе?

Пункт а, Подсказка 2

Сумма оставшихся чисел не меньше 190 — сильно много. Теперь для двух чисел во второй группе.

Пункт а, Подсказка 3

211 = (a+1)(b+1), бывает ли так?

Пункт а, Подсказка 4

211 — простое. Приведите пример для трёх чисел.

Пункт б, Подсказка 1

Как можно снизу оценить произведение через количество выбранных чисел?

Пункт б, Подсказка 2

Если чисел хотя бы 6, то произведение хотябы 6! = 720 > 210. Значит, чисел не больше 5.

Пункт б, Подсказка 3

Предположим, подойдёт пятёрка (1,2,3,4,x). Найдите x.

Показать ответ и решение

a) Сумма всех чисел от 1 до 20 равна 210. Очевидно, что во второй группе больше одного числа, так как в противном случае оно было бы равно сумме оставшихся 19 чисел, тоесть не меньше, чем $1+2 +...+ 19= 190.$ Покажем, что на самом деле во второй группе больше двух чисел. Действительно, в противном случае для чисел $a$ и $b$ из второй группы выполнялось бы равенство

210− a− b= ab

211= (a+1)(b +1)

Раз 211 — простое число, следовательно, данное уравнение не имеет решений на промежутке от 1 до 20. Приведем пример второй группы из 3 чисел. Сначала возьмем единицу, будет верно, что

209− a− b= ab

210= (a+1)(b +1)

Нам подойдут тройки ${1;9;20}$ и ${1;13;14}.$

б) Докажем, что чисел во второй группе меньше 6. В противном случае, наименьшее произведение чисел второй группы равнялось бы

1⋅2⋅3 ⋅4 ⋅5 ⋅6 =720> 210

Получили противоречие с равенством произведения чисел второй группы и суммы чисел первой группы. Подберем пример для случая, когда во второй группе 5 чисел. Предположим, что подойдет пятерка вида $(1;2;3;4;x),$ где $x ∈[5;20].$ Должно выполниться условие

210− 10− x= 24x

x= 8

Подойдет набор $(1;2;3;4;8).$

Ответ:

а) 3; б) 5