.02 Свойства функции
Ошибка.
Попробуйте повторить позже
Эту задачу можно решить как алгебраически, так и графически.
Первое решение.
(a) Докажем, что — возрастающая функция. Пусть
и
— произвольные значения аргумента, причём
Обозначим
через
и
соответствующие им значения функции:
Рассмотрим разность и
Разность положительна, так как
Аналогично,
положительна. Поэтому сумма
также положительна. Тогда
и
является возрастающей функцией, что и требовалось доказать.
(b) Докажем, что — убывающая функция. Пусть
и
— произвольные значения аргумента, причём
Обозначим
через
и
соответствующие им значения функции:
Рассмотрим разность и
Разность отрицательна, так как
А вот с разностью пока что не до конца понятно. Будем разбираться постепенно. Заметим, что
так как
Тогда
и разность
отрицательна.
и
отрицательны, поэтому их сумма также отрицательна. Тогда
и
является убывающей функцией,
что и требовалось доказать.
(c) Докажем, что — возрастающая функция. Пусть
и
— произвольные значения аргумента, причём
Обозначим
через
и
соответствующие им значения функции:
Рассмотрим разность и
Разность положительна, так как
Аналогично,
положительна.
А вот с суммой пока что не до конца понятно. Если
и
неотрицательные, то сумма будет неотрицательной, если
неположительные — то неположительной, если будут иметь разный знак, то сумма вообще может быть любой. Но! На самом деле, оба этих
числа будут неотрицательными, т. к. иначе их нельзя будет подставить в выражения
и
(число под знаком квадратного корня
всегда неотрицательно). Тогда сумма
неотрицательна.
положительна, а
— неотрицательна, поэтому их произведение тоже неотрицательно. Сумма неотрицательного числа и
положительного положительна. Тогда выражение
положительно. То есть
и
является
возрастающей функцией, что и требовалось доказать.
Второе решение.
Изобразим эскиз графика каждой из функций, составив таблицу значений.
Посчитаем некоторые значения функции от квадратов чисел, чтобы было удобно считать корень:
Таблица:
Изобразим полученные точки на графике:
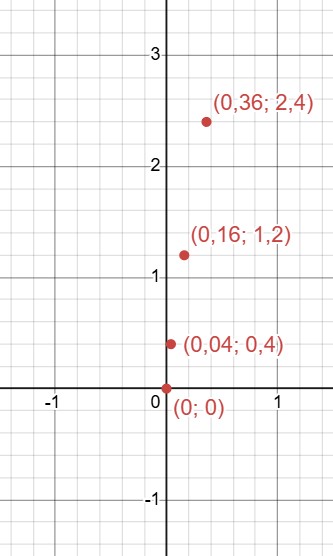
Соединим их:
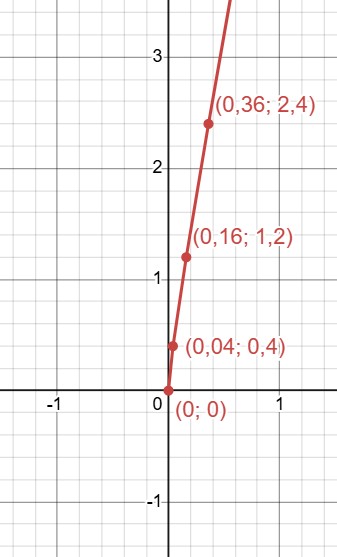
Видно, что функция возрастает.
Посчитаем некоторые значения функции от квадратов чисел, чтобы было удобно считать корень:
Начертим таблицу, округлив в ней значения до десятых, чтобы было удобно чертить график:
Изобразим полученные точки на графике:
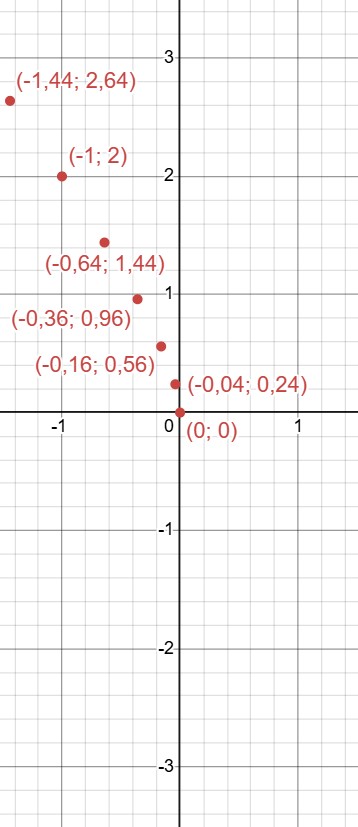
Соединим их:
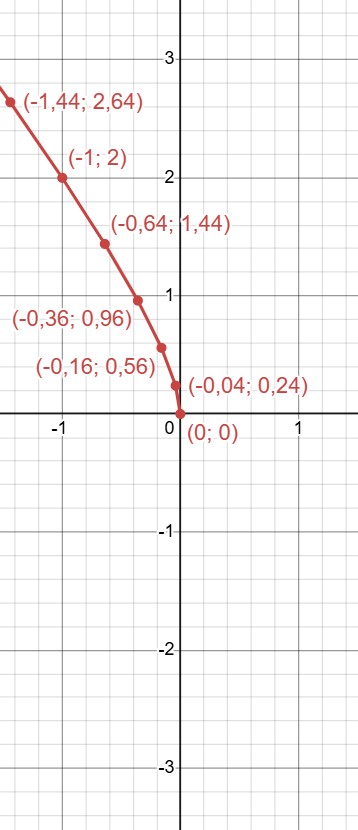
Видно, что функция убывает.
Посчитаем некоторые значения функции от квадратов чисел, чтобы было удобно считать корень:
Начертим таблицу, округлив в ней значения до десятых, чтобы было удобно чертить график:
Изобразим полученные точки на графике:
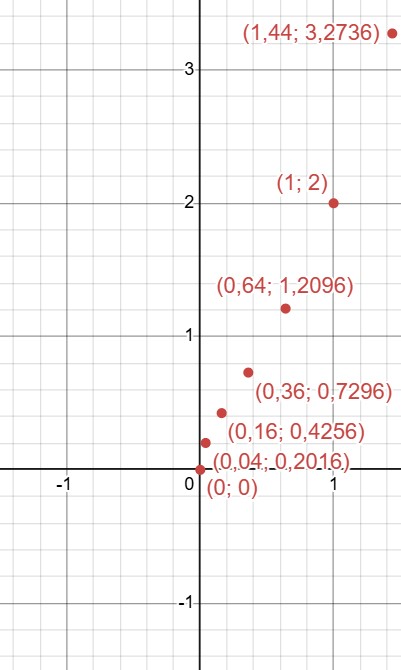
Соединим их:
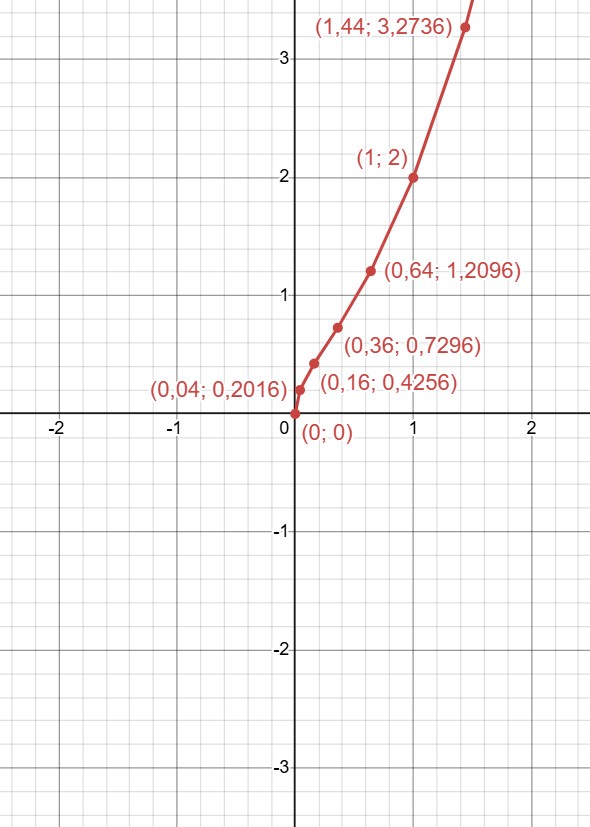
Видно, что функция возрастает.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




