Тема КФУ - задания по годам

КФУ 2025

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела кфу - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#103994Максимум баллов за задание: 7

Решите уравнение $arcsin(9x − 6)= arccos(7x− 5)$ .

Источники: КФУ - 2025, 11.1 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Изначально уравнение представлено в не самом приятном виде. Попробуем его преобразовать! Пусть t = arcsin(9x-6) = arccos(7x-5). Тогда удобно понимать, что t — некоторый угол. А что тогда можно сказать о синусе и косинусе этого угла?

Подсказка 2

Верно! Сумма квадратов синуса и косинуса t равна 1. Это необходимое условие того, чтобы уравнение имело решения! А какое условие будет достаточным?

Подсказка 3

Конечно! Не считая ОДЗ, достаточно, чтобы сумма квадратов 9x-6 и 7x-5 была равна 1. Теперь достаточно решить простенькое квадратное уравнение и найти ОДЗ!

Показать ответ и решение

Существует такой $x,$ при котором найдётся угол $α ∈ [0;π], α= arcsin(9x − 6)= arccos(7x− 5) 2$ тогда и только тогда, когда

( |{ 0≤ 9x− 6≤ 1 |( 0≤ 7x−25≤ 1 2 (9x − 6) + (7x− 5) =1

Уравнение из системы равносильно

2 2 81x − 108x+ 36+49x − 70x +25= 1

130x2− 178x+ 60= 0

x= 3 или x= 10 5 13

Но так как

9⋅ 3 − 6 = 27-− 6 <0, 5 5

то $x= 35$ не удовлетворяет первому неравенству системы.

А корень $x= 1103$ тривиальной подстановкой уже оказывается подходящим под неравенства системы.

Ответ:

$10 13$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#103995Максимум баллов за задание: 7

Пусть $a =√0,99...99$ (2024 девятки). Какова в этом числе:

а) 2024-ая;

б) 2025-ая

цифра после запятой?

Источники: КФУ - 2025, 11.2 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Мы знаем, что 0,9 = 1 - 10⁻¹, тогда наше подкоренное выражение можем записать как 1 - 10⁻²⁰²⁴. Хочется как-то ограничить a, попробуем ограничить через связь с (- 10⁻²⁰²⁴) = x, то есть, хотим получить f(x) < √(1+x) < g(x). Ведь в таком случае мы сможем что-то сказать о 2024-й и 2025-й цифре после запятой!

Подсказка 2

Так как значение под корнем меньше 1, то 1 + x < √(1+x) < 1, но нужна более точная оценка. Поможет, например, возведение в квадрат или деление.

Подсказка 3

Попробуем ограничить снизу 1+x/2 -x²/8, а сверху 1+ x/2, после доказательства сможем получить сразу и 2024-ую цифру, и 2025-ую!

Показать ответ и решение

$a =√1-− 10−2024.$ Обозначим $x= −10−2024.$ Докажем, что

x x2 √---- x 1+ 2 − 8 < 1 +x <1+ 2

Это неравенство из-за области значений $x$ эквивалентно возведённому в квадрат:

x2 x4 x2 x3 x2 1 +-4 + 64-+x − 4-− 8-< 1+ x< 1+x + 4-

Теперь правое неравенство очевидно в силу $2 0< x4-$ , а левое тоже в силу $4 3 x64 < x8 .$

Тогда получаем, что

−4048 1 − 5⋅10−2025− 10---< a< 1− 5⋅10− 2025 8

1− 6⋅10−2025 < a< 1− 5⋅10− 2025

a =0,9◟9..◝.◜99◞+4⋅10−2025+ 𝜀, 2024

где $−2025 𝜀 <10 .$

Ответ:

а) 9;

б) 4

Ошибка.
Попробуйте повторить позже

Задача 3#103996Максимум баллов за задание: 7

Любочка: “Вы сказали, что квадратное уравнение, заданное на дом, имеет не только целые ненулевые коэффициенты, но и два целых корня, а у меня получается, что корней вообще нет”.

Учитель: “Перед $2 x$ был написан коэффициент, а ты его пропустила, записывая задание в тетрадь”.

Можно ли утверждать, что Любочка может однозначно исправить свою описку на основе этой информации?

Источники: КФУ - 2025, 11.3 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Предположим, что верное задание имеет вид ax² + bx + c = 0. Можно ли подобрать b и c так, чтобы полученное уравнение имело целые корни более, чем при одном значении a?

Подсказка 2

Задействуем теорему Виета. Тогда b = -a(x₁ + x₂) и c = ax₁x₂. Что получится, если разделить одно уравнение на другое?

Подсказка 3

Верно! Теперь у нас стоит задача найти две пары целых x₁ и x₂, у которых суммы обратных величин совпадают и равны -b/c, а также уравнение x² + bx + c = 0 не имеет решений. А можно ли еще добыть информацию про a?

Подсказка 4

Представим ax² + bx + c = (x² + bx + c) + (1-a)x². Левая часть равна нулю, а в правой части первое слагаемое положительно, потому что не имеет нулей. Тогда второе слагаемое отрицательно, что возможно только при целом a < 0. А каков знак c?

Подсказка 5

Верно! c > 0, так как уравнение x² + bx + c = 0 не имеет корней. Тогда, поскольку c > 0 и a < 0, то корни x₁ и x₂ имеют разный знак. Имея такую, достаточно полную информацию, нужно придумать пример!

Показать ответ и решение

Любочка могла записать уравнение с целыми ненулевыми коэффициентами

2 x + 6x+ 36 =0,

которое не имеет корней, поскольку $x2+ 2⋅x⋅3+ 32 +27= (x+3)2+ 27 >0.$

При этом можно как дописать старший коэффициент -2:

2 − 2x + 6x+ 36= 0 ⇐ ⇒ x =− 3 или x =6,

так и дописать коэффициент -6:

− 6x2+ 6x+ 36= 0 ⇐ ⇒ x =3 или x= −2,

причём в обеих случаях получатся подходящие заданные учителем уравнения. Поэтому однозначно восстановить начальное уравнение Любочка уже не может.

_________________________________________________________________________________________________________________________________________________________________________________

Покажем, как можно составлять такие примеры, хотя это необязательно прописывать в решении на олимпиаде.

Пусть верное задание имело вид $ax2+ bx +c= 0$ . Попробуем подобрать $b$ и $c$ так, чтобы полученное уравнение имело целые корни более, чем при одном значении $a$ .

По теореме Виета $b= −a (x1+ x2);c= ax1x2$ . Исключим неизвестное $a$ из этой системы, поделив первое уравнение на второе. Это можно сделать, так как $c$ не равно 0 . Получаем равенство

b 1- 1- −c = x2 + x1.

Значит, надо подобрать две пары целых чисел ( $x1;x2$ ), для которых суммы обратных величин совпадают.

При этом надо учесть, что уравнение $2 x + bx +c= 0$ не имеет корней. Это значит, что все значения левой части положительны и, в частности, значение при $x= 0$ : $c >0$ .

Имеем

( ) ax2+bx+ c= x2 +bx+ c +(a− 1)x2.

При $x= x1$ или $x= x2$ эта сумма равна нулю, в то время как первое слагаемое положительно. Значит, $a< 1$ . В силу того, что $a$ целое, а уравнение — квадратное, $a< 0$ . Итак, с должно быть положительным, при этом $a$ — отрицательным. Из соотношения $c= ax1x2$ следует, что корни имеют разный знак.

Например,

12 + −13-= 13 + −16-= 16.

Подставляя пары корней $(2;−3)$ и $(3;−6)$ в теорему Виета, получим, что

b= −a1⋅(− 1)=− a2 ⋅(−3);c =a1⋅(−6)= a2 ⋅(−18).

Следовательно,

b=a1 = 3a2,c =−6b.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 4#103997Максимум баллов за задание: 7

Через каждую из сторон равностороннего треугольника $ABC$ со стороной 12 проведена плоскость, образующая угол $30∘$ с плоскостью этого треугольника. Эти три плоскости пересекаются в точке $D$ . Чему может быть равно расстояние от $D$ до плоскости треугольника?

Источники: КФУ - 2025, 11.4 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Интересно, где вообще может находиться точка D, в которой все три плоскости пересекаются? Если подумать о симметрии, куда она явно просится?

Подсказка 2

Окей, представим, что D висит прямо над центром треугольника. Теперь подумаем: если опустить из D перпендикуляр на плоскость АВС, получим точку О. А если из О и D провести перпендикуляры к стороне АВ, какой угол там получится? И как это связано с нашими 30°?

Подсказка 3

Хорошо, ОМ — это расстояние от центра до стороны. В равностороннем треугольнике оно легко считается. Но тут есть нюанс: а если О — это не центр вписанной окружности, а центр вневписанной? Как тогда изменится ОМ, и что это даст для h? Попробуйте рассмотреть оба варианта!

Показать ответ и решение

Опустим из точки $D$ перпендикуляр на плоскость $ABC,$ назовем полученную точку $O.$ Проведем из точек $D$ и $O$ перпендикуляры к $AB,$ по теореме о трех перпендикулярах получим одну и ту же точку $M.$

Обозначим длину искомого отрезка $DO$ за $h.$ Тогда катет $OM$ полученного прямоугольного треугольника $DOM$ с углом $∘ ∠DMO = 30$ равен $√- 3h.$

В силу симметрии треугольника $ABC$ точка $O$ равноудалена от прямых $AB,$ $BC$ и $AC$ на расстояние $√ - 3h,$ значит, $O$ либо центр вписанной окружности, либо центр одной из вневписанных окружностей треугольника $ABC.$

Найдем расстояние между стороной $AB$ и центром вписанной окружности $O :$

$PIC$

Так как $ABC$ — равносторонний, то высота $OM$ является медианой, значит, $MB = 6.$ Следовательно, $OM = 6⋅tg30∘ = 2√3,$ тогда $√3h = 2√3,$ откуда $h =2.$

Рассмотрим случай, когда точка $O$ оказалась центром вневписанной окружности:

$PIC$

Тогда получим равносторонний треугольник $ABO$ со стороной $AB = 12.$ Найдем длину высоты $√ - OM = 12⋅cos60∘ = 6 3,$ значит, $√ - √ - 3h = 6 3,$ откуда $h =6.$

Ответ: 2 или 6

Ошибка.
Попробуйте повторить позже

Задача 5#103998Максимум баллов за задание: 7

При каких значениях параметра $a$ три различных параболы с уравнениями $y = ax2+ x+ 1; y = x2+ax+ 1; y = x2+ x+ a$ имеют общую касательную? (Точки касания не обязаны совпадать)

Источники: КФУ - 2025, 11.5 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Пусть y = kx + b — касательная. Касание каждой параболы дает 3 уравнения на равенство функций, причем каждое уравнение имеет единственное решение. Какая система тогда получится?

Подсказка 2

У нас есть три уравнения ax² + x + 1 = kx + b, x² + ax + 1 = kx + b, x² + x + a = kx + b. Каждое из них из-за касания имеет единственное решение. Какие три условия тогда можно еще записать?

Подсказка 3

Верно! Условия на равенство дискриминантов нулю. Тогда выходит, что (1-k)² = 4a(1-b), (a-k)² = 4(1-b), (1-k)² = 4(a-b). Как решать такую систему?

Подсказка 4

Точно! Из первого и третьего уравнений легко получить, что b = 0 при любых a или a = 1 при любых b. Какой из двух случаев реализуется?

Подсказка 5

Конечно, a = 1 не подходит, так как тогда две из трех парабол в условии совпадают. Тогда b = 0. Что получится, если это подставить?

Показать ответ и решение

Пусть $y =kx+ b$ — касательная из условия. Выразим условия пересечения прямой $y$ с каждой из парабол:

2 2 2 ax + x+ 1= kx+b, x +ax+ 1= kx+ b, x +x +a= kx+ b

Так как прямая является касательной к каждой из них, значит, у каждого уравнения должно быть единственное решение, получаем систему, приравнивая дискриминант каждого уравнения к нулю:

(| (1− k)2 − 4a(1− b)= 0 { (a− k)2− 4(1− b)= 0 |( (1− k)2 − 4(a− b)= 0

(|{ (1− k)2 = 4a(1− b) (a− k)2 = 4(1− b) |( (1− k)2 = 4(a− b)

Из первого и третьего уравнений:

4a(1− b)= 4(a− b)⇒ a − ab= a− b⇒ ab= b

Отсюда возможно два случая:

[ b =0, для лю бого a a =1, для любого b

Значение $a= 1$ не подходит, так как тогда первая и третья параболы совпадают, что противоречит условию об их различии.

Так как $b= 0,$ верно:

{ (1− k)2 = 4a (a− k)2 = 4

{ (1− k)2 = 4a k =a∓ 2

Получаем 2 случая:

[ (3− a)2 = 4a, если k= a− 2 (1+ a)2 = 4a, если k= a+ 2

Решения: $a= 1$ при $k= 3,$ $a= 1$ при $k =− 1,$ $a= 9$ при $k =7.$

Из всех решений подходит только одно: $a= 9$ при $k= 7.$ Получаем единственное значение параметра: $a= 9.$

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 6#129307Максимум баллов за задание: 7

В корзине лежат яблоки и мандарины, причем яблоки составляют менее $92%$ всех фруктов. Любочка добавляет в корзину фрукты по одному, так что в какой-то момент доля яблок становится больше $92%.$ Обязательно ли был момент, когда доля яблок была в точности равна $92%?$

Источники: КФУ - 2025, 10.1 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

От чего по сути зависит доля яблок? Логичным будет ввести соответствующие переменные и записать условие задачи в виде парочки неравенств. Есть ли у такой системы целые решения?

Подсказка 2

Запишем неравенствами: знаменатель, составляющий количество фруктов, тут явно положительный, поэтому можем смело всё на него всё умножить! Что остаётся в итоге? Попробуйте зажать какую-то величину между двумя другими.

Подсказка 3

С учётом того, что все количества целые, мы получаем однозначную связь между количеством яблок и общим числом фруктов в корзине. Осталось лишь подобрать целое решения для уравнения с двумя переменными, и задача решена!

Показать ответ и решение

Запишем проценты в виде обыкновенной дроби, $92% = 23. 25$ Пусть в некоторый момент в корзине лежит $n$ фруктов, причем доля яблок меньше, чем $23 25,$ а после добавления одного фрукта их стало больше, чем $23- 25.$ Ясно, что в этот момент добавили яблоко (пусть их было $k,$ тогда стало $k +1).$ Имеем

k 23 k+1 23 n < 25, n-+1 > 25

{ 25k <23n 25k +25> 23n+ 23

Соотношения принимают вид:

23n− 2< 25k <23n

25k= 23n− 1

Осталось подобрать $n$ так, чтобы $23n− 1$ делилось на $25.$ Перебором получаем, что подходит $n =12,$ $k= 11.$

Проверим: Пусть в какой-то момент в корзине 11 яблок и 1 мандарин, доля яблок $1112-≈ 0,917 <92%.$ Добавим 1 яблоко, получим 12 яблок из 13 фруктов, доля равна $12-≈ 0,923 >92%. 13$

Заметим, что подходящее $n$ не обязательно искать перебором. Имеем соотношение

23n− 25k= 1

23(n− k)= 2k +1

Значит, $2k +1$ — нечетное число, делящееся на $23.$ Например, возьмём $2k +1 =23,$ тогда $k = 11,$ $n − k= 1,$ т.е. $n= 12.$ Это минимальное решение.

Ответ:

Нет

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#129309Максимум баллов за задание: 7

Дан ребус КАР + КАР $+...+$ КАР $=$ РРРРР (одинаковым буквам соответствуют одинаковые цифры, разным — разные). При каком наименьшем числе слагаемых он имеет решение?

Источники: КФУ - 2025, 10.2 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Когда много-много раз складывают одни и те же числа, на что это похоже? Тогда какими свойствами числа РРРРР стоит поинтересоваться?

Подсказка 2

Конечно же, нас интересует делимость! На что точно делится число, состоящее из пяти одинаковых цифр? Попробуйте представить правую часть уравнения в виде произведения Р и нескольких простых множителей.

Подсказка 3

Осталось лишь немного порассуждать: на какой из этих множителей может делиться КАР и сколько будет слагаемых в каждом из случаев!

Показать ответ и решение

Имеем

РРРРР =Р ⋅11111= Р⋅41⋅271= n⋅КАР

Если КАР не делится на простое число 271, то на него делится $n,$ так что в этом случае оно не меньше, чем 271.

Пусть теперь $КАР = 271k.$ Ясно, что число $k$ не превосходит 3, так что оно взаимно просто с 41. Значит, на 41 делится число $n.$

При 41 слагаемом ребус будет иметь три решения, для $k$ от 1 до 3. А именно,

271+ 271+ ⋅⋅⋅+ 271 =271⋅41= 11111

Аналогично

542+ 542+ ⋅⋅⋅+ 542 =542⋅41= 22222

А так же

813+ 813+ ⋅⋅⋅+ 813 =813⋅41= 33333

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 8#129311Максимум баллов за задание: 7

Вовочке задали на дом квадратное уравнение. «Учитель сказал, что оно имеет два целых корня, а у меня получается, что корней нет» — пожаловался он. Его папа-математик, посмотрев на уравнение, сказал: «Ты, наверное, неправильно списал с доски один из коэффициентов. Если это так, то я знаю правильный вариант задания, причем он единственный».

Докажите, что, если папа прав, то свободный член уравнения Вовочка записал верно.

Источники: КФУ - 2025, 10.3 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Запишите квадратное уравнение в общем виде. Как можно переформулировать условие задачи?

Подсказка 2

Пусть Вовочка записал уравнение ax² + bx + c = 0. Попробуйте пойти от противного.

Подсказка 3

Предположим, что уравнение ax² + bx + c = 0 не имеет решений, и существует единственное c₁, такое, что ax² + bx + c₁ = 0 имеет 2 решения. Тогда мы должны прийти к противоречию, поскольку если папа прав, то Вовочка записал свободный член верно.

Подсказка 4

Воспользуйтесь теоремой Виета.

Подсказка 5

Докажите, что c₁ — не единственный свободный коэффициент, при замене на который уравнение будет иметь 2 решения.

Подсказка 6

Также надо доказать, что ситуация, описанная папой, возможна. Для этого достаточно привести пример.

Показать доказательство

Пусть Вовочка записал уравнение в виде

2 ax +bx+ c= 0

и оно не имеет корней. Предположим, что можно заменить свободный член так, чтобы у уравнения появились два целых корня. Пусть верное задание имеет вид

ax2+ bx +c = 0 1

корни его обозначим $x1,x2.$ По теореме Виета

b=− a(x1+ x2), c1 = ax1x2

То есть $n= x1+x2 =− ba$ — целое число. Сохраняя эту сумму, можно менять корни и, соответственно, их произведение. То есть в качестве $c1$ можно рассмотреть числа 0, $a⋅1⋅(n− 1),$ $a ⋅2 ⋅(n− 2)$ и т.д. Итак, в этом случае исправление не единственное.

Например, пусть Вовочка решал уравнение

1x2+ x+ 1=0 2

Здесь $n =− 2.$ Значит, «восстановленное» уравнение может иметь вид

1x2+x +0 =0, 2

1x2 +x− 3 =0, 2 2

1 2 2x + x− 4=0

Папа не смог бы сказать, которое из них было задано на дом.

Мы показали следующий факт: если можно исправить уравнение за счёт свободного члена, то это исправление не единственное. Вообще говоря, надо ещё показать, что ситуация, описанная папой, возможна. Например, рассмотрим уравнение

3x2+x +2 =0

Если не менять первый коэффициент, то новое уравнение имеет вид

2 3x + b1x+c1 = 0,

где либо $b1 = 1,$ либо $c1 = 2.$ Но тогда числа $b13-=− (x1+ x2)$ и $c13-=x1x2$ не могут быть оба целыми. Значит, уравнение нельзя исправить за счет второго или третьего коэффициента, так как ни один из них не делится на 3. Попробуем найти «правильный» коэффициент $a.$ Ясно, что он должен быть делителем как 1, так и 2, то есть подходят только $a =1$ и $a =− 1.$

Уравнение

2 x + x+ 2= 0

не имеет решений, а уравнение

−x2+ x+ 2=0

имеет целые корни $x =− 1$ и $x =2.$ Именно оно и будет единственным возможным исправлением исходного уравнения.

Замечание. Без условия целочисленности корней утверждение задачи также будет верным. Однако без этого ограничения неверным будет высказывание папы, так что из него может следовать что угодно.

Ошибка.
Попробуйте повторить позже

Задача 9#129312Максимум баллов за задание: 7

Задан выпуклый четырехугольник, в нем проведены биссектрисы всех четырех углов. Может ли оказаться, что каждую из сторон (в ее внутренней точке) пересекает хотя бы одна из биссектрис?

Источники: КФУ - 2025, 10.4 (см. malun.kpfu.ru)

Подсказки к задаче

Подсказка 1

Как биссектрисы должны пересекать стороны?

Подсказка 2

Каждую сторону должна пересечь ровно одна биссектриса. Как могут взаимно располагаться биссектрисы?

Подсказка 3

Например, если в четырёхугольнике ABCD биссектриса ∠A пересекает сторону BC, то биссектриса ∠D должна пересекать сторону AB.

Подсказка 4

А что нам вообще могут дать биссектрисы? Какие у них есть свойства?

Подсказка 5

Рассмотрите диагонали четырёхугольника.

Подсказка 6

Посмотрите, как биссектрисы делят диагонали. Для этого надо воспользоваться свойством биссектрисы об отношении сторон и отрезков в треугольнике.

Показать ответ и решение

Если каждую сторону во внутренней точке пересекает какая-то биссектриса, то каждую из них пересекает ровно одна.

Пусть для определенности биссектриса угла $A$ пересекает сторону $BC$ (длиной $a$ ). Биссектриса угла $D,$ вообще говоря, может пересекать $AB$ или $BC,$ но в силу условия пересекает сторону $AB$ (длиной $d).$ Аналогично получаем, что биссектриса угла $C$ пересекает сторону $DA$ (длиной $c)$ и биссектриса угла $B$ — сторону $CD$ (длиной $b).$

Пусть биссектриса угла $A$ пересекает диагональ $BD$ в точке $P,$ а биссектриса угла $C$ в точке $Q.$

$PIC$

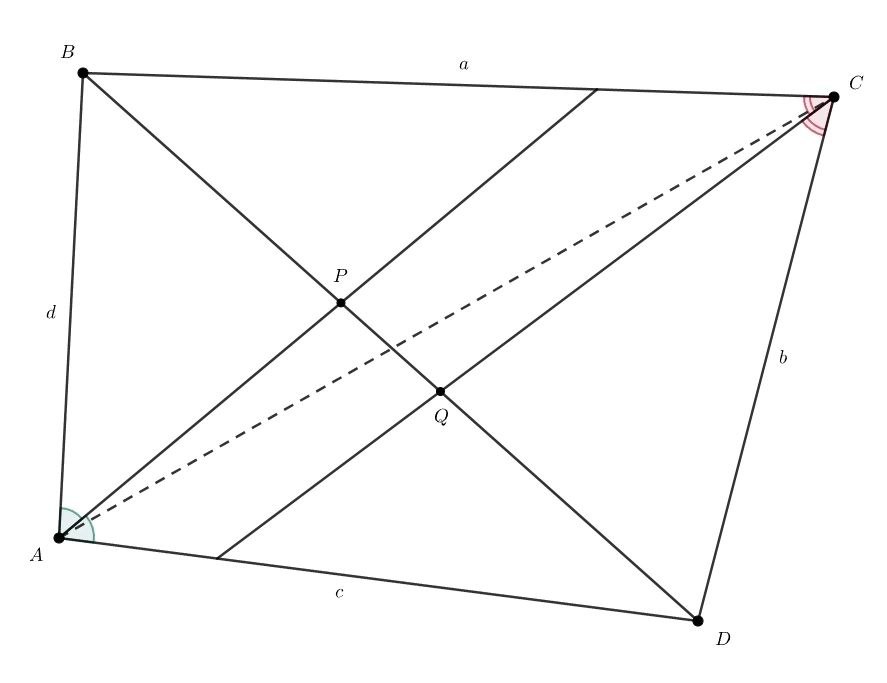
Заметим, что по свойству биссектрисы

BP-= d и BQ- = a PD c QD b

Но биссектриса угла $A$ пересекает диагональ $BD$ ближе к вершине $B,$ чем биссектриса угла $C.$ Значит,

d a c < b

bd< ac

Аналогичное исследование второй диагонали показывает, что

c < d b a

bd> ac

Пришли к противоречию.

Ответ:

Нет, не может

Ошибка.
Попробуйте повторить позже

Задача 10#129314Максимум баллов за задание: 7

На ферме по выращиванию жемчуга проводится акция: посетителю разрешают вскрыть несколько раковин, до тех пор, пока он не найдет 2 жемчужины. В каждой раковине может быть не более одной жемчужины, причем вероятность, что она там будет, равна $1∕3.$ Аделаида Ивановна участвует в акции. Какова вероятность того, что она вскроет: а) ровно 4 раковины; б) не менее 4 раковин?

Источники: КФУ - 2025, 10.5 (см. malun.kpfu.ru)

Подсказки к задаче

Пункт а, Подсказка 1

Давайте порассуждаем: в каком случае вскрыто ровно 4 раковины? В какой из раковин жемчужина при этом точно была, а в какой – не факт? Сколько у нас подходящих вариантов?

Пункт а, Подсказка 2

Каждая раковина – независима от другой. Что в таком случае надо делать с вероятностями?

Пункт а, Подсказка 3

Итак, вероятности перемножили, осталось лишь понять, сколько у нас подходящих равновероятных комбинаций и произвести соответствующие действия!

Пункт б, Подсказка 1

Как будто бы напрямую тут слишком много случаев рассматривать, попробуем тогда пойти от противоположного события! Какое событие противоположно к искомому?

Пункт б, Подсказка 2

По сути нам надо из 1 вычесть сумму вероятностей того, что вскрыто ровно 2 или ровно 3 раковины. Осталось лишь решить задачу, аналогичную пункту а) и внимательно всё вычислить!

Показать ответ и решение

а) Ясно, что А.И. найдёт жемчужину в 4-ой раковине, а также ровно в одной из предыдущих. Имеем три варианта события, вероятность каждого равна