.01 Графический метод решения
Ошибка.
Попробуйте повторить позже
и 
при которых система уравнений
График уравнения 
— прямая, проходящая через точки 
и 
(a) Мы хотим, чтобы система имела бесконечно много решений,значит, прямые 
и 
должны совпадать. Тогда
мы должны подобрать такой коэффициент 
при котором 
и 
могут совпадать или быть параллельны друг другу,
а потом подобрать такой коэффициент 
чтобы прямые совпали.
Начнём с поиска 
Прямая 
параллельна 
Тогда, если мы найдём 
при котором прямая
параллельна 
то это значение 
подойдёт в качестве ответа. График 
— множество прямых,
проходящих через 
Будем вращать линейку около этой точки, пока прямые 
и 
не будут
параллельны:
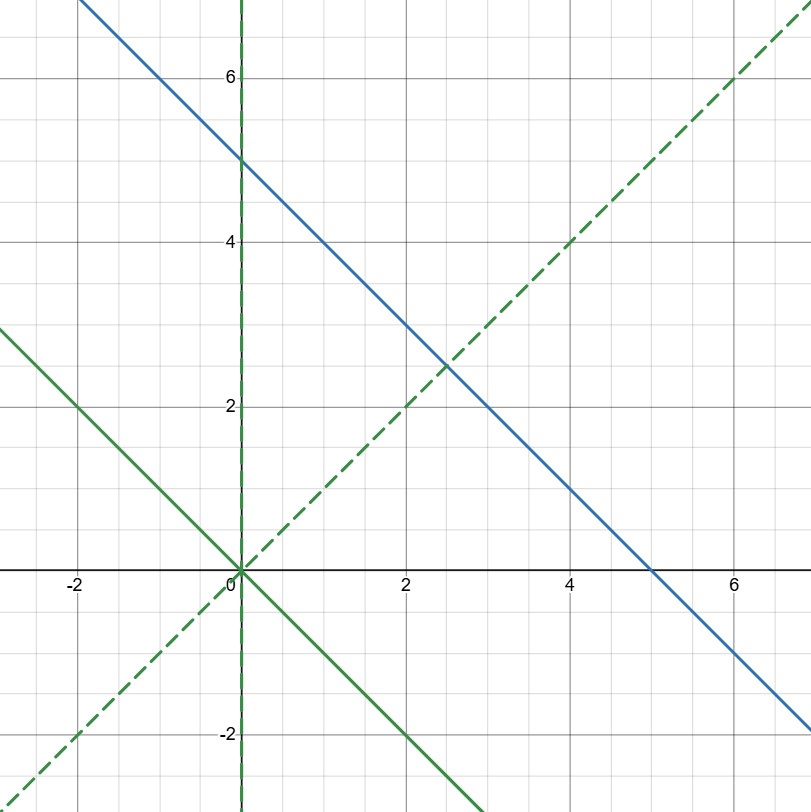
Таким образом, 
Вернёмся к прямой 
которая, как мы выяснили, на самом деле является прямой 
Это множество прямых,
параллельных прямой 
Чтобы выяснить, при каком значении 
система уравнений имеет бесконечно много решений, нам надо
перемещать линейку параллельно этой прямой, пока прямые 
и 
не совпадут, а потом найти значение параметра
Таким образом, 
(b) Мы хотим, чтобы система не имела решений, значит, прямые 
и 
должны быть параллельны. Как мы
выяснили в предыдущем пункте, эти прямые могут быть параллельны только при 
При этом 
иначе они будут совпадать.
Система не будет иметь решений при 
и 
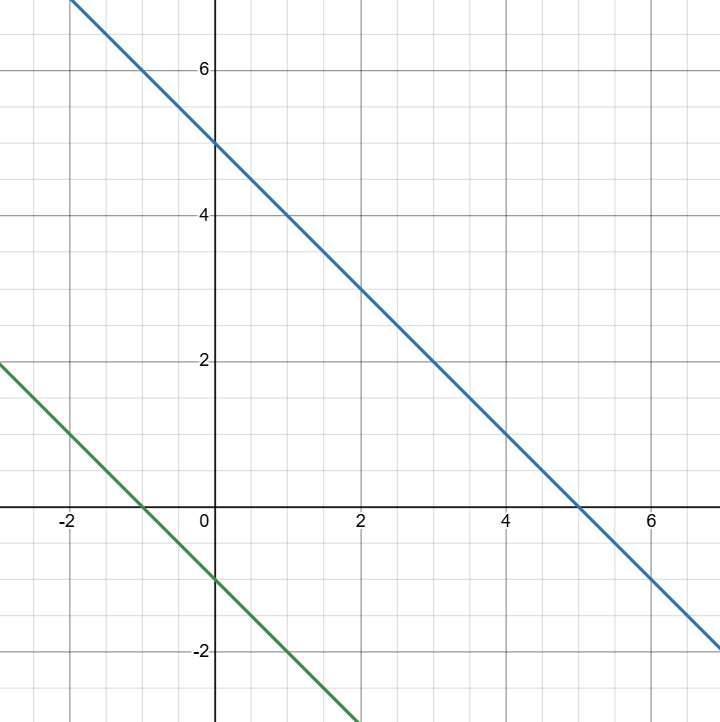
В ответ можем записать, к примеру, пару чисел 
и 
(c) Система будет иметь единственное решение, если прямые 
и 
не будут совпадать и не будут параллельны,
т. е. будут пересекаться. Поскольку они совпадают или параллельны только при 
нам подходит любое 
и любое
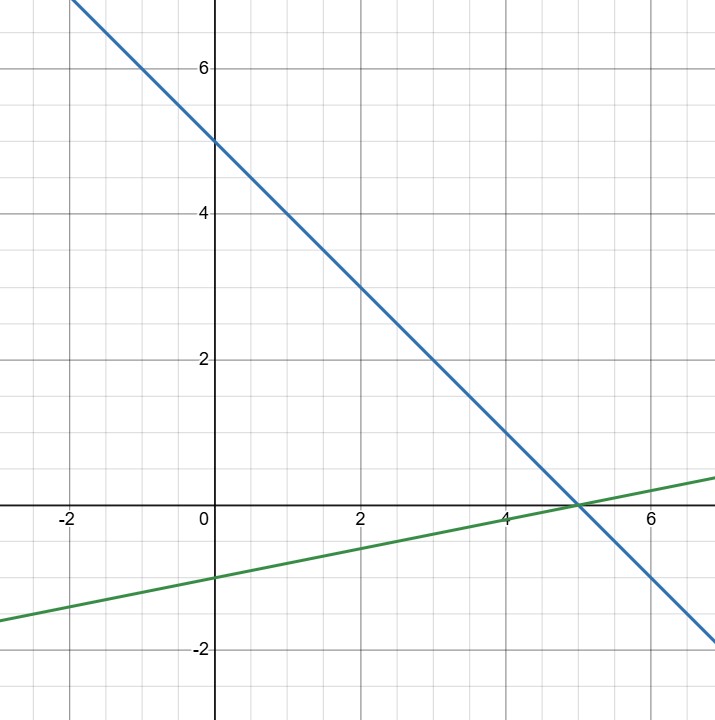
В ответ можем записать, к примеру, пару чисел 
и 
и любое 
например, 
и любое 
например, 
и
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
