ЮМШ 2020
Ошибка.
Попробуйте повторить позже
Две окружности, вписанные в угол с вершиной 
, пересекаются в точках 
и 
. Через 
проведена прямая, пересекающая меньшую
окружность в точке 
, а большую — в точке 
. Оказалось, что 
.
1. Пусть 
и 
совпали с точками касания окружностей и угла. Докажите, что угол 
прямой.
2. Пусть 
и 
совпали с точками касания окружностей и угла. Чему может быть равен угол 
?
3. Докажите, что если 
прямой, то 
и 
совпадают с точками касания окружностей и угла.
4. Какие значения может принимать угол 
, где 
— центр меньшей окружности?
Источники:
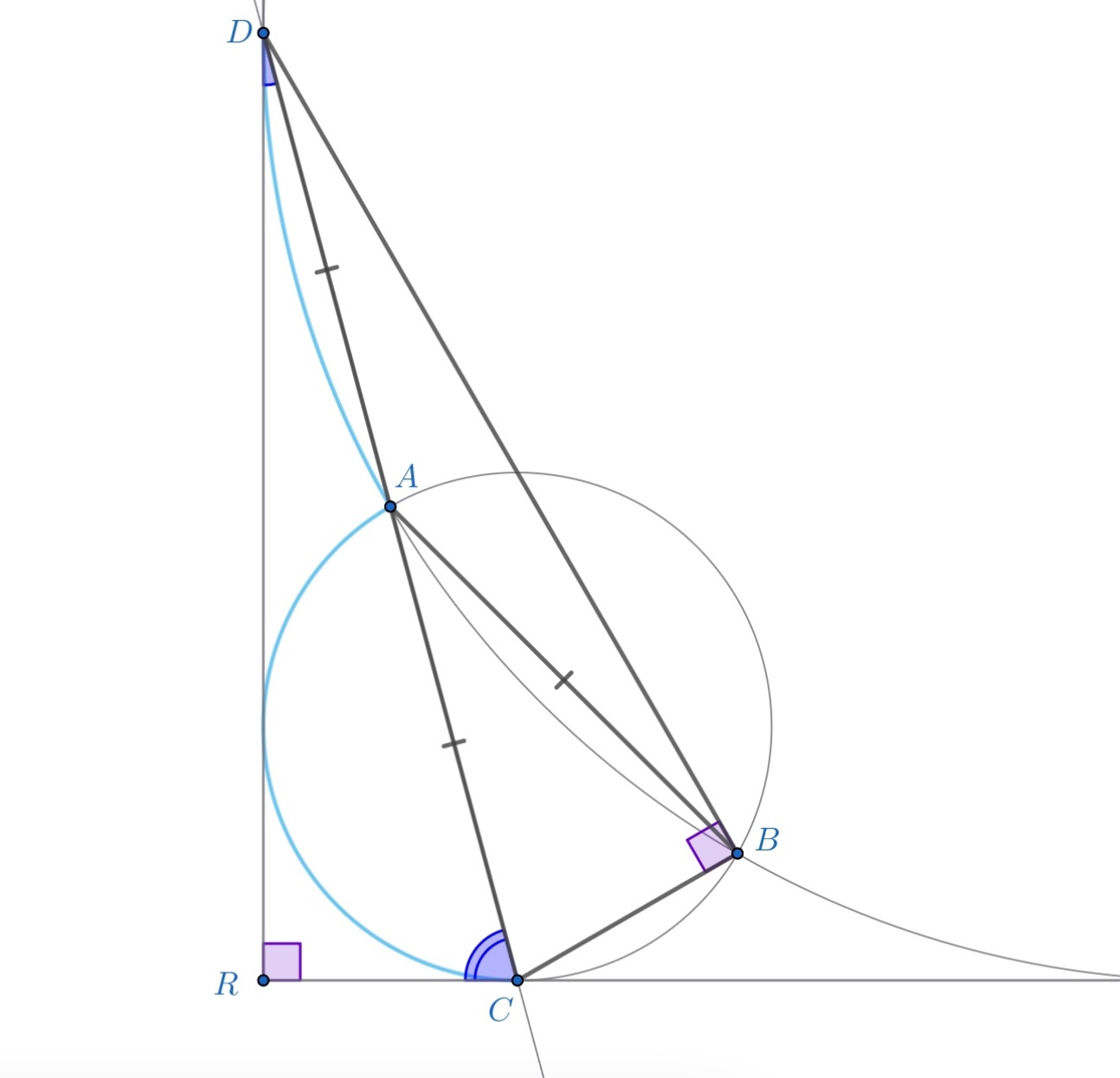
1. Треугольник 
прямоугольный (медиана — половина гипотенузы). Значит, сумма дуг 
и 
соответствующих
окружностей равна 
, а сумма соответствующих углов между хордой и касательной 
, поэтому
.
_________________________________________________________________________________________________________________________________________________________________________________
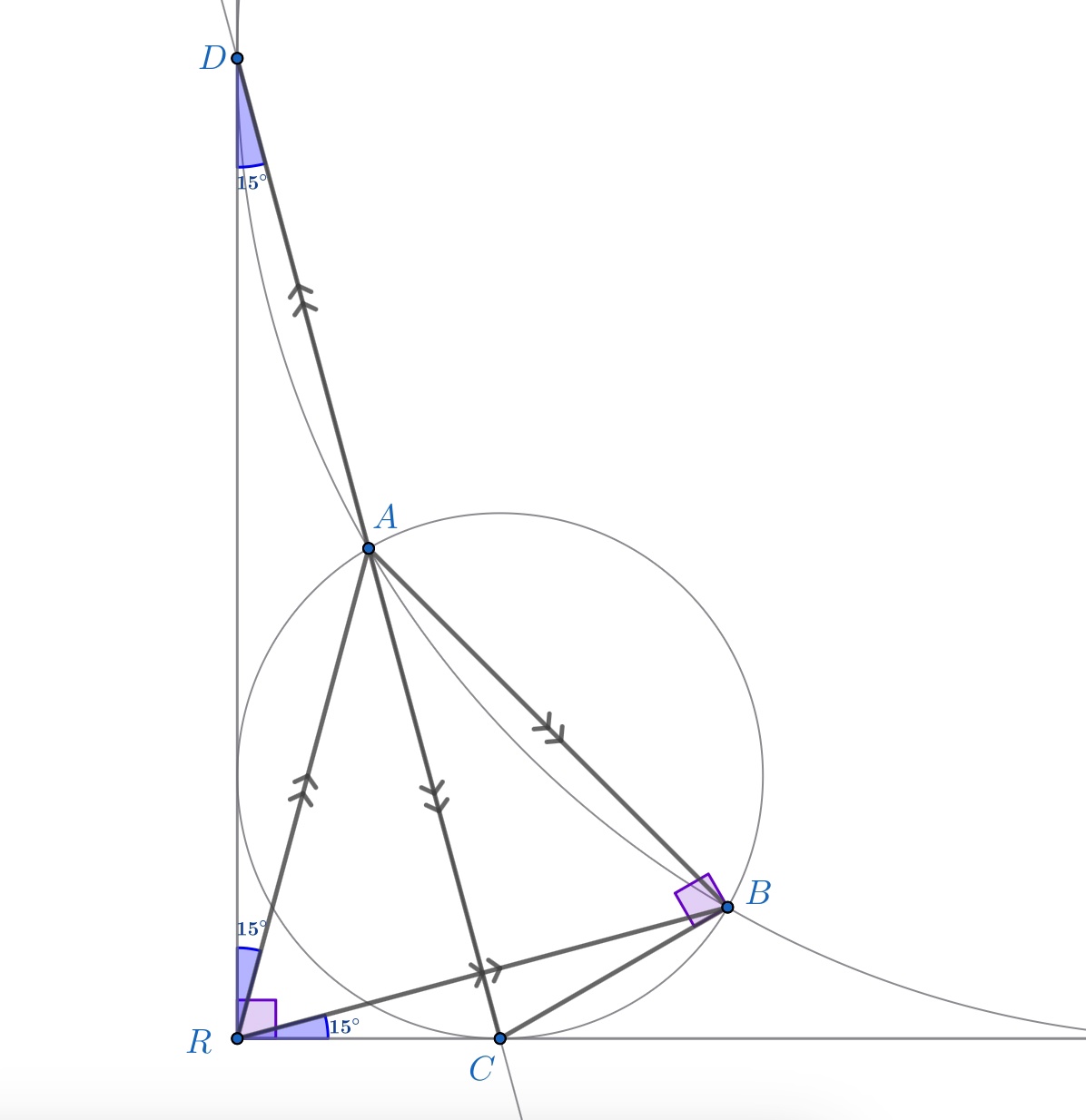
2. Треугольник 
равносторонний 
и 
по симметрии. Отсюда симметричные отрезки 
образуют со сторонами углы, равные 
и этому же равен 
(т.к. 
).
_________________________________________________________________________________________________________________________________________________________________________________
3. Выполним инверсию 
относительно окружности с центром в 
и радиусом 
. Имеем 
, и наши две
окружности превращаются в прямые 
, образующие прямой угол, а стороны исходного угла - в пару окружностей, вписанных в этот
угол, перпендикулярных друг другу (как и соответствующие прямые до инверсии) и пересекающихся в точках 
.
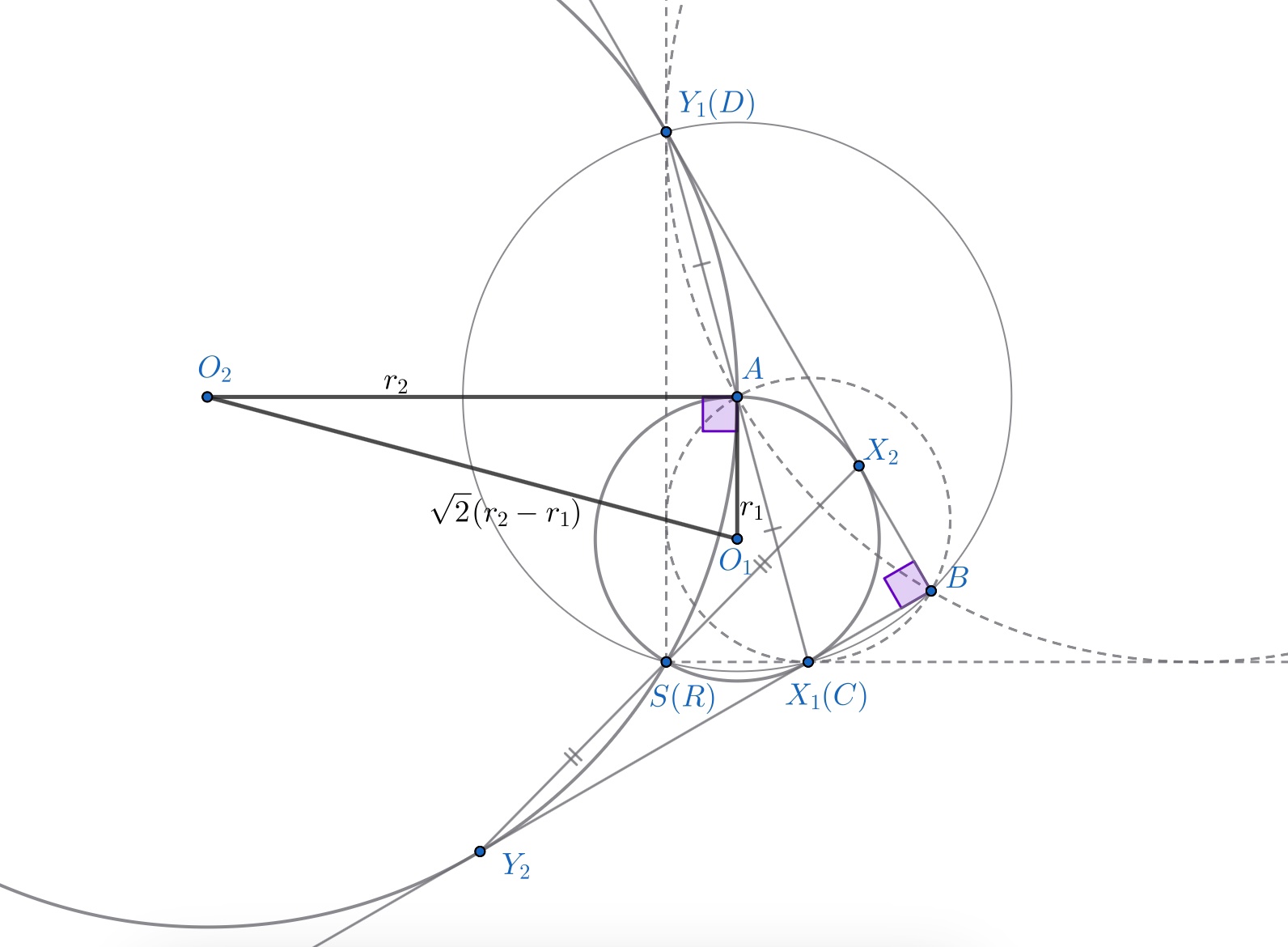
Вычислим отношение их радиусов — это легко делается применением теоремы Пифагора к треугольнику 
со сторонами
(здесь 
— центры новых окружностей, 
- радиусы). Получается 
; будем считать
.
Введём связанную с нашим прямым углом систему координат, тогда центры имеют координаты 
и 
, а точки
касания — 
. Середина 
— это 
, и, считая расстояния от неё до
и 
, убеждаемся, что это точка пересечения наших окружностей,как и середина 
. Значит, эти середины — точки 
.
Поскольку 
не лежит на биссектрисе угла, то прямая, из которой наш угол высекает отрезок с серединой 
, единственна, так что
соответствующая пара точек 
совпадает с парой 
.
_________________________________________________________________________________________________________________________________________________________________________________
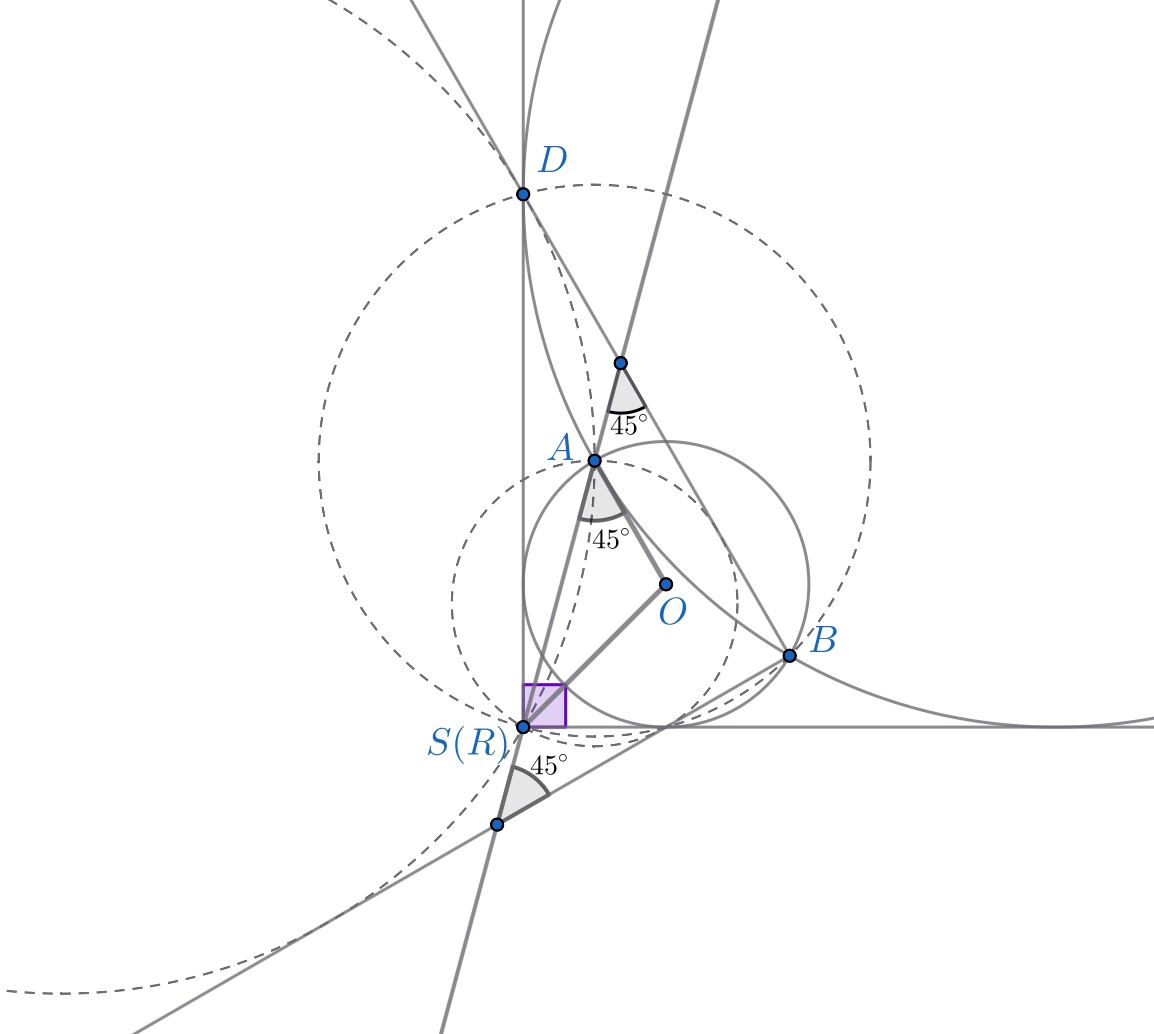
4. Исполним ту же самую инверсию, что и в предыдущем пункте, вновь получим прямой угол и вписанную в него пару окружностей.
Прямая 
пересекает стороны угла под 45 градусов, значит, то же делает эта же прямая 
с исходными
окружностями. Поэтому и угол 
( 
— центр меньшей окружности) равен 
.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
