16 Задания СтатГрада
Ошибка.
Попробуйте повторить позже
В лаборатории есть незаряженный плоский с квадратными пластинами. Площадь каждой его пластины см2, а расстоянием
между ними очень мало. В некоторый момент одной пластине сообщили заряд
мкКл, а другой – заряд
мкКл.
Найдите установившееся значение модуля напряженности электрического поля между первой и второй пластинами
конденсатора.
Источники:
Принцип суперпозиции электрических полей гласит, что напряжённость поля системы зарядов равна векторной сумме
напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности.
Поэтому результирующее напряженность в конденсаторе равна
где - вектор напряженность левой пластинки;
- вектор напряженность правой пластинки.
В нашем случае вектора напряженностей направлены навстречу друг другу, поэтому
Поскольку размеры пластин много больше расстояния между ними, можем пренебречь краевыми эффектами.
Ёмкость конденсатора вычисляется по формуле
где ;
- площадь пластинок;
- расстояние между пластинками.
Напряжение на конденсаторе равно
Тогда напряженность равна
Тогда напряженность одной пластинки .
В нашем случае
Тогда
Ошибка.
Попробуйте повторить позже
В лаборатории есть незаряженный плоский с квадратными пластинами. Площадь каждой его пластины см2, а расстоянием
между ними очень мало. В некоторый момент одной пластине сообщили заряд
мкКл, а другой – заряд
мкКл.
Найдите установившееся значение модуля напряженности электрического поля между первой и второй пластинами
конденсатора.
Источники:
Принцип суперпозиции электрических полей гласит, что напряжённость поля системы зарядов равна векторной сумме
напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности.
Поэтому результирующее напряженность в конденсаторе равна
где - вектор напряженность левой пластинки;
- вектор напряженность правой пластинки.
В нашем случае вектора напряженностей направлены навстречу друг другу, поэтому
Поскольку размеры пластин много больше расстояния между ними, можем пренебречь краевыми эффектами.
Ёмкость конденсатора вычисляется по формуле
где ;
- площадь пластинок;
- расстояние между пластинками.
Напряжение на конденсаторе равно
Тогда напряженность равна
Тогда напряженность одной пластинки .
В нашем случае
Тогда
Ошибка.
Попробуйте повторить позже
В теплоизолированном цилиндре объёмом л под поршнем находится 1 моль идеального одноатомного газа – неона – под
давлением
Па. Затем поршень сдвигается, и газ совершает работу
Дж. Найдите изменение среднеквадратичной
скорости теплового движения атомов неона в данном процессе.
Источники:
Запишем уравнение Менделеева-Клайперона
где - количества вещества;
- газовая постоянная.
Внутренняя энергия одноатомного газа вычисляется по формуле
Объединяя (1) и (2), получим
Средняя кинетическая энергия теплового движения атомов одноатомного газа равна
где - молярная масса вещества.
Объединяя (3) и (1) и учитывая, что , получим
Поскольку газ находится в теплоизолированном сосуде, то рассматриваемый процесс можно считать адиабатическим. Согласно первому закону термодинамики
где - работа газа.
Тогда
Тогда средняя кинетическая энергия теплового движения во втором состоянии равна
Тогда, учитывая, что для неона
Подставляя численные значения, получим
Ошибка.
Попробуйте повторить позже
Входной колебательный -контур радиоприёмника, служащий для выделения из радиоэфира сигналов с определёнными
частотами
, состоит из конденсатора и катушки индуктивности, содержащей
одинаковых параллельных витков. Модуль
вектора индукции магнитного поля каждого витка прямо пропорционален силе тока, протекающего через виток. Витки расположены
так близко друг к другу, что линии индукции поля, создаваемого одним витком, пронизывают всю катушку. Вначале контур был
настроен на приём радиопередач на частоте
МГц. Затем часть витков катушки закоротили, и полное число её витков
уменьшилось до
. Как и на сколько при этом изменилась частота принимаемых сигналов? Можно считать, что в катушке
индуктивности магнитные поля каждого витка с током одинаковы, и полный магнитный поток проходит через каждый
виток.
Источники:
Магнитный поток через катушку индуктивность выражается формулой
где - индуктивность катушки;
- сила тока через катушку.
Из условия следует, что магнитная индукция поля равна
где - коэффициент пропорциональности.
По принципу суперпозиции индукция магнитного поля катушку с витками равна
Магнитный поток катушки выражается формулой
Приравнивая (1) и (2), получим
Запишем формулу Томсона для периода колебаний -контура
где - ёмкость конденсатора.
А частота колебаний есть
Тогда
То есть, частота принимаемых сигналов увеличится на .
Ошибка.
Попробуйте повторить позже
Входной колебательный -контур радиоприёмника, служащий для выделения из радиоэфира сигналов с определёнными длинами
волн
, состоит из конденсатора и катушки индуктивности, содержащей
одинаковых параллельных витков. Модуль вектора
индукции магнитного поля каждого витка прямо пропорционален силе тока, протекающего через виток. Витки расположены так
близко друг к другу, что линии индукции поля, создаваемого одним витком, пронизывают всю катушку. Вначале контур был
настроен на приём радиопередач с длиной волны
м. Затем часть витков катушки закоротили, и полное число её витков
уменьшилось до
. Как и на сколько при этом изменилась длина волны принимаемых сигналов? Можно считать, что в
катушке индуктивности магнитные поля каждого витка с током одинаковы, и полный магнитный поток проходит через каждый
виток.
Источники:
Магнитный поток через катушку индуктивность выражается формулой
где - индуктивность катушки;
- сила тока через катушку.
Из условия следует, что магнитная индукция поля равна
где - коэффициент пропорциональности.
По принципу суперпозиции индукция магнитного поля катушку с витками равна
Магнитный поток катушки выражается формулой
Приравнивая (1) и (2), получим
Запишем формулу Томсона для периода колебаний -контура
где - ёмкость конденсатора.
Длина волны выражает из периода колебаний через следующую формулу
Тогда
То есть, длина волны принимаемых сигналов уменьшится на .
Ошибка.
Попробуйте повторить позже
В электрической цепи, схема которой изображена на рисунке, источник имеет ЭДС В и внутреннее сопротивление
Ом.
Сопротивления резисторов равны
Ом,
Ом,
Ом. Найдите силу тока
, который течёт через резистор
.
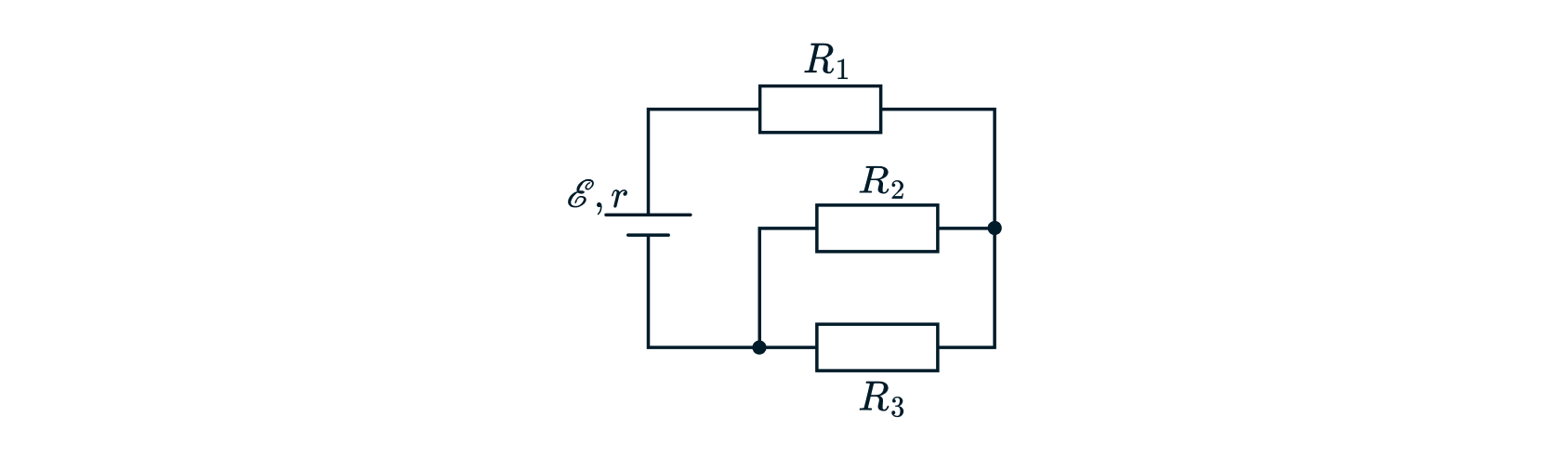
Источники:
Найдем общее сопротивление цепи. Поскольку резисторы и
соединены параллельно, то
А эквивалентный резистор соединен последовательно с
. Тогда
Тогда по закону Ома для полной цепи сила ток, протекающая в цепи, равна
Обозначим за и
токи через резисторы
и
, соответственно.
Тогда
Также поскольку резисторы и
соединены параллельно, то верно следующее равенство
Решая систему, состоящую из уравнений (1) и (2), получим
Ошибка.
Попробуйте повторить позже
В электрической цепи, схема которой изображена на рисунке, источник имеет ЭДС В и внутреннее сопротивление
Ом.
Сопротивления резисторов равны
Ом,
Ом,
Ом. Найдите силу тока
, который течёт через резистор
.
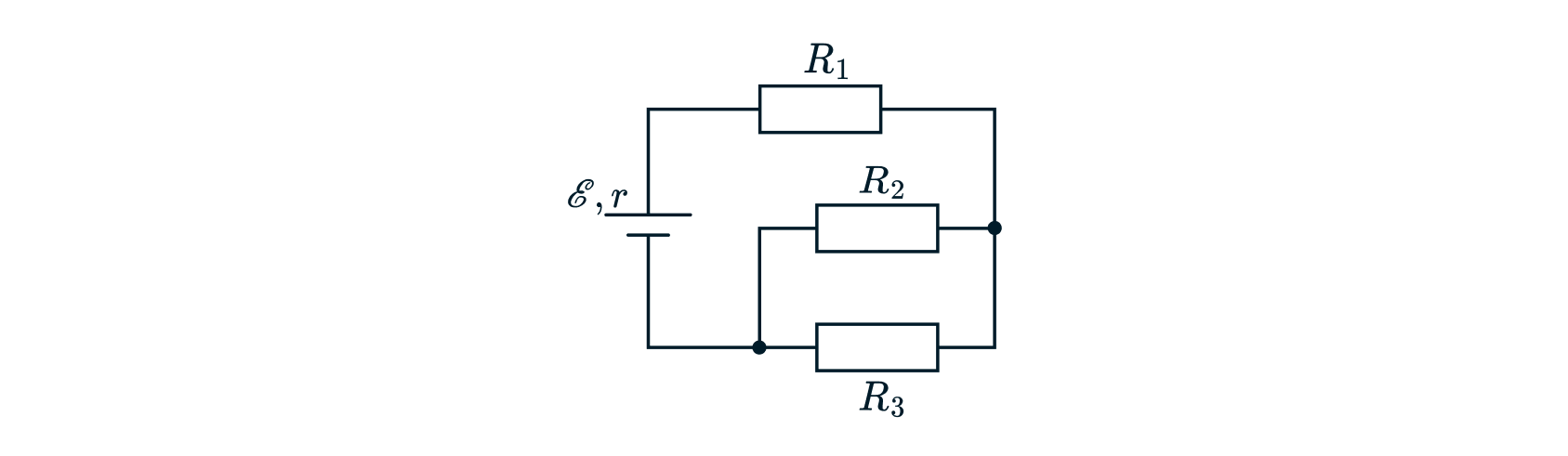
Источники:
Найдем общее сопротивление цепи. Поскольку резисторы и
соединены параллельно, то
А эквивалентный резистор соединен последовательно с
. Тогда
Тогда по закону Ома для полной цепи сила ток, протекающая в цепи, равна
Обозначим за и
токи через резисторы
и
, соответственно.
Тогда
Также поскольку резисторы и
соединены параллельно, то верно следующее равенство
Решая систему, состоящую из уравнений (1) и (2), получим
Ошибка.
Попробуйте повторить позже
В радиоприёмнике коротковолнового диапазона, настроенном на приём длины волны м, ёмкость конденсатора входного
контура
пФ. В некоторый момент времени амплитуда колебаний силы тока в контуре была равна
мА. Какова
была при этом амплитуда
колебаний напряжения на конденсаторе?
Источники:
По формуле Томсона период электромагнитных колебаний в идеальном колебательном контуре
где - индуктивность катушки.
Длина волны, принимаемой приемник
где - скорость света.
По закону сохранения энергии


