Тема СПБГУ - задания по годам

СПБГУ 2020

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела спбгу - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#72107

Какое наибольшее количество натуральных чисел от $1$ до $2500$ можно покрасить в желтый цвет так, чтобы произведение любых двух желтых чисел не было желтым?

Подсказки к задаче

Подсказка 1

Давайте сначала построим пример, а потом попробуем сделать оценку) Какими хочется видеть жёлтые числа, чтобы с легкостью сказать, является ли их произведение жёлтым?

Подсказка 2

Обратите внимание на то, что числа у нас ограничены по величине.

Подсказка 3

Если сделать жёлтые числа достаточно большими, то и произведение будет слишком большим! Отсюда мы можем построить предполагаемый пример ;)

Подсказка 4

После построения предполагаемого примера мы видим, что "запрещено" чисел не так уж и много! Работать сразу на большом множестве чисел неудобно, давайте попробуем разбить на группы, где нам будет удобно "запретить" красить некоторое количество чисел.

Подсказка 5

Нам нужны такие тройки, где мы сможем запретить по числу ;)

Показать ответ и решение

Заметим, что единица не окрашена, так как $1⋅1= 1.$ Кроме того, в паре $(50,2500)$ одно из чисел не окрашено. Рассмотрим набор чисел $2 2 2 2 2 2,3,...,49;51,52,...,98;50 − 48,50 − 47 ,...,50 − 1.$ Все эти числа различны, так как $2 2 50− 48 = 98 ⋅2 >98.$ Разобьём их на тройки вида $2 2 (50− n,50+ n,50 − n ),$ где $n ∈[1;48].$ Поскольку $2 2 (50− n)(50+ n)=50 − n ,$ в каждой тройке есть хотя бы одно неокрашенное число, а всего имеется $48$ таких троек. Таким образом, мы нашли $50$ неокрашенных чисел, поэтому количество жёлтых чисел не превосходит $2450.$

Покажем, что эта оценка реализуется. Покрасим все числа от $51$ до $2500.$ Такая раскраска нам подходит, поскольку произведение любых двух жёлтых чисел больше $2500.$

Ответ:

$2450$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#73688

Даны натуральные числа от $1$ до $2040,$ причем $n$ чисел покрашены в зеленый цвет. При каком наибольшем $n$ может оказаться так, что ни одна степень двойки не покрашена и не представима в виде суммы двух зеленых чисел?

Подсказки к задаче

Подсказка 1

К нашему множеству достаточно близко находится число 2048, являющееся одиннадцатой степенью двойки, а его половина, 1024, находится почти посередине данного множества. Можно ли как-то числа данного множества на пары так, чтобы их сумма была 2048?

Подсказка 2

Конечно, все числа разбить не выйдет, но можно выделить пары: 1024 - k и 1024 + k для k от 1 до 1016, в которых хотя бы одно число не окрашено. А какие из чисел, не попавших ни в какую пару, тоже не окрашены?

Подсказка 3

Конечно! По аналогичным причинам (1,7), (2,6) и (3,5) имеют неокрашенное число, а числа 4 и 1024 по условию не окрашены. Тогда выходит, что n не превосходит 1019. А как можно привести пример?

Подсказка 4

Между соседними степенями двойки достаточно быстро увеличивается расстояние при увеличении степеней. Можно ли большинство чисел окрасить так, чтобы их сумма находилась между какими-то соседними степенями двойки?

Показать ответ и решение

Рассмотрим пары вида $(1024− k,1024+ k)$ где $k∈1,2,...,1016.$ В каждой паре имеется хотя бы одно непокрашенное число, поскольку $11 (1024− k)+ (1024+k)= 2 .$

Аналогичным образом получается, что пары $(1,7),(2,6),(3,5)$ содержат не менее трех непокрашенных чисел. Наконец, числа $4$ и $1024,$ не попавшие ни в одну из пар, по условию тоже не окрашены. Таким образом, имеется не менее $1021$ непокрашенных чисел, откуда $n ≤1019.$

Покажем, что полученная оценка реализуется. Покрасим числа $5,6,7,$ а также все числа от $1025$ до $2040.$ Пусть $m$ и $n$ — зеленые числа. Нам достаточно проверить, что $m + n$ не является степенью двойки. Если $m, n< 8$ то это очевидно. В случае $m,n> 1024$ мы получаем $11 12 2 =2048< m+ n≤ 2040+2040= 4080< 4096= 2 .$

Наконец, если $m< 8$ и $n> 1024,$ то $1024< m +n < 2048.$

Ответ:

$1019$

Ошибка.
Попробуйте повторить позже

Задача 3#81492

Какое наибольшее количество нечетных натуральных чисел от $1$ до $3600$ можно покрасить в черный цвет, чтобы нельзя было выбрать такую тройку различных черных чисел $a,b$ и $c,$ что $a$ делится на $b$ и $b$ делится на $c?$

Подсказки к задаче

Подсказка 1

Попробуйте разбить возможные значения нечётных чисел, меньших либо равных 3600, на семейства.

Подсказка 2

Например, можно рассмотреть n, не кратные 3.

Подсказка 3

Попробуйте в качестве примера придумать геометрическую прогрессию.

Подсказка 4

Нам может пригодиться такая прогрессия для n, не кратного 3: n, 3n, ... , 3ᵏn.

Подсказка 5

Посчитайте, сколько всего есть таких прогрессий, обратите внимание на первый член.

Показать ответ и решение

Для любого нечётного $n ≤3600,$ не кратного $3,$ рассмотрим геометрическую прогрессию $n,3n,32n,...,3tn.$ Очевидно, что прогрессии, у которых различные первые члены, не имеют общих членов. Также отметим, что любое число от $1$ до $3600$ входит в какую-то прогрессию.

Всего существует $1200$ таких прогрессий и $800$ из них имеют первый член, больший $1200.$ По условию в прогрессии может быть не более двух чёрных чисел. В прогрессий, у которой первый член больше $1200,$ не более одного чёрного числа (потому что их вторые члены уже больше $3600$ ). Поэтому, всего не более $(1200− 800)⋅2+ 800= 1600$ чёрных чисел.

Предъявим пример: покрасим все нечётные числа между $400$ и $3600.$ Предположим, что нашлись такие чёрные числа $a,b,c,$ что $.. a.b$ и $.. b.c,$ тогда $a≥ 3b≥ 9c≥ 9⋅401= 3609> 3600,$ поскольку числа нечётные, противоречие.

Ответ:

$1600$

Ошибка.
Попробуйте повторить позже

Задача 4#96341

Какое наименьшее количество натуральных чисел от $1$ до $320$ нужно покрасить в красный цвет, чтобы $1$ и $320$ были красными, а также для любого красного числа $a,$ большего $1,$ нашлись такие красные числа $b$ и $c$ (возможно, одинаковые), что $a =b+ c?$

Подсказки к задаче

Подсказка 1

Скажем, что мы закрасили числа a₁, a₂, ... , aₙ. Упорядочим их по возрастанию.

Подсказка 2

Запишите отношение между aᵢ и aᵢ₋₁.

Показать ответ и решение

Пусть окрашено $n$ чисел. Упорядочим их по возрастанию:

1= a1 < a2 < ...< an = 320

Заметим, что для любого $k∈ {2,...,n}$ справедливо неравенство

a ≤2a k k−1

Действительно, в противном случае при $i,j <k$ , имеем

a > 2a ≥ a + a k k−1 i j

и мы не сможем представить $ak$ в виде суммы двух красных чисел. Тогда

320= an ≤ 2an−1 ≤4an−2 ≤ ...≤ 2n− 1a1 = 2n−1

Значит, $n− 1≥ 9$ и $n ≥10$ . Осталось привести пример покраски 10 чисел: $1,2,4,5,10,20,40,80,160,320$ .

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 5#103213

Даны числа $x,y,z ∈ [0,π]. 2$ Найдите максимальное значение выражения

3∘------- 3∘ ------- √3------- A = sinx cosy+ sinycosz+ sinzcosx.

Источники: СПБГУ - 2020, 11.2 (см. olympiada.spbu.ru)

Подсказки к задаче

Подсказка 1

Вспомним, что куб суммы трёх слагаемых не может быть больше суммы кубов соответствующих слагаемых, домноженной на 9. Распишем так наше выражение и посмотрим повнимательнее! Было бы очень удобно от произведения синусов и косинусов прийти к их квадратам, чтобы воспользоваться основным тригонометрическим тождеством, но как это сделать....

Подсказка 2

Конечно, можно записать, что произведение синуса и косинуса не превосходит полусумму квадратов по неравенству Коши для средних!

Подсказка 3

Теперь можем легко найти значение куба числа А! Остаётся только выразить отсюда само А и подобрать подходящие x, y и z.

Показать ответ и решение

Первое решение.

Воспользуемся неравенством

3 ( 3 3 3) (a+ b+ c) ≤ 9 a +b + c при a,b,c≥ 0.

Тогда с учетом неравенства Коши для средних

3 9 ( 2 2 2 2 2 2 ) 27 A ≤ 9(sin xcosy+ sinycosz+ sinzcosx)≤ 2 sin x +cos y+sin y +cosz +sin z +cosx = -2

откуда $3 A ≤ 3√2.$ Равенство реализуется при $π x= y = z = 4.$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Заметим, что для любого $t$

√ - ( ) √- sin t+cost= 2⋅sin t+ π ≤ 2. 4

В силу неравенства Коши для средних

√ -------- ∘ ---------√-- √- √36-⋅ 3 sinu⋅cosv =3 3sinu ⋅cosv⋅-22-≤sinu+ cosv+-22-. 2

Применим эту оценку при $(u,v)∈{(x,y),(y,z),(z,x)}$ и затем сложим получившиеся неравенства. Тогда

√- √- √- 3A- 3-2 √- 3-2 9-2 6√2 ≤sin x+ cosx+ siny+ cosy +sin z+cosz+ 2 ≤ 3 2+ 2 = 2 ,

откуда $3-- A ≤ 3√2.$ Равенство реализуется при $π x= y = z = 4.$

Ответ:

$-3√- 32$

Ошибка.
Попробуйте повторить позже

Задача 6#103215

В восьмеричной системе $x= 344344...344,$ где блок $344$ повторяется $n$ раз. Восьмеричное число $y$ получается из $x$ некоторой перестановкой цифр. Оказалось, что восьмеричная запись $x ⋅y$ равна $2020...20.$ При каких $n$ это возможно?

Источники: СПБГУ - 2020, 11.4 (см. olympiada.spbu.ru)

Подсказки к задаче

Подсказка 1

В условии даны x и xy, значит, верный путь найти y — поделить xy на x. А проще всего это сделать в десятичной системе счисления!

Подсказка 2

Зная количество знаков в записи x и записи y, мы можем сказать, сколько знаков в записи xy. Теперь у нас есть всё необходимое, чтобы перевести все вычисления в десятичную систему. Чему же равен y?

Подсказка 3

y = 292 * (8^(3n) + 1) / 513. Давайте заметим, что 513 = 8^3 + 1. Попробуйте разложить верхнюю скобку в телескопическую сумму так, чтобы можно было сократить на 513. А на 292 пока можно не обращать внимания — ведь умножить мы всегда успеем.

Подсказка 4

Можно разложить на сумму разностей вида 8^(3n) - 8^(3(n-1)). Получилась странное выражение, но попробуйте записать это число в восьмеричной системе счисления! Сразу понятно, что всё проделанное не зря.

Подсказка 5

Получилось число с повторяющимся блоком 777000. Теперь можно и на 292 домножить — и получится искомый вид числа y!

Подсказка 6

Чтобы найти n, осталось лишь посчитать количество троек в x и в y, ведь количество повторяющихся блоков мы считать умеем. И не забудьте привести пример!

Показать ответ и решение

Договоримся восьмеричные числа писать в скобках, чтобы отличать их от десятичных. Запись $xy$ содержит $3n$ блоков вида $20,$ поэтому

( ) 643n − 1 (83n− 1)(83n+ 1) xy = 16⋅1 +64+ 642 +...+ 643n−1 = 16⋅-63---= 16 ⋅-----7⋅9------.

Кроме того, $(344)= 228,$ откуда

( ) 3n x =228⋅ 1+ 83+86+ ...+ 83(n−1) =228⋅ 8-−-1= 3⋅4⋅19⋅(83n − 1). 511 7⋅73

Поделив первое равенство на второе, мы получим

( ) y = xy=-4⋅73-⋅(83n +1)= 292⋅-83n+-1-. x 27⋅19 513

Так как $292$ и $513$ взаимно просты, на $513$ должно делиться число $83n +1$ , поэтому $n$ нечётно. Заметим, что

83n+ 1 ( 3(n−1) 3(n−2)) (6 3) --513--= 8 − 8 + ...+ 8 − 8 +1= (777000...777000777001),

где блок $777$ повторяется $n−21$ раз. Поскольку $292 =(444)$ и

(777)⋅(444)= (1000)⋅(444)− (444)= (444000)− (444)= (443334),

мы получаем:

y = (443334...443334444),

где блок из троек повторяется $n−1 2$ раз. Таким образом, в восьмеричную запись $y$ входит $3(n − 1) 2$ троек. С другой стороны, запись числа $x$ содержит $n$ троек. Поэтому $3(n − 1)= n, 2$ откуда $n= 3.$ При $n = 3$ нам подходит число $y =(443334444).$

Ответ:

$n =3$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#103216

В школе $2019$ учеников. В один прекрасный день некоторые из них поздоровались друг с другом за руку, причем из любой тройки учеников хотя бы двое не здоровались. При каком наибольшем $k$ могло оказаться так, что для любого $n,$ не превосходящего $k,$ найдется школьник, поздоровавшийся ровно с $n$ учениками?

Источники: СПБГУ - 2020, 11.5 (см. olympiada.spbu.ru)

Подсказки к задаче

Подсказка 1

Попробуйте зафиксировать ученика A и посмотреть, с кем он поздоровался (множество B). Что можно сказать про этих ребят?

Подсказка 2

Они не здоровались друг с другом! Отлично, у мы можем оценить количество тех, с кем они общались, кроме A.

Подсказка 3

Рассмотрите человека, который здоровался менее k раз. Пусть он поздоровался m раз. Можно ли оценить с помощью его знакомств общее количество человек?

Подсказка 4

Всего человеке не меньше, чем k+m! А как применить условие на k?

Подсказка 5

Есть люди, которые здоровались с m+1, m+2, ..., k-1 людьми! Могут ли они быть людьми из множества B? Как оценить количество человек с другой стороны?

Подсказка 6

Учеников в школе не меньше, чем 2k-m! Каким тогда может быть k?

Показать ответ и решение

Предположим, что школьник $A$ поздоровался с учениками $B ,...,B . 1 k$ По условию ни при каких $i$ и $j$ школьники $B i$ и $B j$ не здоровались друг с другом. Рассмотрим всех учеников, которые поздоровались менее $k$ раз, и выберем среди них того, кто здоровался не меньше других. Будем для определенности считать, что это $B1$ и что он поздоровался $m$ раз. Тогда кроме $A$ школьник $B1$ поздоровался еще с некоторыми учениками $C1,C2,...,Cm −1$ . Значит, в школе не менее $(k+ 1)+(m − 1)= k+ m$ учеников.

С другой стороны, по условию есть ученики, поздоровавшиеся ровно с

m + 1,m + 2,...,k− 1

школьниками, и они не находятся среди $A,B1,...,Bk.$ Поэтому учеников в школе не меньше, чем

(k+1)+ (k− 1 − m )=2k− m.

Таким образом, справедливы неравенства

2019 ≥k +m, 2019 ≥2k− m.

Складывая их, мы получим

4038- 4038≥(k+ m)+ (2k − m )= 3k =⇒ k≤ 3 = 1346

Покажем теперь, что $k= 1346$ реализуется. Разобьём всех учеников на две групшы: $A1,...,A673$ и $B1,...,B1346.$ Пусть $Ai$ поздоровался с $Bj$ при $i≤ j,$ а остальные пары школьников не здоровались друт с другом. Проверим, что такой пример нам подходит.

Первое условие задачи выполнено, поскольку в любой тройке учеников найдутся двое из одной группы, а они между собой не здоровались. Возьмем $n ∈{1,...,1346}$ . Если $n> 673,$ то число $i= 1347− n$ не превосходит $673.$ Тогда ученик $Ai$ поздоровался ровно с $1346− i+1= n$ школьниками. Если же $n≤ 673,$ то ученик $Bn$ поздоровался со школьниками $A1,...,An,$ которых ровно $n.$ Таким образом, и второе условие задачи выполнено.

Ответ:

$k =1346$

Ошибка.
Попробуйте повторить позже

Задача 8#103217

Две правильные треугольные пирамиды имеют общую боковую грань и не имеют других общих точек. В пирамиды вписаны шары радиуса $r.$ Третий шар радиуса $R$ касается внешним образом обеих пирамид и вписанных в них шаров. Найдите плоский угол при вершине пирамид, если $R :r= 2:1.$

Источники: СПБГУ - 2020, 11.6 (см. olympiada.spbu.ru)

Подсказки к задаче

Подсказка 1

Пусть O₁ и O₂ - центры вписанных сфер, а O — центр внешней сферы. Рассмотрите треугольник OO₁O₂, из него можно получить много информации.

Подсказка 2

Ну, во-первых, он равнобедренный. Во-вторых, вы можете выразить его стороны через радиусы. В-третьих, попробуйте рассмотреть точки K — середину O₁O₂, M — точка касания сферы и одной из пирамид и точку N касания вписанных сфер. Что можно сказать про угол MNK и чему он равен?

Подсказка 3

Это угол между боковыми гранями пирамиды. Кстати, почему? Пусть боковое ребро пирамиды равно a. Используя величину угла, вы сможете выразить длину ребра основания через a, если проведёте высоты в двух боковых гранях к одному ребру. А там и до плоского угла при вершине недалеко.

Показать ответ и решение

Пусть $SABC$ — первая пирамида, $BSC$ — её общая боковая грань со второй, $O 1$ и $O 2$ — центры шаров, вписанных в пирамиды, $O$ — центр внешнего шара. Ввиду равенства пирамид вписанные в них шары касаются грани $BSC$ в одной точке $K.$ Так как $O1K ⊥BSC$ и $O2K ⊥ BSC,$ точка $K$ лежит на отрезке $O1O2,$ причём $O1O2 = 2r.$

Пусть $M$ — точка касания с гранью $ASB$ шара, вписанного в первую пирамиду. В этой же точке касается $ASB$ и внешний шар. Поэтому точка $M$ лежит на отрезке $OO1,$ причём $OO1 =r +R.$ Аналогично получается, что $OO2 = r+R.$ Выберем точку $N$ на отрезке $OK$ так, что $NM ⊥ OO1,$ и положим $φ= ∠MNK.$

$PIC$

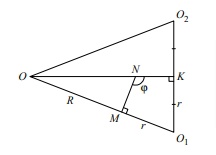
Тогда

( ) O1K = OO1 ⋅cos∠OO1K ⇐⇒ r=(r+ R)⋅cos(π− φ)⇐⇒ R = −r --1-+ 1 . cosφ

По условию $R =2r,$ откуда $1 cosφ =− 3.$

Покажем, что $φ$ — угол между гранями $ASB$ и $BSC.$ Действительно, $O1K$ и $O1M$ — радиусы шара, вписанного в первую пирамиду, откуда $O1M ⊥ ASB$ и $O1K ⊥ BSC.$ Значит, $BS ⊥MNK.$ Кроме того, прямая $MN$ лежит в плоскости $ASB$ , а $KN$ — в плоскости $BSC.$

$PIC$

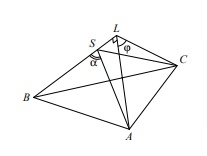
Пусть $α= ∠ASB,a= AB.$ Опустим из точек $A$ и $C$ перпендикуляры на ребро $BS.$ Они придут в одну точку $L,$ так как треугольники $ASB$ и $BSC$ равны. По доказанному $∠ALC = φ.$ Заметим, что