Тема ДВИ в МГУ - задания по годам

ДВИ 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дви в мгу - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 21#92118Максимум баллов за задание: 7

В основании прямой призмы лежит ромб со стороной 3. Найдите объём призмы, если известно, что существует сфера радиуса 1, касающаяся плоскости нижнего основания, двух противоположных боковых рёбер и всех рёбер верхнего основания.

Источники: ДВИ - 2024, вариант 243, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Построим чертёж! Проведите перпендикуляры из центра сферы к параллельным между собой боковым рёбрам (в точки касания). Что можно сказать о фигуре, образованной диагональю ромба, частями этих рёбер и проведёнными перпендикулярами?

Подсказка 2

Теперь мы знаем диагональ ромба! Это позволяет нам полностью обсчитать ромб, найти его углы/высоту/площадь и всё что нам нужно!

Подсказка 3

Спроецируем радиус сферы, проведённый в точку касания её с ребром верхнего основания, на плоскость основания. Эта проекция — половина высоты ромба.

Подсказка 4

Работа с теоремой Пифагора поможет нам отыскать оставшуюся часть высоты призмы. Осталось подставить числа в формулу и записать ответ.

Показать ответ и решение

Пусть дана призма $ABCDA ′B′C′D′,$ $O$ — центр данной сферы, которая касается боковых рёбер $BB′$ и $DD ′$ в точках $K$ и $L.$

Заметим, что $′ OK ⊥ BB$ и $′ OL ⊥ DD ,$ следовательно $′ KL ⊥ BB .$ А раз $′ BB ⊥ BD$ и все четыре точки $B,K,L,D$ лежат в одной плоскости, то $KL ∥KL$ и $BKLD$ — прямоугольник, значит, $BD =KL,$ при этом $KL = 2$ как диаметр данной сферы.

Рассмотрим треугольник $ABD$ и найдём высоту $DH.$ По формуле Герона $√- SABD = 2 2,$ тогда

1 SABD = 2DH ⋅AB

√- 3DH = 2 2 2

√ - DH = 4-2 3

Проецируем $O$ на нижнее основание, обозначим проекцию на $Q,$ она будет являться серединой $BD.$ Пусть $G$ — точка касания сферы с $A′B ′,$ а $E$ — её проекция на нижнее основание.

$PIC$

Раз $OG ⊥A ′B′$ , то в силу ТТП и свойств проекции $QE ⊥ AB.$ Тогда $QE$ — средняя линия в треугольнике $BDH,$ следовательно $√ - QE = 1DH = 2--2. 2 3$

Рассмотрим прямоугольную трапецию $GOQE,$ в ней $OG =OQ = 1$ и $2√2 QE = -3-.$ Пусть $GE = h,$ тогда по теореме Пифагора

(GE − OQ)2+ QE2 = OG2

(h− 1)2 + 89 = 1

h = 4 3

Теперь зная это, посчитаем объём призмы

- - 4√2 4 16√2 V =SABCD ⋅GE = AB⋅DH ⋅GE = 3⋅ 3 ⋅3 = 3

Ответ:

$16√2 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 22#92257Максимум баллов за задание: 7

Дана функция

(x+-1)2+-x2 f(x)= (x+ 1)2− x2.

Найдите наибольшее целое число, не превосходящее числа $f(2024)$ .

Источники: ДВИ - 2024, вариант 244, задача 1 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Если раскрыть квадраты суммы, то f(x) представима в виде (многочлен 2 степени)/(многочлен 1 степени). Как это можно упростить?

Подсказка 2

Поделить многочлены с остатком! Можно либо поделить в столбик, либо самому разбить дробь на две более простые так, чтобы одна из дробей сократилась со знаменателем

Показать ответ и решение

Преобразуем функцию по аналогии с выделением целой части у дроби:

2x2+-2x-+1- x(2x+-1)+x-+1- x+-1- f(x)= 2x+ 1 = 2x +1 =x + 2x +1

Тогда

2025 f(2024)= 2024+ 4049

Так как второе слагаемое меньше $1,$ то наибольшее не превосходящее $f(2024)$ целое число это $2024.$

Ответ: 2024

Ошибка.
Попробуйте повторить позже

Задача 23#92258Максимум баллов за задание: 7

Вычислите сумму

-11-- --11--- ----11---- -----11------ 1+2 + 1+2 +3 +1 +2+ 3+ 4 + ...+ 1+ 2+...+10.

Источники: ДВИ - 2024, вариант 244, задача 2 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Какую закономерность можно заметить в знаменателях у слагаемых суммы? Можно ли её посчитать?

Подсказка 2

Знаменатель каждого из слагаемых представляет собой сумму членов арифметической прогрессии! Попробуйте расписать ее для произвольного k-го слагаемого

Подсказка 3

Полученная дробь разбивается на разность двух более простых дробей. (Разбиение нетрудно подобрать руками, но можно его найти и через метод неопределенных коэффициентов)
Теперь вместо каждого слагаемого суммы подставляем его представление через разность дробей. Что получим?

Подсказка 4

Благополучно почти все дроби сократятся! Остается посчитать разность двух дробей

Показать ответ и решение

По формуле суммы арифметической прогрессии каждый знаменатель имеет вид $1+ ...+ k= k(k+1). 2$ Отсюда получаем, что каждое слагаемое можно представить в виде

22 k +1− k ( 1 1 ) k(k+-1) =22-k(k+-1) =22 k − k+-1

Тогда искомая сумма равна

( ) 22 1 − 1+ 1− 1+ ...+ -1− -1 = 2 3 3 4 10 11

( ) = 22 1− -1 = 11− 2= 9 2 11

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 24#92259Максимум баллов за задание: 7

Решите неравенство

( 1) ( 1) log9 x + 3 − log3 x− 3 ≥ 1.

Источники: ДВИ - 2024, вариант 244, задача 3 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Перед нами логарифмическое неравенство. Что делаем первым делом?

Подсказка 2

Записываем ОДЗ, конечно! Теперь на этом множестве можем совершать преобразования. Как будем действовать?

Подсказка 3

Основание первого логарифма является квадратом основания второго логарифма! Можем по свойству логарифмов вынести этот квадратик ;)

Подсказка 4

Чтобы избавиться от неприятного множителя 1/2, мы можем просто домножить обе части неравенства на 2. Тогда у второго логарифма появится коэффициент 2, который уже можем занести в степень аргумента!

Подсказка 5

Получили разность логарифмов с одинаковыми основаниями. Победа! Теперь после преобразования разности логарифмов к логарифму частного мы получим элементарное логарифмическое неравенство!

Подсказка 6

Задача свелась к простому дробно-рациональному неравенству. Остается его решить классическим методом интервалов и не забыть про ОДЗ!

Показать ответ и решение

Выпишем ОДЗ:

{ x+ 1> 0 (1 ) x− 31> 0 ⇐⇒ x ∈ 3 ;+ ∞ 3

Умножим наше неравенство на $2,$ преобразуем выражения под знаком логарифма:

2 log (3x+-1)− 2log ( 3x-− 1) ≥ 2 9 3 3 3

(3x +1) log3 --3-- − 2(log3(3x − 1)− 1)≥2

log3(3x +1)− 1− 2 log3(3x− 1)+2 ≥2

( ) log3 -3x+-12 ≥1 =log33 (3x− 1)

Так как функция $log3t$ монотонно возрастает, то

--3x+1---≥ 3 9x2− 6x+ 1

Домножим на положительный (с учетом ОДЗ!) знаменатель:

2 3x+ 1≥27x − 18x +3

2 27x − 21x+ 2≤0

По обратной теореме Виета у квадратного трехчлена в левой части $19,23$ — все его корни. Тогда

[ 1 2] x∈ 9;3

Пересекая с ОДЗ, получаем ответ.

Ответ:

$(1;2] 3 3$

Ошибка.
Попробуйте повторить позже

Задача 25#92260Максимум баллов за задание: 7

Решите уравнение

tgx⋅tg2x cos2x+ 2 = 1.

Источники: ДВИ - 2024, вариант 244, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Явно напрягает произведение тангенсов. Давайте распишем их по определению и запишем условие их существование!

Подсказка 2

В итоге получим tg(x) * tg(2x)/2 = sin²(x)/cos(2x). После подстановки в уравнение мы можем обе части домножить на ненулевое число cos(2x)!

Подсказка 3

Получим классическое тригонометрическое уравнение. Если распишем косинус двойного угла через синус, то получим квадратное уравнение относительно него ;)

Подсказка 4

Остается соотнести полученные решения с условием существования исходных тангенсов!

Показать ответ и решение

Преобразуем второе слагаемое, но перед этим запомним, что оба тангенса должны быть определены:

tgx-⋅tg2x- sin-xsin2x- sin2x- 2 = 2cosxcos2x = cos2x

Тогда домножим наше уравнение на ненулевое число $cos2x.$ А также после замены $2 t=sin x$ получаем $cos2x= 1− 2t$ и квадратное уравнение

(1− 2t)2 +t= 1− 2t

1− 4t+ 4t2 +t= 1− 2t

2 1 4t − t =0, t= 0 или t= 4

cos2x =1 или cos2x= 1 2

x= πn;n ∈ℤ или 2x= ± π+ 2πn;n ∈ℤ 3

Ответ:

$πn;±π + πn;n ∈ℤ 6$

Ошибка.
Попробуйте повторить позже

Задача 26#92261Максимум баллов за задание: 7

В окружность $Ω$ вписан четырёхугольник $ABCD$ . На стороне $BC$ отмечена точка $E$ таким образом, что $CD = CE = 1$ и $∘ ∠AED =30$ . Найдите радиус окружности $Ω$ , если известно, что $∘ ∠ACD =25$ и $∘ ∠ACB = 75$ .

Источники: ДВИ - 2024, вариант 244, задача 5 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В условии нам даны углы и равные стороны, давайте тогда попробуем посчитать и другие!

Подсказка 2

∠DAB = 80°, а ∠CAE = 35°! Давайте теперь подумаем, а на что намекает нам поиск радиуса описанной окружности треугольников, в которых известны некоторые стороны и углы?

Подсказка 3

Будем пользоваться теоремой синусов! Было бы удобно для этого выбрать треугольники с известными углами и с общими сторонами.

Подсказка 4

Применим теорему синусов для треугольников △DCE, △ACD и выразим DE и AD через тригонометрические функции и ∠DAC! А в каком треугольнике мы можем связать эти две стороны с помощью пропорции?

Подсказка 5

Запишем пропорцию со сторонами AD и DE из теоремы синусов для треугольника △ADE! Теперь мы можем подставить раннее найденные представления этих сторон и выразить 2*sin(25).

Подсказка 6

2sin(25°) = sin(∠DAC)*2*cos(40°)/sin(∠DAC+35°). Осталось лишь найти, чему может быть равен ∠DAC и найти радиус известным ранее способом ;)

Показать ответ и решение

Первое решение.

$PIC$

$∠CDE = ∠CED = 40∘$ из треугольника $CDE,$ $∠CAE = 35∘$ из треугольника $CEA,$ $∠DAB = 80∘$ из вписанности четырёхугольника $ABCD.$

По теореме синусов для треугольника $DCE :$

--DE-- = --1-,DE = sin-80∘ =2cos40∘. sin100∘ sin40∘ sin 40∘

По теореме синусов для треугольника $ACD :$

----1---= -AD--,AD = -sin25∘-. sin∠DAC sin 25∘ sin∠DAC

Наконец, применяя теорему синусов для $ADE$ :

-AD-- -----DE------ sin 30∘ = sin(∠DAC +35∘).

Подставляем в последнюю пропорцию выражения для $AD$ и $DE$ , которые получили выше:

∘ sin∠DAC--⋅2-cos40∘ 2sin25 = sin(∠DAC +35∘) .

Отсюда видно, что $∠DAC =30∘$ подходит, т.к. $sin 65∘ = cos25∘$ , а из

sin50∘ sin(∠DAC + 35∘) sin25∘-= 2cos25∘ =---sin∠DAC----= cos35∘+ sin35∘ctg∠DAC.

понятно, что этот угол определяется однозначно (он лежит в интервале от $0$ до $π$ , и мы знаем численное значение его котангенса).

Таким образом, можно выразить радиус окружности из треугольника $DAC :$

R = 1⋅--1-∘ =1. 2 sin 30

______________________________________________________________________________________________________________________________________________________

Второе решение.

Посчитаем углы:

∠DCE =∠ACE +∠DCA =100∘

∘ ∠CDE =∠CED =40

∠EAC =180∘− ∠AEC − ∠ECA =35∘

Отметим на $AE$ такую точку $F,$ что $∠CF E =40∘ :$

$PIC$

Тогда $∠FCA =35∘,$ то есть $∠FCA = ∠EAC,$ откуда $F A= FC.$ А $∠EF C =70∘,$ то есть $∠EFC = ∠AEC,$ откуда $FC = EC = CD =1.$ Значит, треугольник $FDC$ равнобедренный, а так как $∠F CD =60∘,$ то $FDC$ ещё и равносторонний, то есть $FC = CD = FD.$

Итак, мы получили, что

FA =F D =FC = 1,

откуда точка $F$ является центром окружности, описанной около треугольника $ACD.$ Отсюда искомый радиус равен 1.

Ответ: 1

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 27#92262Максимум баллов за задание: 7

Многочлен $f(x)$ второй степени имеет действительные коэффициенты. Попарно различные действительные числа $a,b,c$ удовлетворяют условиям

f(a)= bc,f(b)= ca,f(c)=ab.

Найдите все возможные значения выражения

f(a)+-f(b)+-f(c) f(a+ b+c)

при условии, что $f(a +b+ c) ⁄=0$ .

Источники: ДВИ - 2024, вариант 244, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте запишем f(x) в явном виде. f(x) = dx² + ex + f, где d - ненулевой коэффициент! Теперь нужно как-то использовать условие на связь a, b, c.

Подсказка 2

Составим систему из 3х уравнений. Мы бы очень хотели восстановить все коэффициенты многочлена f(x). Что можно сделать?

Подсказка 3

Может помочь вычитание уравнений! Например, вычтем из второго первое и из третьего первое. В итоге красиво собираются коэффициенты: перед d — разность квадратов, перед e — разность этих же чисел, справа — число, помноженное на эту же разность!

Подсказка 4

Если расписать разность квадратов, то у каждого из слагаемых уравнения будет общий множитель ;) Поскольку a,b,c - различные, то мы без проблем можем обе части уравнения поделить на этот множитель!

Подсказка 5

В итоге получили систему из двух линейных уравнений относительно d и e. Можем решить ее аналогичным вычитанием!

Подсказка 6

После того, как нашли d и e, можем найти f путем подстановки известных коэффициентов в любое уравнение исходной системы.

Подсказка 7

Коэффициенты f(x) восстановлены! Теперь остается аккуратно подставить значения функции в выражение [f(a)+f(b)+f(c)]/f(a+b+c)

Показать ответ и решение

Пусть многочлен $f(x)$ имеет вид $dx2+ ex +f.$ Тогда выпишем условия:

( a2d +ae+ f = bc |{ 2 |( bd2+ be+ f = ca cd+ ce+ f = ab

Вычтем из второго уравнения первое, из третьего вычтем первое:

{ (b2− a2)d+ (b− a)e= c(a− b) (c2− b2)d+ (c − b)e =a(b− c)

Так как по условию все числа попарно различны, то получаем

{ (a +b)d+e =− c (c+ b)d +e= −a

Вычитая из верхнего нижнее:

(a− c)d= a− c, d= 1

Тогда

e= −a − b− c

f =bc− a(− a− b− c)− a2 = ab+ bc+ ac

Наконец, вычислим искомое

f(a)+f(b)+f(c) --f(a+-b+c)-- =

= -------2-----bc+-ca-+ab--------------= (a +b+ c)− (a+b+ c)(a+ b+ c)+ ab+bc+ ca

ab-+bc+-ca- = ab +bc+ ca =1

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 28#92263Максимум баллов за задание: 7

Дан куб со стороной 1, основаниями $ABCD, A′B ′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′$ и $DD′$ . На рёбрах $A′B′,B ′B,BC,CD, DD′,D′A′$ отмечены точки $K,L,M,N,O,P$ coответственно. Найдите отношение, в котором плоскость $KMO$ делит объём куба, если известно, что

′ ∠A AK = ∠LAK,∠BAM = ∠NAM, ∠DAO = ∠PAO

и что

′ ′ 5 A K+ LB = BM + ND = DO +PA = 4.

Источники: ДВИ - 2024, вариант 244, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В условии нам дана сумма некоторых пар отрезков, быть может, тогда обозначим A’K за x и посчитаем остальные отрезки в грани ABB’A’? Также обратим внимание на то, что ребра в этой грани параллельны, так что можно использовать и подобие!

Подсказка 2

BL = 5/4 - x, LB’ = x - 1/4, а если провести AL до пересечения с A’B’ в точке T, то несложно выразить и B’T. А в составе какого отрезка лежит B’T? Давайте выразим его через больший треугольник!

Подсказка 3

B’T = A’T - 1, а A’T можно выразить через тангенс угла A! Теперь мы умеем выражать B’T двумя способами, чему тогда равен х?

Подсказка 4

x = 1/2! Супер, теперь мы знаем, что K — середина A’B’. Но ведь это верно не только для точки K…

Подсказка 5

Аналогично M — середина BC, O — середина DD’! Теперь мы видим, что сечение у нас достаточно красивое и даже симметричное ;) осталось понять, относительно чего…

Показать ответ и решение

Рассмотрим грань $AA ′B ′B$ . Пусть $A ′K = x,$ тогда $BL = 5− x, 4$ $LB′ = x− 1. 4$

$PIC$

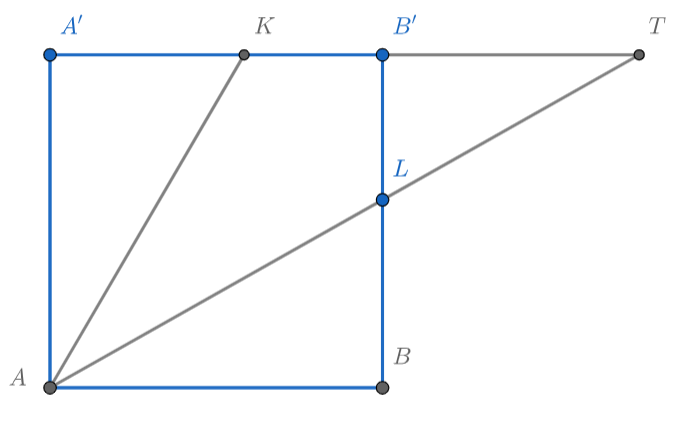
Продлим до пересечения лучи $AL$ и $A′K,$ точку пересечения назовём $T$ и выразим $B′T$ , используя подобие треугольников $ALB$ и $TLB ′ :$

B′T = x-− 14-= 4x−-1. 54 − x 5− 4x

Выразим теперь $′ B T$ вторым способом: через треугольник $′ AA T$ и тангенс $∠A :$

A′K tg∠A′AK = AA′-=x.

Используя формулу тангенса двойного угла, получаем, что

A′T = tg∠A ′AT = -2x-2. 1− x

Отсюда

′ ′ 2x−-1+-x2- 4x−-1 B T = A T − 1= 1− x2 = 5− 4x .

Отсюда можно найти $x$ : перемножая пропорцию и приводя подобные, получим квадратное уравнение $2 4x − 10x+ 4= 0$ , которое имеет решения $x =2$ и $1 x =2.$ По построению $x$ не может превосходить единицу, поэтому $1 x= 2,$ то есть $K$ — середина $′ ′ A B$ .

Аналогично получаем, что $M$ — середина $BC,$ и $O$ — середина $DD ′.$

$PIC$

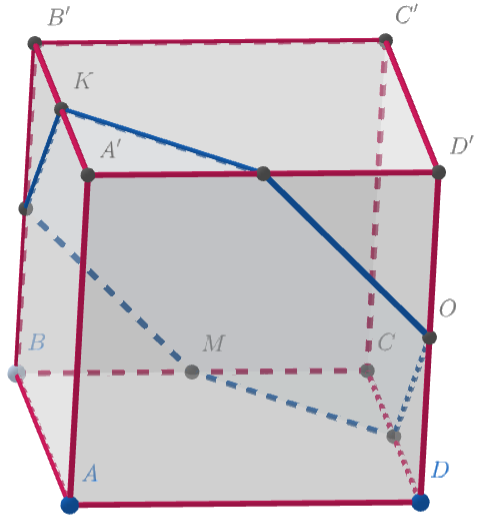
Заметим, что через $K,M,O$ проходит плоскость, которая высекает из данного куба шестиугольник и пересекает ещё три ребра в серединах: рёбра $A ′D ′,BB′$ и $CD$ . Такая плоскость часто встречается в задачах: явно построить сечение можно классическим способом, параллельными переносами отрезков. А если уже встречались с таким построением, можно показать, что все 6 точек действительно лежат в одной плоскости, используя параллельность диагоналям граней куба. Поскольку через три точки $K,M,O$ можно провести только одну плоскость, этот шестиугольник и будет сечением куба плоскостью $KMO.$

Сечение центрально симметрично относительно центра куба $I.$ Середины отрезков $CD$ и $B ′A′$ симметричны относительно центра, как и середины отрезков $A′D′$ и $BC,$ $DD ′$ и $B′B$ . Таким образом, имеем центральную симметрию всего построения относительно центра куба, следовательно, плоскость делит куб на две равные фигуры.

Ответ: 1 : 1

Ошибка.
Попробуйте повторить позже

Задача 29#92341Максимум баллов за задание: 7

Найдите наименьшее целое число, превосходящее число

(16)cos(π∕3) ( 9 )− sin(π∕6) 25 + 25 .

Источники: ДВИ - 2024, вариант 245, задача 1 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Обратите внимание на то, что синус и косинус из условия — это табличные значения! Давайте посчитаем их ;)

Показать ответ и решение

Так как $cos(π∕3) = 1, 2$ а $− sin(π∕6)= − 1, 2$ то получаем

( )12 ( )− 12 1265 + 295 = 45 + 53 = 3175 = 2+ 715

Наименьшее целое число, большее $2+ 715,$ это 3.

Ответ: 3

Ошибка.
Попробуйте повторить позже

Задача 30#92343Максимум баллов за задание: 7

Числа $a ,a,...,a 1 2 20$ образуют арифметическую прогрессию. Найти её разность, если известно, что

2 2 2 a1+a3+ ⋅⋅⋅+ a19 =1330,

2 2 2 a2+ a4+⋅⋅⋅+a20 = 1540

и $a10+a11 = 21.$

Источники: ДВИ - 2024, вариант 245, задача 2 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Нам дана арифметическая прогрессия, так что обозначим ее разность за d. Как можно записать уравнение на сумму из условия через d и один из членов прогрессии?

Подсказка 2

2a₁+ 19d = 21. Теперь подумаем, а как удобнее всего воспользоваться суммой квадратов членов. Интересно, что член с чётным индексом — это соответствующий член с нечетным индексам, увеличенный на d.

Подсказка 3

Отнимите от второго уравнения первое и рассмотрите разность соответствующих квадратов!

Показать ответ и решение

Обозначим разность прогрессии за $d.$ Тогда по условию

a10+ a11 = a1 +9d+ a1+10d= 2a1+ 19d= 21.

Выразим теперь разность сумм квадратов членов с чётными и нечётными индексами.

a2− a2= d2+ 2a d,...,a2 − a2 = d2+2a d. 2 1 1 20 19 19

Складывая все 10 этих выражений, получаем

a2+ a2+ ⋅⋅⋅+ a2 − (a2 +a2+ ⋅⋅⋅+ a2)= 10d2+ 2d(a1+ ⋅⋅⋅+ a19)= 2 4 20 1 3 19

= 10d2+10(2a1+ 18d) =10d(d +(21− d))= 210d= 1540 − 1330= 210.

Отсюда $d= 1.$

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 31#92344Максимум баллов за задание: 7

Решите неравенство

-2x-- logx 3− x ≤ 2.

Источники: ДВИ - 2024, вариант 245, задача 3 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Перед нами логарифмическое неравенство, поэтому не забываем про ОДЗ ;) И в аргументе, и в основании логарифма стоят выражения с неизвестной, какой тогда метод решения удобно применить?

Подсказка 2

Примените метод рационализации! Тогда всё выражение слева разобьется на скобки, а справа будет 0, что будет не так сложно решить ;)

Показать ответ и решение

ОДЗ:

(| -2x-> 0 |{ 3−x ⇐⇒ x∈ (0;1)∪(1;3). ||( x≥ 0 x⁄= 1

Применим метод рационализации:

(-2x- 2) (x− 1) 3− x − x ≤ 0

(x− 1)(3− x)(2x+ x3− 3x2)≤ 0

x(x − 1)2(3− x)(x− 2)≤0

x∈ [0;2]∪ [3;+∞ )

Пересекая с ОДЗ, получаем $x∈ (0;1)∪(1;2].$

Ответ:

$(0;1)∪ (1;2]$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 32#92345Максимум баллов за задание: 7

Решите уравнение

1+ √3 cos2x= --2--(cosx +sinx).

Источники: ДВИ - 2024, вариант 245, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Справа у нас в аргументах функций стоит x, тогда слева раскроем косинус двойного угла по формуле! Как можно преобразовать левую часть, чтобы она стала схожа с правой?

Подсказка 2

После того, как раскроем косинус двойного угла, разложим на скобки разность квадратов. Теперь и слева, и справа есть сумма косинуса и синуса. Видим, что нужно разобрать случаи ;)

Подсказка 3

Или сумма синуса и косинуса равна нулю, или же их разность равна (1 + √3)/2. Первое решить не так сложно, а на какой метод решения намекает √3 справа?

Подсказка 4

Решите второй случай с помощью метода дополнительного аргумента!

Показать ответ и решение

По формуле косинуса двойного угла $cos2x= cos2x− sin2x= (cosx+ sinx)(cosx− sinx).$ После подстановки уравнение принимает вид

1+ √3 (cosx+ sinx)(cosx− sinx)= --2--(cosx+ sinx)

Таким образом, $cosx+sinx= 0$ или $√ - cosx − sinx = 1+2-3.$ Первое из этих уравнений эквивалентно $tgx =− 1,$ то есть $x =− π4 + πk,k ∈ℤ.$

Для решения второго уравнения применим метод дополнительного аргумента:

cosx − sin x= √2(cosπ cosx− sinπ sinx)= √2cos(x+ π) 4 4 4

Тогда второе уравнение эквивалентно

- π 1-1- √3-1-- cos(x+ 4)= 2√ 2 + 2 √2

π π π cos(x+ 4 )=cos(3 − 4)

В итоге, объединяя все ответы

⌊ π | x = −4π + πk,k∈ ℤ ⌈ x = −6π + 2πk,k ∈ℤ x = −3 + 2πk,k ∈ℤ

Ответ:

$− π + πk,− π+ 2πk,− π+ 2πk; k∈ ℤ. 4 6 3$

Ошибка.
Попробуйте повторить позже

Задача 33#92346Максимум баллов за задание: 7

Окружность $Ω 1$ с центром $O 1$ и окружность $Ω 2$ с центром $O 2$ пересекаются в точках $A$ и $B,$ причем $∠O AO =120∘. 1 2$ Окружность, описанная около треугольника $O1AO2$ пересекает окружности $Ω1$ и $Ω2$ соответственно в точках $C$ и $D$ (отличных от точки $A$ ). Найдите угол $∠BDC,$ если известно, что $∘ ∠ACB = 15 .$

Источники: ДВИ - 2024, вариант 245, задача 5 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Что можно сказать про треугольники O₁AO₂ и O₁BO₂? Чем они образованы? Также на рисунке есть немало вписанных углов, давайте отметим те, что связаны с известным ACB!

Подсказка 2

Углы AO₁O₂, BO₁O₂ и ACB равны 15°. Было бы удобно, если бы углы O₁O₂B (его мы можем теперь посчитать) и BDC были аналогично равны, но мы не знаем, лежат ли точки O₁, B, D на одной окружности. Докажем это!

Подсказка 3

Введите точку D’ как пересечение O₁B с со второй окружностью и докажите, что O₁AO₂D’ — вписанный четырехугольник! Для этого можно, например, поотмечать и посчитать уголки ;)

Показать ответ и решение

Треугольники $O AO 1 2$ и $O BO 1 2$ равны по трем сторонам, поэтому $∠AO O = ∠BO O . 1 2 1 2$ Угол $AO B 1$ опирается на дугу $AB$ и является центральным, поэтому оба угла $AO1O2$ и $BO1O2$ равны половине дуги $AB,$ как и опирающийся на нее вписанный угол $ACB.$ Таким образом, $∘ ∠AO1O2 =∠BO1O2 = ∠ACB = 15 .$ Тогда из треугольника $AO1O2$ получаем $∘ ∠AO2O1 = 45.$

$PIC$

Докажем, что точки $C,B$ и $O2$ лежат на одной прямой. Для этого введем точку $C′,$ получающуюся пересечением окружности $Ω1$ и прямой $O2B$ и точку $T,$ получающуся пересечением окружности $Ω2$ и прямой $O2B.$ Докажем, что $C = C′.$ Для этого докажем, что $C ′O1AO2$ — вписанный четырехугольник.

Так как $△O1AO2 = △O1BO2,$ то $∠AO2O1 = ∠BO2O1.$ Угол $AT B$ вписан, поэтому равен половине дуги $AB,$ откуда $∠AT B = ∠AO2O1.$ Треугольник $ATO2$ равнобедренный, поэтому $∠T AO2 = ∠ATO2.$ Рассмотрим треугольники $△ATC ′$ и $△O1AO2.$ В них $∠AO1O2 = ∠AC ′T$ (доказательство аналогично тому, что приведено выше для угла $ACB$ ), $∠AT B = ∠AO2O1.$ Тогда и $∠O1AO2 = ∠C′AT.$ Вычитая из этих углов общую часть — $∠C ′AO2,$ получаем $∠O1AC ′ =∠O2AT.$ Треугольник $AO1C′$ равнобедренный, значит, $∠O1AC ′ =∠O1C ′A.$ Тогда получается, что в описанной окружности треугольника $O1AO2$ углы $O1O2C$ и $BDC$ вписаны и опираются на одну дугу, поэтому равны, причём $∠AO2O1 = ∠BO2O1 =45∘.$

$PIC$

∠O1C′O2+ ∠O1AO2 =(∠O1C′A+ ∠AC ′O2)+ ∠O1AO2 =(∠AO2O1 +∠AO1O2 )+∠O1AO2 = 180∘

Таким образом, $′ O1AO2C$ — вписанный четырёхугольник, то есть описанная окружность треугольника $O1AO2$ пересекает $Ω1$ в точке $C′ = C,$ поэтому $C,B,O2$ — одна прямая. Аналогично можно доказать, что $D,B,O1$ — одна прямая. В итоге $∠BDC =45∘.$

Ответ:

$45∘$

Ошибка.
Попробуйте повторить позже

Задача 34#92347Максимум баллов за задание: 7

Числа $a,b,c,d$ положительны и удовлетворяют соотношению $a+b+ c+ d= 1.$ Найдите наименьшее возможное значение выражения

a2 b2 c2 d2 1− a-+ 1−-b + 1− c-+ 1− d

Источники: ДВИ - 2024, вариант 245, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Рассматривать сумму дробей, у которых в знаменателе стоит разность, не очень удобно. Давайте тогда сделаем замену!

Подсказка 2

Делаем замену 1-a=x, 1-b=y, 1-c=z, 1-d=w. Что тогда можно сказать про их сумму? А как преобразятся дроби, если мы выделим в них целую часть?

Подсказка 3

x+y+z+w=3, а сумма дробей преобразится в выражение с 1/x+1/y+1/z+1/w. Нужно вспомнить, а в каком известном неравенстве есть похожее выражение?

Подсказка 4

Воспользуйтесь неравенством между средним гармоническим и средним арифметическим!

Показать ответ и решение

Первое решение.

Пусть $1− a =x,$ $1− b= y,$ $1− c=z,$ $1− d= w.$ Тогда $x +y+ z+ w= 3,$ и каждое из чисел $x,y,z,w$ положительно. Подставим замену в исходное выражение

a2 b2 c2 d2 (1− x)2 (1− y)2 (1− z)2 (1 − w)2 1−-a + 1−-b + 1−-c + 1−-d =-x- + --y---+ --z---+ --w----

Раскроем скобки в каждом числителе и разделим почленно, тогда получится следующее:

1+ 1 + 1 + 1+ (x+ y+z +w)− 4⋅2= 1 + 1+ 1+ 1-− 5 x y z w x y z w

По неравенству между средним гармоническим и средним арифметическим:

4 1x + 1y + 1z + 1w x+-y+-z+w-≤ -----4------

Таким образом, $1x + 1y + 1z + 1w − 5≥ 136− 5= 13.$ Равенство достигается при $x = y = z = w= 14.$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Заметим, что функция $f(x)= x1−x-$ выпукла на промежутке $(0;1)$ , так как

′ ---1-- f (x) =(x− 1)2

2 f′′(x)= (1-− x)3

Ясно, что при $0 <x <1$ $f′′(x)> 0.$ Так как $a,b,c,d> 0$ и $a+b +c+ d= 1,$ то все эти числа принадлежат промежутку $(0;1).$ Тогда по неравенству Йенсена для функции $f(x)= 1x−x$ получаем

-a2- +-b2-+ -c2-+ -d2- ≥--a2+-b2+-c2+-d2-- 1− a 1 − b 1− c 1− d 1 − (a2+b2+ c2+d2)

Оценим снизу $2 2 2 2 a + b + c+ d :$ по неравенству Коши-Буняковского-Шварца $√ √ -2--2---2--2- a+ b+ c+d ≤ 4 a +b + c +d ,$ откуда $2 2 2 2 1 a + b +c + d ≥ 4.$ Подставим оценку в последнее полученное выражение:

2 2 2 2 1 1-a− (+a2b+b+2+c+c2d+d2) ≥ 1−41 = 13 4

Равенство достигается при $a= b= c= d= 1. 4$

______________________________________________________________________________________________________________________________________________________

Замечание.

Если знать неравенство Седракяна (так же известное, как неравенство Коши-Буняковского-Шварца для дробей)

2 2 a1-+ a2-+...+ a2n-≥ (a1-+a2+-...+-an)2, b1 b2 bn b1+ b2 +...+ bn

то сразу же получаем

-a2-- -b2-- -c2-- -d2-- -----a-+b+-c+d------- 1 1− a + 1− b + 1− c + 1− d ≥ 1− a+1 − b+ 1− c+1− d = 3

Ответ:

$1 3$

Ошибка.
Попробуйте повторить позже

Задача 35#92348Максимум баллов за задание: 7

Все рёбра прямой треугольной призмы $ABCA ′B ′C′$ с основанием $ABC$ и боковыми ребрами $AA ′,$ $BB ′,$ $CC ′$ равны. Найдите отношение, в котором делит объем этой призмы плоскость, проходящая через вершину $′ C$ и через середины ребер $AB,$ $′ AA .$

Источники: ДВИ - 2024, вариант 245, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть M и N — середины AA’ и BB’ соответственно, секущая плоскость пересекает CB в точке K, а T — пересечение KN и TC’. Нам было бы очень полезно узнать, в каком соотношении K делит CB. Давайте тогда попробуем записать какие-нибудь подобия и отношения отрезков!
----—

Подсказка 2

Треугольники CC’T и AMT подобны, так что несложно посчитать CT/AT. А какой теоремой можно воспользоваться для поиска CK/KB?

Подсказка 3

Воспользуемся теоремой Менелая для треугольника ABC и KN! Давайте теперь попробуем начать считать объемы. Пусть V — объем нашей призмы. Как можно посчитать его через имеющиеся на рисунке отрезки?

Подсказка 4

V = 1/2 * AH * BC * BB’. А объемы каких еще фигур можно посчитать через эти же отрезки или V?

Подсказка 5

Выразим через V объемы пирамид ABCC’ и CC’KT! Но ведь для поиска нужного отношения нам не нужен объем кусочка MNTA…значит, нужно его также выразить через V и вычесть! Дело остаётся за малым ;)

Показать ответ и решение

Пусть $M$ и $N$ — середины $AA′$ и $BB′$ соответственно. Пусть секущая плоскость пересекает отрезок $BC$ в точке $K$ и $′ C M ∩ KN = T$ (тогда наше сечение — это $′ KC MN$ ). Ясно, что $T$ лежит на прямой $AC.$ Пусть $AH$ — высота треугольника $ABC.$ Пусть $′ TH ⊥ BC,$ причем $′ H$ лежит на прямой $BC.$

$PIC$

$CC′$ и $AM$ параллельны, причем $AM = 12AA′ = 12CC ′,$ тогда треугольники $CC ′T$ и $AMT$ подобны с коэффициентом $2.$ Тогда $CT = 2AT.$ Треугольники $CAH$ и $TCH ′$ подобны с коэффициентом $2,$ так как $AH || TH ′$ и $TC = 2AC.$ Тогда $TH ′ =2AH.$ По теореме Менелая для треугольника $ABC$ и прямой $KN$ получаем

CK- ⋅ BN-⋅ AT-= 1 KB NA CT

Тогда получаем $CK-= 2, KB 1$ следовательно, $KB-= 1. BC 3$ Пусть $V =V ′′ ′. ABCA B C$ По формуле объема

′ 1 ′ V =SABCBB = 2AH ⋅BC ⋅BB

1 ′ 1 ′ 1 VABCC′ =3CC ⋅SABC = 6CC ⋅AH ⋅BC =3V

VCC′KT = VCC-′KT-⋅ V-= VCC′KT-V-= 4 V V∕3 3 VC′CBA 3 9

V = SANT-⋅ MA ⋅ V-= VAN-⋅AT-⋅sin∠NAT MNTA SABC AA′ 3 6CB ⋅CA ⋅sin∠CAB

Так как $∘ ∠CAB + ∠NAT = 180,$ то $sin∠CAB = sin∠NAT.$ Тогда $-V VMNTA = 12.$

Выразим объем фигуры $′ MC ANKC$ — одной из частей, на которые разделила призму секущая плоскость:

4 1 13 VMC ′ANKC =VCC′KT − VMNTA = 9V − 12V =36V

Тогда $VBKNA ′B′C′ = V − VMC ′ANKC = 2336V.$ Тогда получаем

23 VBKNA′B′C-′= 36V-= 23- VMC ′ANKC 1336V 13

Ответ: 13 : 23

Ошибка.
Попробуйте повторить позже

Задача 36#92361Максимум баллов за задание: 7

Найдите наименьшее целое число, превосходящее число

√- √- log2(3+ 2 2)− log2(1+ 2).

Источники: ДВИ - 2024, вариант 246, задача 1 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Внимательно посмотрим на наше выражение. Может быть, есть какое-то свойство, которое прямо напрашивается, чтобы его применили?

Подсказка 2

Да, действительно, применить формулу для разности логарифмов с одинаковым основанием — это отличная идея! В новом аргументе теперь как-то слишком много выражений с корнями, стоит как-то его упростить. Что для этого можно сделать?

Подсказка 3

Умножение на сопряжённое — лучший выбор. Давайте избавимся от корня в знаменателе.

Подсказка 4

Осталось только оценить аргумент относительно ближайших известных нам значений, при равенстве аргумента логарифма которым, получатся целые значения, и найти ответ.

Показать ответ и решение

По свойствам логарифмов

√ - √ - ( 3+ 2√2 ) log2(3+2 2)− log2(1 + 2) =log2 1+-√2- =

Домножаем на сопряжённое, чтобы применить формулу разности квадратов

((3+ 2√2-)(√2− 1)) ( √-) = log2 -(1+-√2)(√2-−-1)- = log2 1+ 2

Так как $√- 1< 2 <2,$ то $√ - 2 <1 + 2<3 <4.$ Тогда получаем, что

1= log2(2)< log2(1+ √2)< log2(4)= 2.

Таким образом, искомое число это $2.$

Ответ: 2

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 37#92362Максимум баллов за задание: 7

Найдите количество всех упорядоченных четвёрок чисел $a,b,c,d$ , таких что числа

2 2 2 2 2 2 a − ab +b ,b − bc +c ,c − cd+d

равны друг другу, если известно, что каждое из чисел $a,b,c,d$ равно либо 1, либо 2, либо 3, а число $a$ является среди них максимальным.

Источники: ДВИ - 2024, вариант 246, задача 2 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Если есть равные выражения, то что стоит попробовать сделать в первую очередь?

Подсказка 2

Да, приравниваем и смотрим, что получится. Например первое со вторым и второе с третьим. Если у нас есть некоторое равенство, то к какому виду стоит его привести, чтобы в дальнейшем было проще с ним работать?

Подсказка 3

Как и в самых обычных уравнениях — перенесем все влево, оставив справа 0, и попробуем разложить на множители.

Подсказка 4

Получили два произведения, равные нулю, то есть хотя бы один множитель из одного произведения и хотя бы один множитель из второго равны нулю, значит, нужно рассмотреть все возможные случаи, банально их перебрав.

Подсказка 5

Не забудьте, что а по условию — наибольшее число, и в ответ просят указать именно количество упорядоченных четвёрок, а не сами четвёрки.

Показать ответ и решение

Замечание. В оригинальном условии на экзамене была опечатка, которая делала задачу некорректной. Решение приведено для нового условия, которое дано на сайте.

_________________________________________________________________________________________________________________________________________________________________________________

Условие о равенстве трех чисел эквивалентно выполнению следующей системы:

{ 2 2 2 2 a2− ab+ b2 =b2− bc+ c2 b − bc+c = c − cd+ d

Переносим в каждом уравнении правую часть влево и раскладываем на множители:

{ (a− c)(a+ c− b)= 0 (b− d)(b+d − c)= 0

Тогда возможны $4$ случая:

1.: $a =c$ и $b= d.$ В этом случае, если $a =3,$ то остается выбрать значение $b= 1,2,3$ ( $3$ способа), если $a =2,$ то $b=1,2$ ( $2$ способа) и $a= 1,$ $b =1$ ( $1$ способ), то есть всего $6$ способов;
2.: $a =c$ и $b+ d− c =0.$ В этом случае имеем $b+ d= c.$ Тогда $b+ d≥ 2,$ поэтому $c≥ 2.$ С другой стороны, $c≤ 3,$ поэтому $b+ d≤ 3.$ Тогда $b+d =2$ или $3$ и $a$ и $c$ равны $2$ или $3.$ Если $b+d =2,$ то $b=d =1,$ и $a= c,$ и этот случай мы учли выше. Если же $b+d =3,$ то тут всего два случая: $a =c= 3$ и $b= 1,$ $d =2$ или $b= 2,$ $d =1.$ Таким образом, имеем $2$ варианта;
3.: $a +c− b= 0$ и $b= d.$ Этот случай симметричен предыдущему, но в нем возможны только случаи $b= d= 2,$ $a= c= 1$ (который нас не интересует, так как $a$ — наибольшее число) и $b= d= 3$ и $a+ c= 3,$ в которых $a≤ 2,$ что тоже нас не интересует;
4.: $a +c− b= 0$ и $b+d − c= 0.$ Сложим два этих равенства и получим, что $a+ d= 0,$ что невозможно, поскольку $a≥1,$ $d ≥1.$

Таким образом, получаем $6 +2= 8$ упорядоченных четверок.

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 38#92363Максимум баллов за задание: 7

Решите неравенство

(2 ) ( 2 ) logx− 1(2x− 5)+ log4x2− 20x+25 x − 2x+ 1 − log2x−5 4x − 20x+ 25 ≤0.

Источники: ДВИ - 2024, вариант 246, задача 3 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Сначала выпишем ОДЗ, куда же без неё? Какие ограничения есть у логарифмов?

Подсказка 2

Помимо положительности аргумента и основания, не забываем, что основание не может быть равно ещё и единице. Остается решить систему, и наша ОДЗ готова! Самое время внимательно посмотреть на аргументы и основания: может быть, их можно как-то преобразовать, чтобы получились везде похожие выражения относительно х?

Подсказка 3

ФСУ — наш лучший друг, а с учетом ОДЗ еще и свойства логарифмов должны прекрасно примениться. Если всё максимально упростить и привести подобные, может быть, удастся применить ещё одно свойство логарифмов?

Подсказка 4

Вынесли степени на ОДЗ, все привели и получили два прекрасных логарифма, причем основание первого является аргументом второго и наоборот. Самое время для замены :)

Подсказка 5

Вспомним, что log_a(b)=1/log_b(a). После замены получится простейшее дробно-рациональное неравенство. Останется сделать только обратную замену!

Подсказка 6

Не забудьте, что знак нестрогий — есть вероятность, что вы что-то потеряли в ответе ;)

Показать ответ и решение

Сначала запишем ОДЗ:

( x − 1⁄= 1 ||||| ||||| x −2 1> 0 |{ 4x2− 20x +25⁄= 1 ||| 4x − 20x +25> 0 ||||| 2x− 5⁄= 1 |||( 2x2− 5> 0 x − 2x+ 1> 0

Так как $x2− 2x+ 1= (x− 1)2,$ $4x2− 20x +25= (2x− 5)2,$ то получаем, что система, указанная выше, эквивалентна следующей:

( x⁄= 2 ||||| |{ x> 1 ||| 2x− 5 ⁄=− 1 |||( x⁄= 35 x> 2

Из третьего неравенства получаем, что $x ⁄=2.$ Тогда, пересекая все неравенства, получаем $x∈ (2,5;3)∪(3;+ ∞).$

Теперь преобразуем исходное неравенство:

( 2) ( 2) logx−1(2x− 5)+ log(2x−5)2 (x− 1) − log2x−5 (2x− 5) ≤ 0

С учетом ОДЗ и свойств логарифма получаем:

logx−1(2x− 5)+ log2x−5(x− 1)− 2log2x−5(2x − 5)≤ 0

logx−1(2x − 5)+ log2x−5(x− 1)− 2≤ 0

Пусть $logx−1(2x− 5)= t.$ Тогда уравнение принимает вид:

t+ 1− 2≤0 t

Приводим к общему знаменателю:

t2−-2t+-1≤ 0 t

(t−-1)2 t ≤ 0

Решив данное неравенство, получаем $t< 0$ или $t= 1.$ Из $t= 1$ получаем $logx−1(2x− 5)= 1,$ откуда $x= 4.$ Теперь сделаем обратную замену для $t<0$ :

logx−1(2x− 5)<0

По методу рационализации:

(x − 2)(2x− 6)< 0

Решаем неравенство и получаем, что $x∈ (2;3).$ Пересекая с ОДЗ, получаем $x∈ (2,5;3).$

Ответ:

$(2,5;3)∪ {4}$

Ошибка.
Попробуйте повторить позже

Задача 39#92364Максимум баллов за задание: 7

Решите уравнение

√- tgx − 4sin x= 3.

Источники: ДВИ - 2024, вариант 246, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Посмотрим внимательно на наше уравнение: формулы, которую можно удачно применить, сходу не видно – что будем делать? Возможно, стоит поработать с тангенсом?

Подсказка 2

Итак, видим тангенс – пишем ограничение. Может быть сразу перепишем его по определению как sin(x)/cos(x)?

Подсказка 3

Что хочется сделать, когда видим дробь? Удобно ли тут привести её к общему знаменателю? А может быть удастся вообще избавиться от него?

Подсказка 4

Не напоминает ли какое-то из слагаемых формулу для двойного угла? Перенесите его в правую часть и попробуйте преобразовать всё что осталось слева.

Подсказка 5

Удачное применение формулы для вспомогательного угла поможет свести уравнение к виду sin(a) = sin(b) – а уж такое решать мы умеем!

Показать ответ и решение

ОДЗ этого уравнения состоит из единственного условия: $cosx⁄= 0,$ что эквивалентно $x ⁄= π+ πd,d∈ ℤ. 2$ Далее умножаем уравнение на $cosx,$ тогда оно принимает вид:

√ - sinx − 4sinx cosx= 3cosx

Используем формулу двойного аргумента и переносим правую часть влево:

√ - (sinx − 3cosx)− 2sin2x= 0

Разделим уравнение на $2$ и воспользуемся методом дополнительного аргумента:

sin(x − π )=sin 2x 3

[ x − π− 2x = 2πk,k∈ ℤ x − 3π+ 2x = π+ 2πk ∈ℤ 3

[ x =− π3 − 2πk,k ∈ℤ x = 4π9-+ 2πk3 ,k∈ ℤ

Ответ:

$− π + 2πk,4π + 2πk; k∈ ℤ 3 9 3$

Ошибка.
Попробуйте повторить позже

Задача 40#92365Максимум баллов за задание: 7

В треугольнике $ABC$ угол $A$ является тупым. На стороне $BC$ отмечена точка $D$ таким образом, что $AC = CD$ . При этом окружность, описанная около треугольника $ACD$ , касается прямой $AB$ в точке $A.$ На прямой $AD$ отмечена точка $E$ таким образом, что $CE = EA = AB.$ Найдите отношение $BC :AB.$

Источники: ДВИ - 2024, вариант 246, задача 5 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Нарисуем чертёж и подумаем – откуда могло бы взяться искомое отношение? Длины сторон нам неизвестны, на равнобедренный треугольник не похож, что остаётся делать?

Подсказка 2

Будем думать про углы и искать подобия! Как можно в этом контексте использовать условие об окружности и касательной?

Подсказка 3

Вспоминаем теорему об угле между касательной и хордой! Теперь у нас появилась пара равнобедренных треугольников, у которых равны углы при вершине – какой вывод можно сделать?

Подсказка 4

Выходит, треугольники EAB и ACD подобны! Отметьте в них равные углы и сделайте вывод о четырёхугольнике ABEC.

Подсказка 5

Осталось поработать с отношениями в подобных треугольниках и свойствами параллелограмма, после чего задача будет побеждена!

Показать ответ и решение

$PIC$

По свойству угла между касательной и хордой $∠EAB = ∠ACD.$ А учитывая, что треугольники $EAB$ и $ACD$ равнобедренные, можем сказать, что они подобны. Значит, $∠AEB = ∠CAD,$ а т.к. треугольник $ACE$ равнобедренный, то $∠ACE =∠CAD = ∠AEB.$ Следовательно, $∠AEC =∠EAB,$ из этого получаем, что $CE ∥AB,$ а раз $CE = AB,$ то $ABEC$ — параллелограмм.