ДВИ 2011
Ошибка.
Попробуйте повторить позже
В кубе с ребром 1 расположены две сферы различных радиусов. Первая касается плоскости основания и двух соседних боковых граней куба. Вторая сфера касается двух других боковых граней куба, грани куба, параллельной основанию, и первого шара. Чему равна сумма радиусов сфер?
Источники:
Подсказка 1
Давайте сначала вспомним, что мы знаем о сфере, вписанной в некую фигуру. Есть что-то особенное в ее местоположении?
Подсказка 2
Да, центр сферы лежит на биссектрисе трёхгранного угла, в который вписана сфера! Тогда что можно сказать о центрах наших сфер, раз они вписаны в куб?
Подсказка 3
Они лежат на диагонали куба, так как диагональ куба как раз и является биссектрисой соответствующих трёхгранных углов. А кусочек диагонали между центрами как раз и есть сумма радиусов, которую нам нужно найти! Длину чего тогда стоит узнать и какую плоскость тогда имеет смысл рассмотреть?
Подсказка 4
Пусть это будет сечение куба, перпендикулярное основанию и содержащее эту самую диагональ. Раз уж сферы касаются граней куба, то что имеет смысл отметить дополнительно?
Подсказка 5
Радиусы, проведенные в точки касания окружностей и оснований, тоже будут лежать в этой плоскости сечения. Может быть, в таком случае выйдет как-то выразить оставшиеся кусочки диагонали тоже через радиусы окружностей?
Подсказка 6
Зная длину ребра куба, легко можем вычислить длину диагонали куба, а также синус угла между этой диагональю и основанием. А зная синус угла, можно и оставшиеся отрезочки диагонали через радиусы выразить. Осталось только записать их сумму и выразить сумму радиусов!
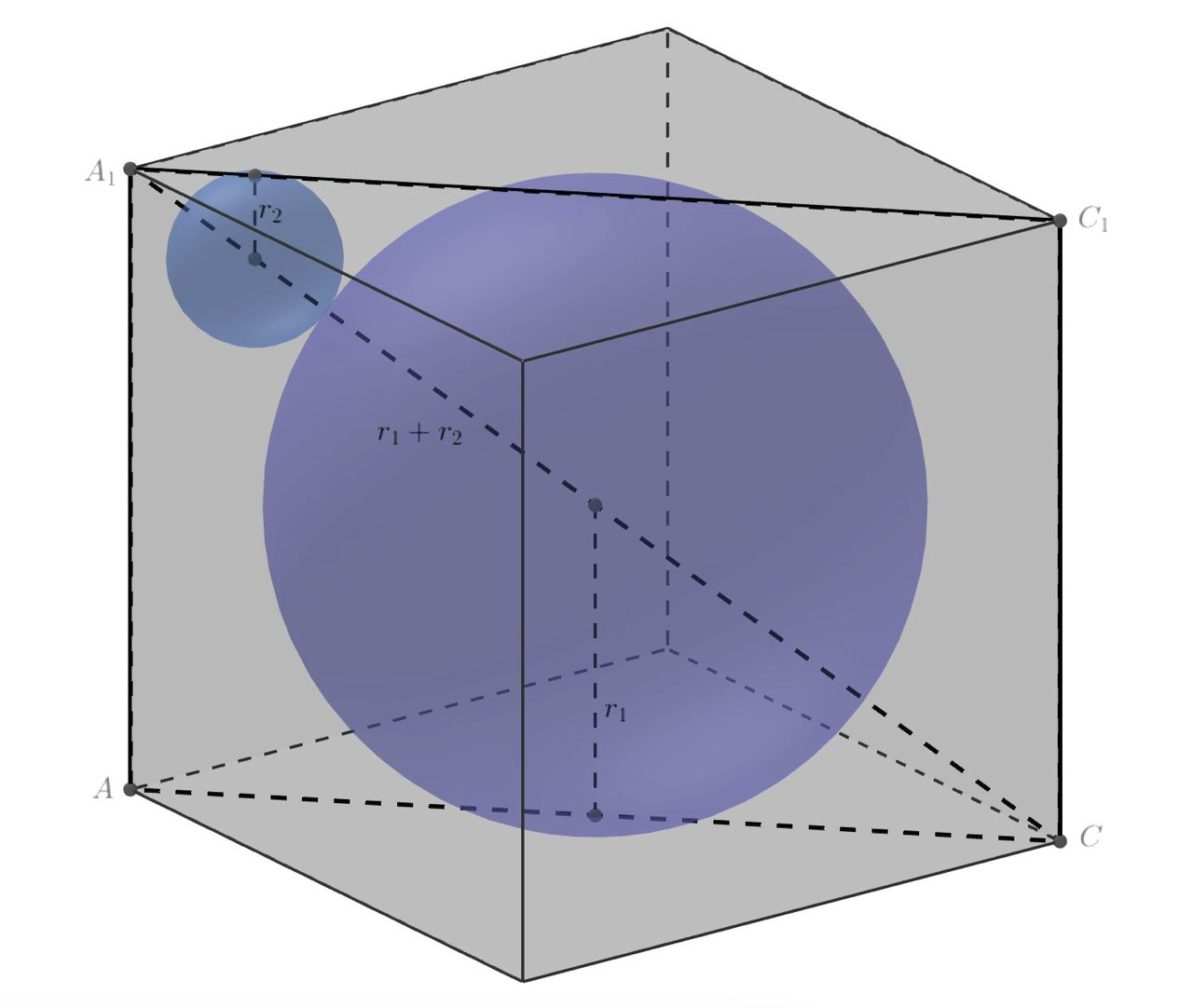
Заметим, что центры обеих сфер лежат на диагонали куба, причём на одной и том же, поскольку касаются разных боковых граней.
Действительно, прямая, на которой лежит центр сферы, является биссектрисой трёхгранного угла, поскольку центр куба является центром
сферы радиуса , которая касается всех граней, то эта прямая проходит через него. Без ограничения общности, выберем на эту роль
диагональ
.
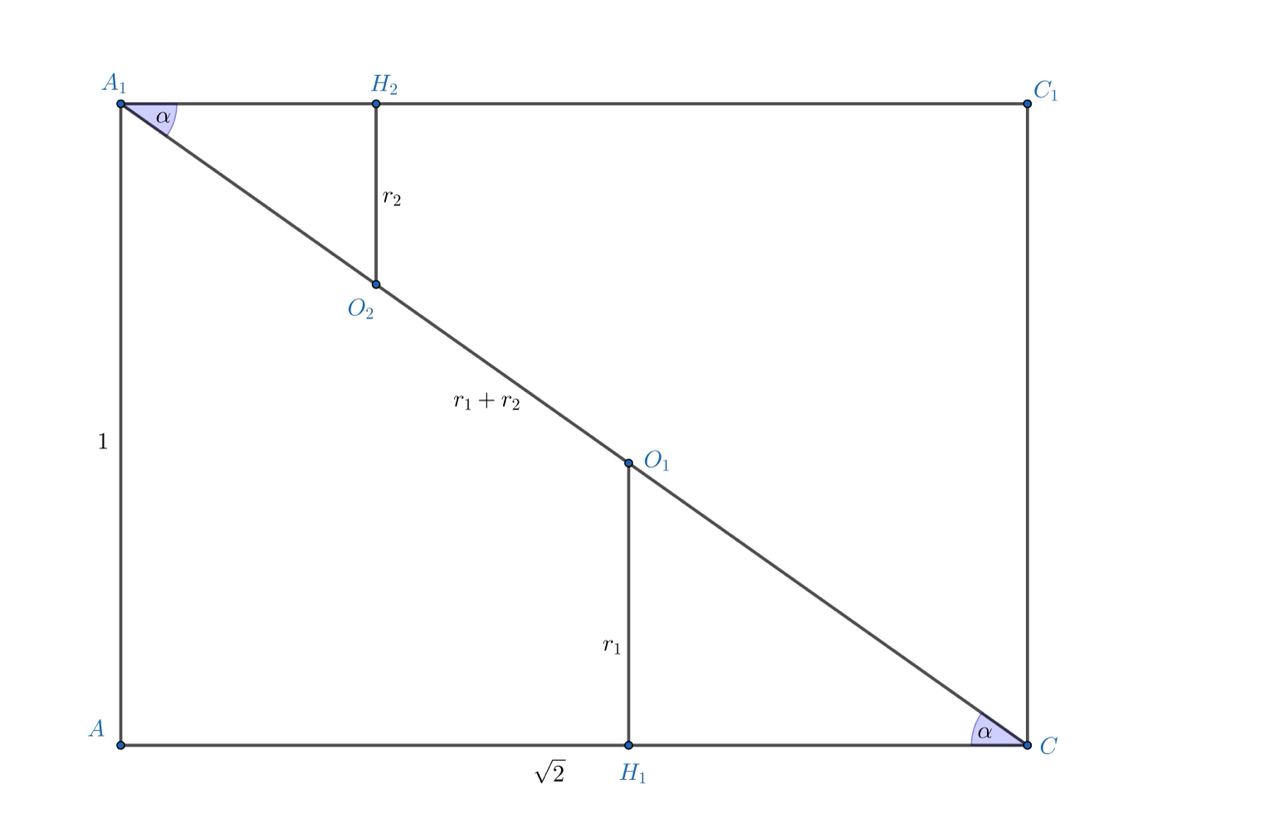
Пусть тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




