№17 из ЕГЭ 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дан ромб На диагонали
отмечены точки
и
так, что
Прямая
пересекает сторону
в точке
а прямая
пересекает сторону
в точке
а) Докажите, что площадь четырехугольника равна площади
треугольника
б) Найдите если известно, что
и около пятиугольника
можно описать окружность.
Источники:
а) Так как — ромб, то
и
Тогда по двум углам:
как накрест
лежащие углы при параллельных прямых,
как вертикальные.
Запишем отношение подобия:
Следовательно, Так как
— ромб, то
то есть
и
— середина
Аналогично по двум углам:
как
накрест лежащие углы при параллельных прямых,
как
вертикальные.
Запишем отношение подобия:
Следовательно, То есть
— середина
Тогда так
как
— ромб, то
Проведем диагональ Обозначим площадь ромба
за
Так как
диагонали ромба разбивают его на два равных треугольника, то
а
также
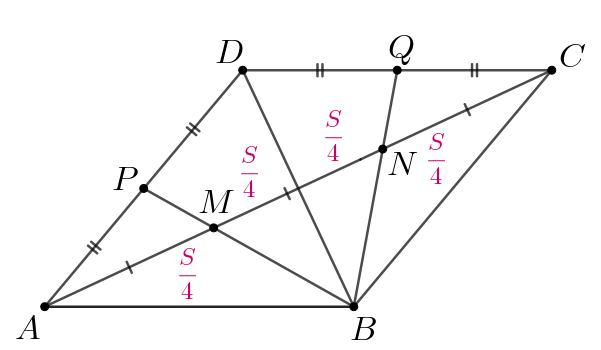
Рассмотрим треугольник и его медиану
Так как медиана
разбивает треугольник на два равновеликих треугольника, то получаем:
Рассмотрим треугольник и его медиану
Тогда аналогично
имеем:
Так как четырехугольник состоит из треугольников
и
то получаем:
б) Проведем и
Так как
и
— середины
и
соответственно, то
— средняя линия треугольника
Отсюда
Аналогично — средняя линия треугольника
то есть
Так как и
то
— трапеция. Трапеция,
вписанная в окружность является равнобедренной, следовательно,
Аналогично — вписанная трапеция, то есть
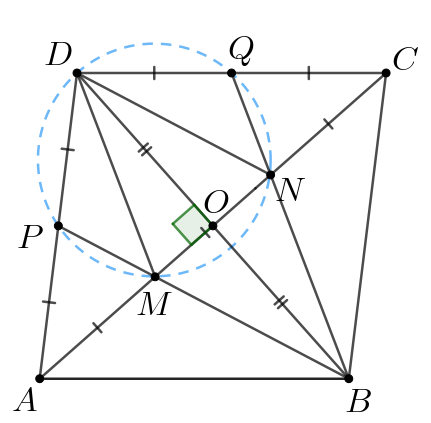
Так как то имеем:
Пусть и
пересекаются в точке
Так как диагонали ромба точкой
пересечения делятся пополам, то получаем:
Также диагонали ромба перпендикулярны, тогда по теореме Пифагора для
прямоугольного треугольника
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан ромб На диагонали
отмечены точки
и
так, что
Прямая
пересекает сторону
в точке
а прямая
пересекает сторону
в точке
а) Докажите, что площадь четырехугольника равна площади
треугольника
б) Найдите если известно, что
и около пятиугольника
можно описать окружность.
Источники:
а) Так как — ромб, то
и
Тогда по двум углам:
как накрест
лежащие углы при параллельных прямых,
как вертикальные.
Запишем отношение подобия:
Следовательно, Так как
— ромб, то
то есть
и
— середина
Аналогично по двум углам:
как
накрест лежащие углы при параллельных прямых,
как
вертикальные.
Запишем отношение подобия:
Следовательно, То есть
— середина
Тогда так
как
— ромб, то
Проведем диагональ Обозначим площадь ромба
за
Так как
диагонали ромба разбивают его на два равных треугольника, то
а
также
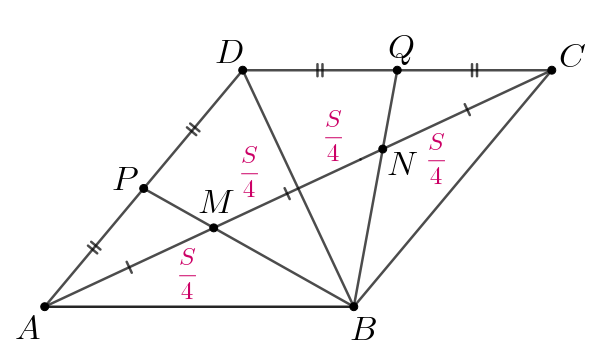
Рассмотрим треугольник и его медиану
Так как медиана
разбивает треугольник на два равновеликих треугольника, то получаем:
Рассмотрим треугольник и его медиану
Тогда аналогично
имеем:
Так как четырехугольник состоит из треугольников
и
то получаем:
б) Проведем и
Так как
и
— середины
и
соответственно, то
— средняя линия треугольника
Отсюда
Аналогично — средняя линия треугольника
то есть
Так как и
то
— трапеция. Трапеция,
вписанная в окружность является равнобедренной, следовательно,
Аналогично — вписанная трапеция, то есть
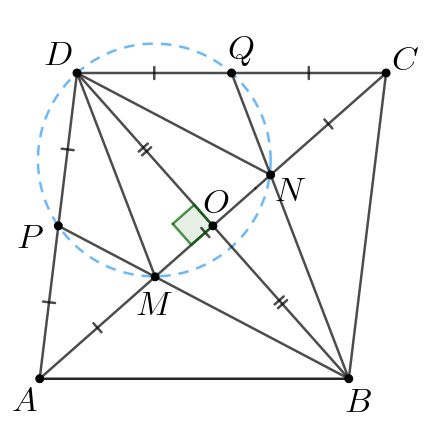
Так как то имеем:
Пусть и
пересекаются в точке
Так как диагонали ромба точкой
пересечения делятся пополам, то получаем:
Также диагонали ромба перпендикулярны, тогда по теореме Пифагора для
прямоугольного треугольника
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан ромб На диагонали
отмечены точки
и
так, что
Прямая
пересекает сторону
в точке
а прямая
пересекает сторону
в точке
а) Докажите, что площадь четырехугольника равна площади
треугольника
б) Найдите если известно, что
и около пятиугольника
можно описать окружность.
Источники:
а) Так как — ромб, то
и
Тогда по двум углам:
как накрест
лежащие углы при параллельных прямых
и
и секущей
как вертикальные.
Запишем отношение подобия:
Следовательно, Так как
— ромб, то
и
то есть
и
— середина
Аналогично по двум углам:
как
накрест лежащие углы при параллельных прямых
и
и секущей
как вертикальные.
Запишем отношение подобия:
Следовательно, То есть
— середина
Тогда так
как
— ромб, то
Проведем диагональ Обозначим площадь ромба
за
Так как
диагонали ромба разбивают его на два равных треугольника, то
а
также
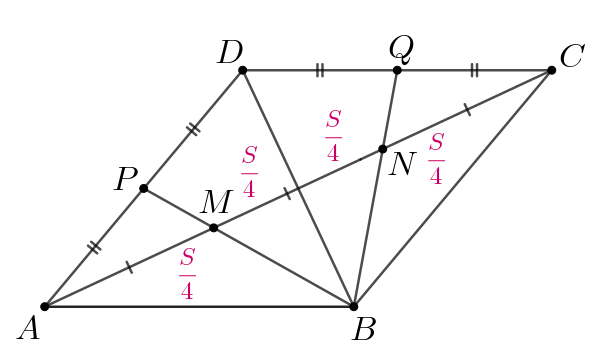
Рассмотрим треугольник и его медиану
Так как медиана
разбивает треугольник на два равновеликих треугольника, то получаем:
Рассмотрим треугольник и его медиану
Тогда аналогично
имеем:
Так как четырехугольник состоит из треугольников
и
то получаем:
б) Проведем и
Так как
и
— середины
и
соответственно, то
— средняя линия треугольника
Отсюда
Аналогично — средняя линия треугольника
то есть
Так как и
то
— трапеция. Трапеция,
вписанная в окружность, является равнобедренной, следовательно,
Аналогично — вписанная трапеция, то есть
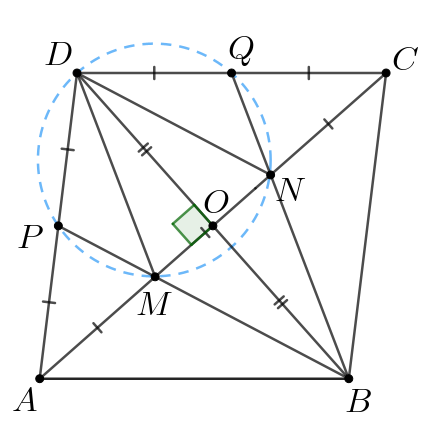
Так как то имеем:
Пусть и
пересекаются в точке
Так как диагонали ромба точкой
пересечения делятся пополам, то получаем:
Также диагонали ромба перпендикулярны, тогда по теореме Пифагора для
прямоугольного треугольника
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан ромб На диагонали
отмечены точки
и
так, что
Прямая
пересекает сторону
в точке
а прямая
пересекает сторону
в точке
а) Докажите, что площадь четырехугольника равна площади
треугольника
б) Найдите если известно, что
и в пятиугольник
можно вписать окружность.
Источники:
а) Так как — ромб, то
и
Тогда по двум углам:
как накрест
лежащие углы при параллельных прямых
и
и секущей
как вертикальные.
Запишем отношение подобия:
Следовательно, Так как
— ромб, то
и
то есть
и
— середина
Аналогично по двум углам:
как
накрест лежащие углы при параллельных прямых
и
и секущей
как вертикальные.
Запишем отношение подобия:
Следовательно, То есть
— середина
Тогда так
как
— ромб, то
Проведем диагональ Обозначим площадь ромба
за
Так как
диагонали ромба разбивают его на два равных треугольника, то
а
также
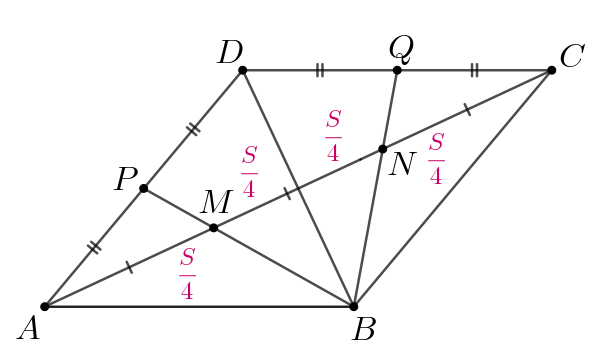
Рассмотрим треугольник и его медиану
Так как медиана
разбивает треугольник на два равновеликих треугольника, то получаем:
Рассмотрим треугольник и его медиану
Тогда аналогично
имеем:
Так как четырехугольник состоит из треугольников
и
то получаем:
б) Пусть стороны ромба равны Тогда
По условию в пятиугольник можно вписать окружность.
Значит, в четырехугольник
вписана та же окружность, так как
точка
— точка пересечения продолжений сторон пятиугольника
и
По свойству вписанной в четырехугольник окружности имеем:
Выразим отрезок и подставим известные значения:
Пусть — точка пересечения диагоналей. Точка пересечения диагоналей
ромба делит диагонали пополам. Значит,
Треугольник прямоугольный, так как диагонали ромба пересекаются
под прямым углом. По теореме Пифагора получаем:
Точка делит диагонали пополам как точка пересечения диагоналей ромба.
Значит,
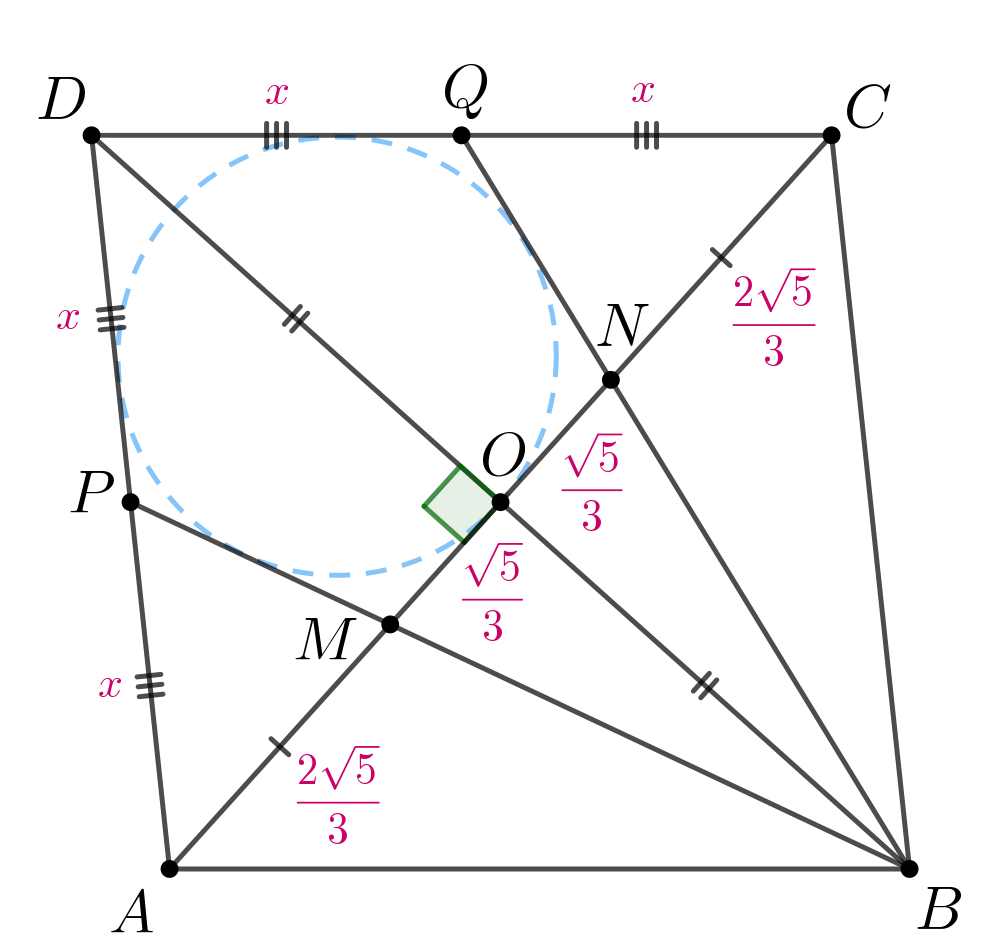
Треугольник прямоугольный, так как диагонали ромба пересекаются
под прямым углом. По теореме Пифагора получаем:
В треугольнике медианы
и
пересекаются в точке
следовательно,
Из этого получаем равенство:
Найдем диагональ
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан ромб Точки
и
— середины сторон
и
соответственно.
Проведены
и
таким образом, что они пересекают диагональ
в
точках
и
соответственно.
а) Докажите, что сумма площадей треугольников и
равна
площади треугольника
б) Известно, что в можно вписать окружность. Найдите радиус этой
окружности, если сторона ромба равна
Источники:
а) Так как — ромб, то диагонали точкой пересечения делятся
пополам.
Пусть — точка пересечения диагоналей, тогда
В треугольнике точка
— точка пересечения медиан, следовательно,
В треугольнике точка
— точка пересечения медиан, следовательно,
Пусть Из того, что
получаем:
Проведем диагональ Обозначим площадь ромба
за
Так как диагональ ромба разбивает его на два равных треугольника, то
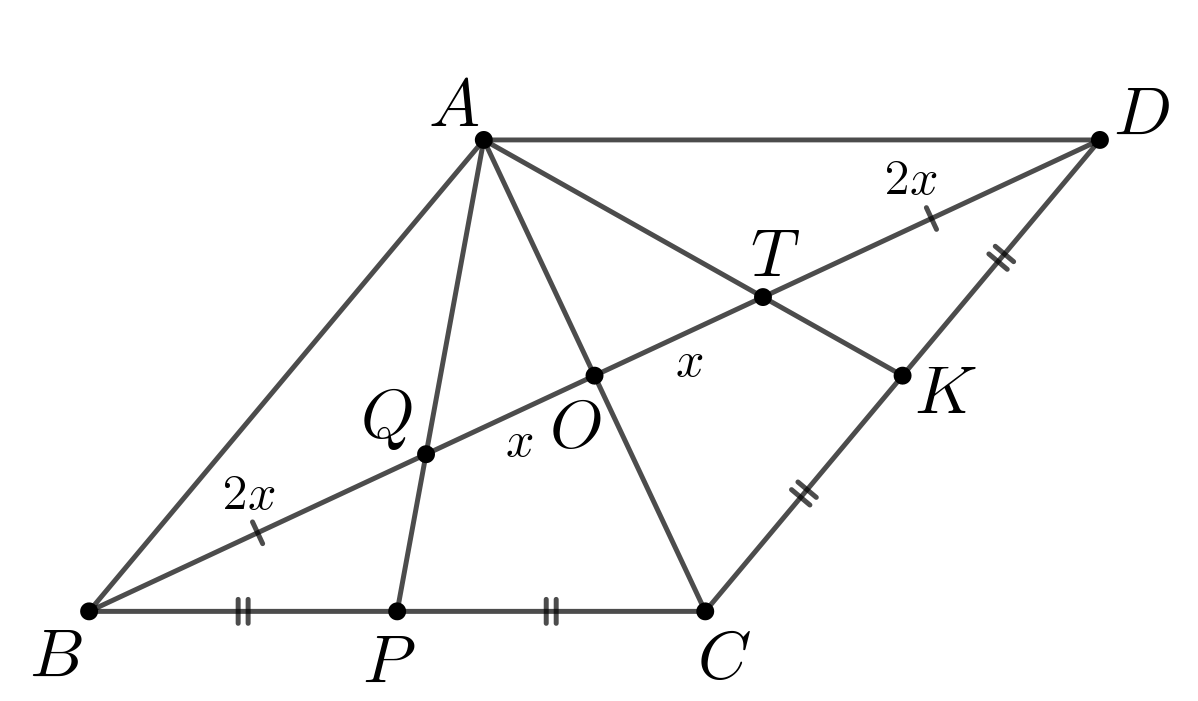
Далее, треугольники
и
имеют общую высоту из
вершины
тогда их площади относятся как длины оснований, к которым
проведена эта высота. Отсюда получаем:
Так как точка — точка пересечения медиан треугольника
то
Аналогично, так как точка — точка пересечения медиан треугольника
то
Кроме того, треугольники и
имеют общую высоту из вершины
а также треугольники
и
имеют общую высоту из вершины
Отсюда получаем:
Из этого следует искомое равенство:
б) По условию в пятиугольник можно вписать окружность. Значит, в
четырехугольник
вписана та же окружность, так как точка
— точка
пересечения продолжений сторон пятиугольника
и
Кроме того, та же
окружность вписана в треугольник
По свойству вписанной в четырехугольник окружности имеем:
Выразим отрезок и подставим известные значения:
Треугольник прямоугольный, так как диагонали ромба пересекаются
под прямым углом. По теореме Пифагора получаем:
Точка делит диагонали пополам, как точка пересечения диагоналей ромба.
Значит,
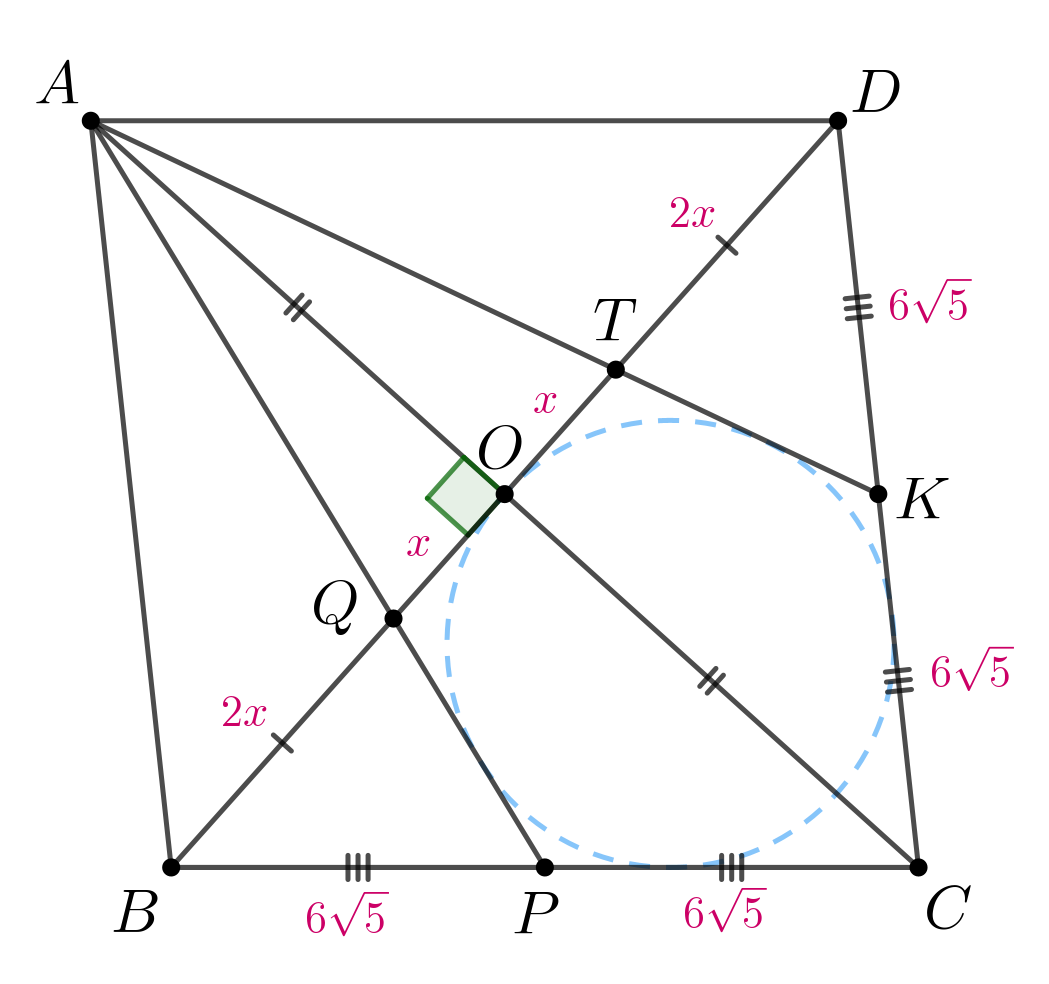
Треугольник прямоугольный, так как диагонали ромба пересекаются
под прямым углом. По теореме Пифагора получаем:
В треугольнике медианы
и
пересекаются в точке
следовательно,
Из этого получаем равенство:
Найдем площадь треугольника
Найдем полупериметр треугольника
Из формулы площади треугольника найдем радиус вписанной
окружности:
б) 8
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В трапеции точка
— середина основания
точка
—
середина боковой стороны
Отрезки
и
пересекаются в точке
a) Докажите, что площади четырёхугольника и треугольника
равны.
б) Найдите отношение площади четырёхугольника к площади
трапеции
если
Источники:
а) Продлим до пересечения с прямой
в точке
Заметим, что
как вертикальные,
как накрест лежащие при
параллельных прямых
и
и секущей
по условию. Тогда
треугольники
и
равны по стороне и двум прилежащим к ней
углам.
В равных треугольниках соответственные элементы равны, в частности,
и
Тогда
— средняя линия треугольника
следовательно,
Значит,
— трапеция.
Треугольники, образованные отрезками диагоналей трапеции и её боковыми сторонами, являются равновеликими, то есть имеют одинаковую площадь.
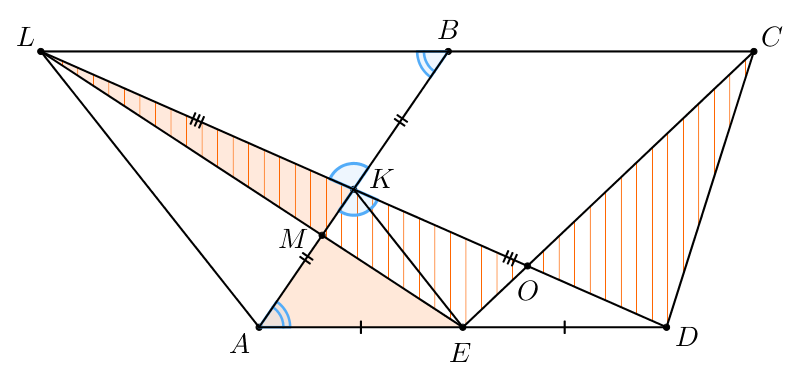
Пусть в трапеции диагонали
и
пересекаются в точке
Тогда
В трапеции диагонали
и
пересекаются в точке
Тогда
Таким образом,
б) В предыдущем пункте мы доказали, что Тогда
найдем отношение площади треугольника
к площади трапеции
Также мы доказали равенство треугольников и
значит, равны и
их площади. Тогда
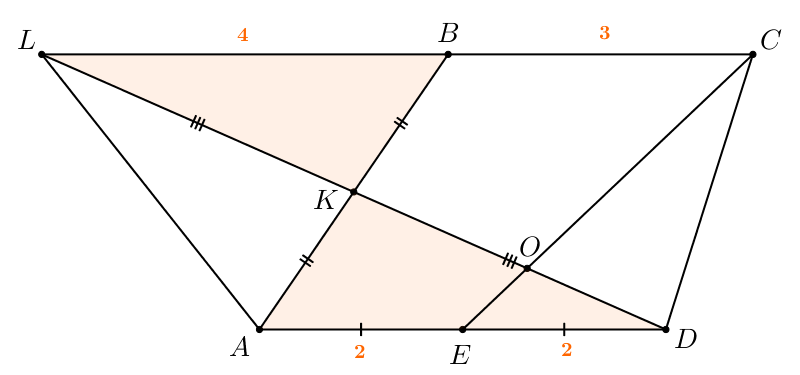
Значит, нам нужно найти отношение площадей треугольников и
Такое отношение равно отношению их сторон
и
Рассмотрим треугольники и
В них
как
вертикальные и
как накрест лежащие, образованные
параллельными прямыми
и
и секущей
Значит,
по двум углам. Запишем отношение подобия:
Тогда Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан прямоугольник Известно, что
Точка
— середина его
стороны
На стороне
отмечена точка
Известно, что
Точка
— середина отрезка
а) Докажите, что точки
и
лежат на одной прямой.
б) Найдите если известно, что
Источники:
а) Продлим до пересечения с прямой
в точке
Пусть
пересекает
в точке
Тогда нам нужно доказать, что
— середина
Заметим, что треугольник подобен треугольнику
по двум углам,
так как
как накрест лежащие при
и секущей
и
Запишем отношение подобия:
Пусть Тогда
и

Тогда по теореме Менелая для треугольника и секущей
имеем:
Следовательно, пересекает отрезок
в его середине, а значит, точка
и есть точка
из условия. Тогда точки
и
лежат на одной
прямой.
б) Если то
Тогда
По теореме Пифагора для треугольника
Значит,

Тогда из прямоугольного треугольника
Рассмотрим треугольник В нем
Тогда по теореме косинусов
Таким образом,
б) 5
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
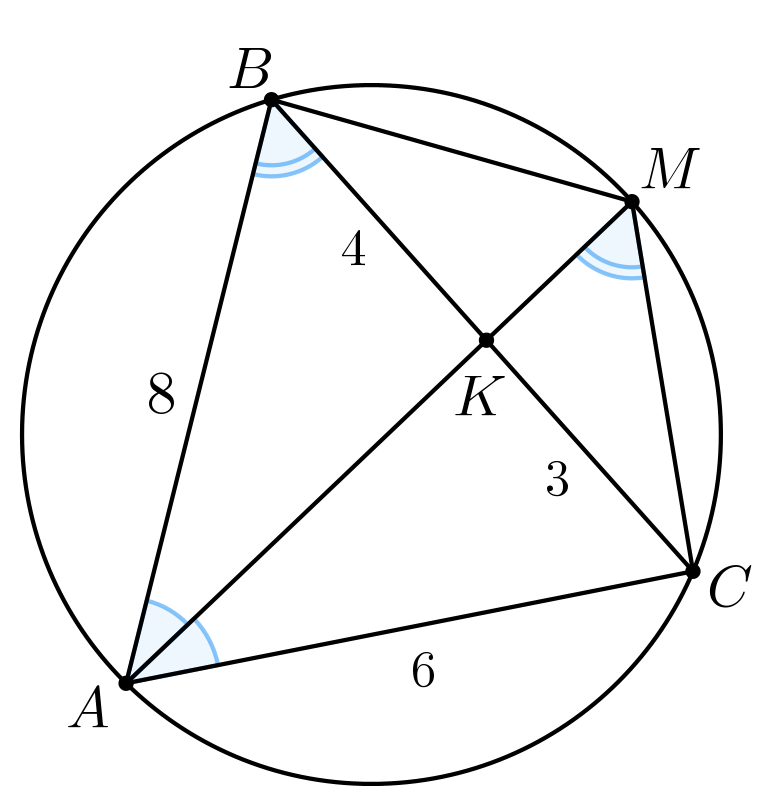
Биссектриса угла треугольника
пересекает его сторону
в точке
и его описанную окружность в точке
а) Докажите, что треугольник – равнобедренный.
б) Найдите радиус окружности, описанной около треугольника если
и
Источники:
а) Углы и
равны, как вписанные углы, опирающиеся на одну дугу
Аналогично углы и
равны, как вписанные углы, опирающиеся
на одну дугу

В треугольнике углы
и
равны, так как
—
биссектриса угла
Таким образом, получаем равенство:
В треугольнике углы
и
равны, следовательно,
треугольник
— равнобедренный с основанием
б) Запишем для треугольника теорему косинусов:
Выразим косинус угла и подставим известные значения:
Из основного тригонометрического тождества:
Углы и
равны, как вписанные углы, опирающиеся на одну дугу
значит и их синусы также равны.
Биссектриса угла делит противолежащую сторону на отрезки, пропорциональные
прилежащим сторонам. По свойству биссектрис для треугольника
Из того, что следует, что
Запишем для треугольника теорему синусов:
где — радиус окружности, описанной около треугольника
Выразим радиус и подставим известные значения:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Биссектриса угла треугольника
пересекает его сторону
в точке
и его описанную окружность в точке
а) Докажите, что треугольник — равнобедренный.
б) Найдите радиус окружности, описанной около треугольника если
и
Источники:
а) Углы и
равны как вписанные углы, опирающиеся на одну дугу
Аналогично углы и
равны как вписанные углы, опирающиеся на
одну дугу

Так как — биссектриса угла
треугольника
то углы
и
равны. Таким образом, получаем равенство:
Тогда в треугольнике углы
и
равны, следовательно, он
равнобедренный с основанием
б) Запишем для треугольника теорему косинусов:

Выразим косинус угла и подставим известные значения:
Из основного тригонометрического тождества:
Далее, углы и
равны как вписанные углы, опирающиеся на одну
дугу
значит, их синусы также равны.
Так как биссектриса угла треугольника делит противолежащую сторону на
отрезки, пропорциональные прилежащим сторонам, то для треугольника
имеем:
Тогда с учетом того, что получаем
Запишем для треугольника теорему синусов:
Здесь — радиус окружности, описанной около треугольника
Выразим радиус и подставим известные значения:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
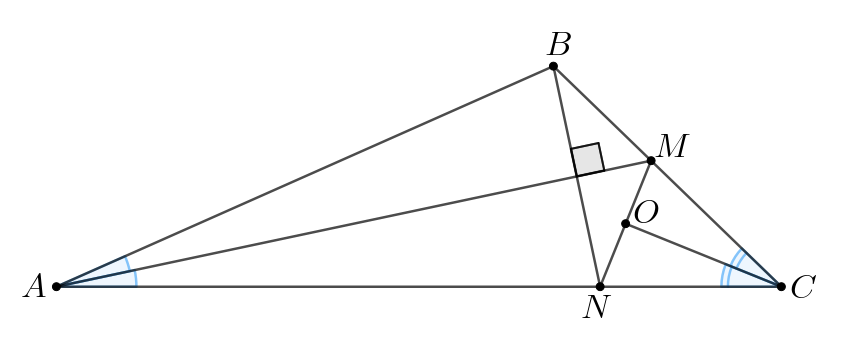
В треугольнике проведена биссектриса
Прямая, проходящая через
вершину
перпендикулярно
пересекает сторону
в точке
При
этом
а) Докажите, что биссектриса угла делит отрезок
пополам.
б) Пусть — точка пересечения биссектрис треугольника
Найдите
отношение
Источники:
а) Докажем, что Тогда в равнобедренном
биссектриса
также будет и медианой, то есть получим
Заметим, что равнобедренный, так как
— прямая, содержащая
биссектрису и высоту. Следовательно,
Тогда получаем
Так как биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, то имеем:
Также известно, что следовательно, из двух полученных
равенств находим
Таким образом, мы доказали, что
а
значит, в равнобедренном
биссектриса
делит сторону
пополам.
б) Заметим, что из доказанного в пункте а) следует, что Тогда в
отрезок
— медиана и высота, следовательно, этот треугольник
равнобедренный и
Таким образом, вместо отношения
можно искать отношение
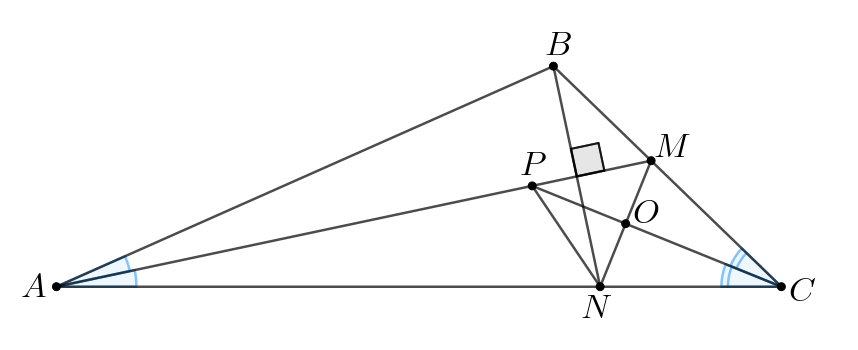
Отрезок является биссектрисой угла
следовательно, он делит
сторону
на отрезки, пропорциональные прилежащим сторонам, то
есть
б) 4
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |


