.00 №18 из ЕГЭ 2025
Ошибка.
Попробуйте повторить позже
Найдите все значения при каждом из которых уравнение
имеет ровно одно решение или не имеет решений вовсе.
Источники:
Для начала заменим для удобства на
Пусть левая часть уравнения — функция
Пусть правая часть уравнения — функция
Так как уравнение останется прежним, если заменить на
то
можем решать задачу для
а затем добавить в ответ все значения
противоположного знака.
Нарисуем графики этих функций в осях
Функция четная, убывает при
и возрастает при
При
функция принимает значение
Рассмотрим функцию
Ее модули обнуляются при и
Так как мы рассматриваем
то
Тогда, раскрыв модули, получаем:
Это «корыто» с ветвями вверх, дно которого лежит на прямой
Заметим, что
также четна:
При этом так как ветви корыта лежат на фиксированных прямых, то при изменении параметра его дно двигается вверх/вниз, а границы дна «скользят» по этим фиксированным прямым.
Итак, нарисуем оба графика и изобразим граничные положения. Так
как обе функции четны, то рисунок будет симметричен относительно оси
При вершина функции
находится в точке
а корыто
принимает вид
то есть представляет собой галочку.
Получаем следующую картинку:
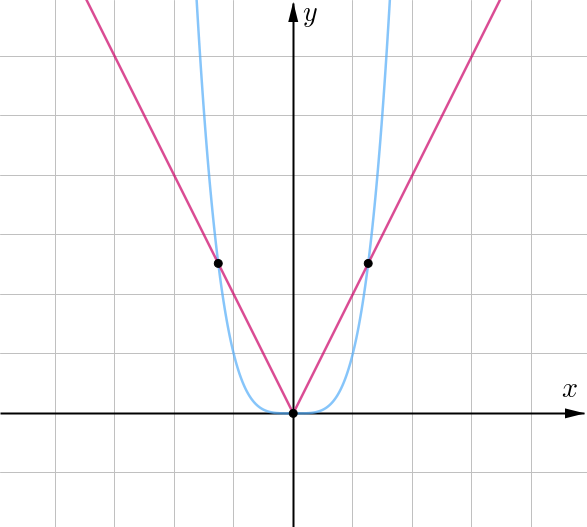
Заметим, что в таком случае получается 3 решения, то есть нам не
подходит.
Далее вершина графика находится в точке
а дно корыта
лежит на прямой
Поймем, когда вершина
будет ниже дна корыта, а
когда выше:
Таким образом, при вершина
ниже дна
при
лежит на дне, при
выше дна.
Когда вершина находится ниже дна корыта
то очевидно при
будет пересечение
и
а так как рисунок симметричен
относительно
то и при
будет пересечение. Тогда решений будет как
минимум 2, то есть значения
нам не подходят.
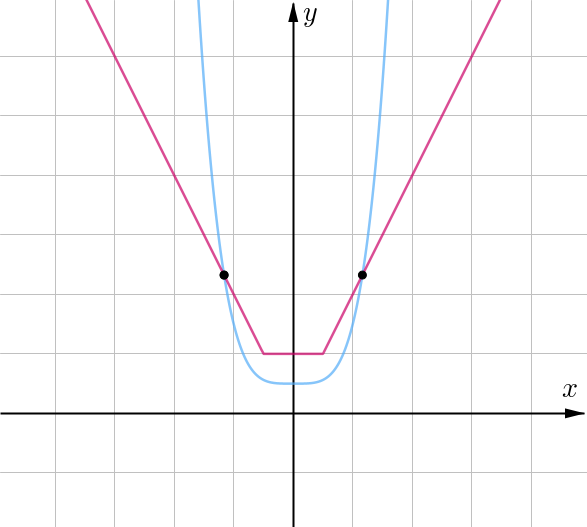
Нарисуем случай Как мы уже поняли, в этом случае вершина
лежит на дне корыта
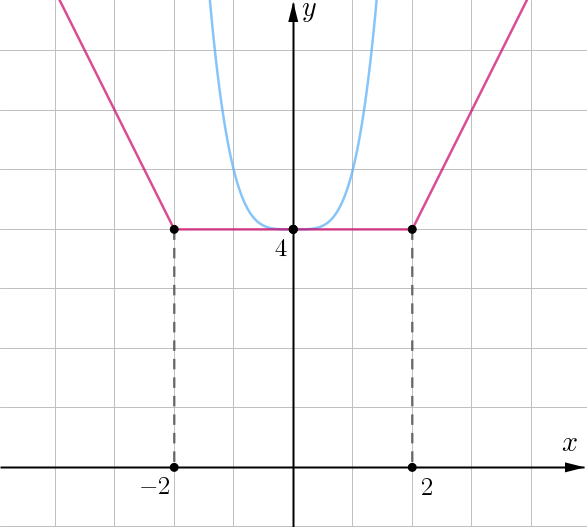
Поймем, что в этом случае правая ветвь не имеет пересечений с правой
ветвью корыта
Действительно, во-первых,
во-вторых, при
функция
возрастает быстрее, чем правая ветвь
Таким образом, в данном случае при графики не пересекаются и, в силу
симметрии, не пересекаются и при
То есть при
одна точка
пересечения
значит, это значение параметра подходит.
При вершина
выше дна корыта
Поймем, что в данном
случае решений уже не будет. Так как вершина
выше дна корыта
то
не пересекает дно корыта
Покажем, что при
не
пересекает правую ветвь корыта
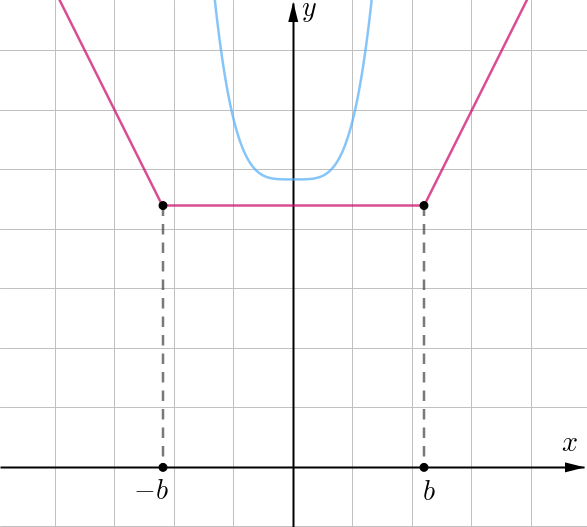
Действительно, во-первых, во-вторых, при
функция
возрастает быстрее, чем правая ветвь
Таким образом, в данном случае при графики не пересекаются и, в силу
симметрии, не пересекаются и при
То есть при
пересечений вовсе
нет, значит, эти значения параметра подходят.
Объединяя подходящие значения, и добавив значения, противоположные по знаку, получаем:
Так как получаем в итоге:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




