Вступительные в МГУ 2010 и ранее
Ошибка.
Попробуйте повторить позже
Какую максимальную площадь может иметь четырёхугольник, стороны которого последовательно равны ,
Найти все значения
при которых она достигается.
Источники:
Подсказка 1
Не очень понятно, как искать площадь четырёхугольника, про который мы практически ничего не знаем. Давайте попробуем разбить нашу фигуру на фигуры поменьше и попроще.
Подсказка 2
Проведём диагональ и получим два треугольника, у каждого из них мы знаем по две стороны. Обозначим углы между этими сторонами как α и β и посчитаем площадь. Как теперь можно оценить полученное выражение?
Подсказка 3
Верно, мы знаем, что синус не больше единицы! Запишем неравенство и найдём максимальное значение площади. А когда достигается такое значение?
Подсказка 4
Правильно, когда углы α и β прямые! Но тогда фигуры, которые мы получили — это два прямоугольных треугольника с общей гипотенузой. Запишите для них теорему Пифагора и приравняйте гипотенузы, чтобы найти а. Не забудьте проверить, что при найденных значениях все стороны исходного четырёхугольника положительны.
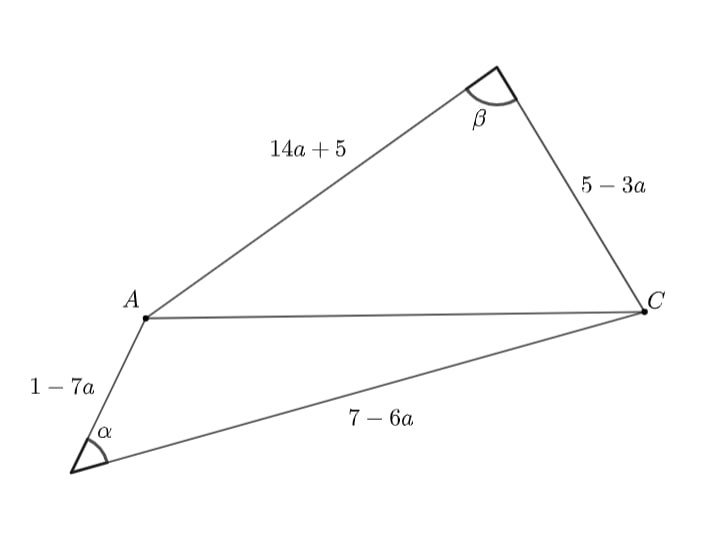
Пусть — площадь данного четырёхугольника,
— угол между соседними сторонами, равными
и
а
— угол между
соседними сторонами, равными
и
Тогда
Оценка достигается при ведь иначе знак неравенства изменится на строгий и
Итак, максимальную площадь
имеет четырёхугольник, составленный при
из двух прямоугольных треугольников с катетами
и
с
общей гипотенузой, поэтому
Если то одна из сторон четырёхугольника окажется отрицательной
Этого быть не может.
При действительно, поскольку
условию задачи удовлетворяет четырёхугольник, составленный из двух
прямоугольных треугольников с катетами 1, 7 и 5, 5 с общей гипотенузой, равной
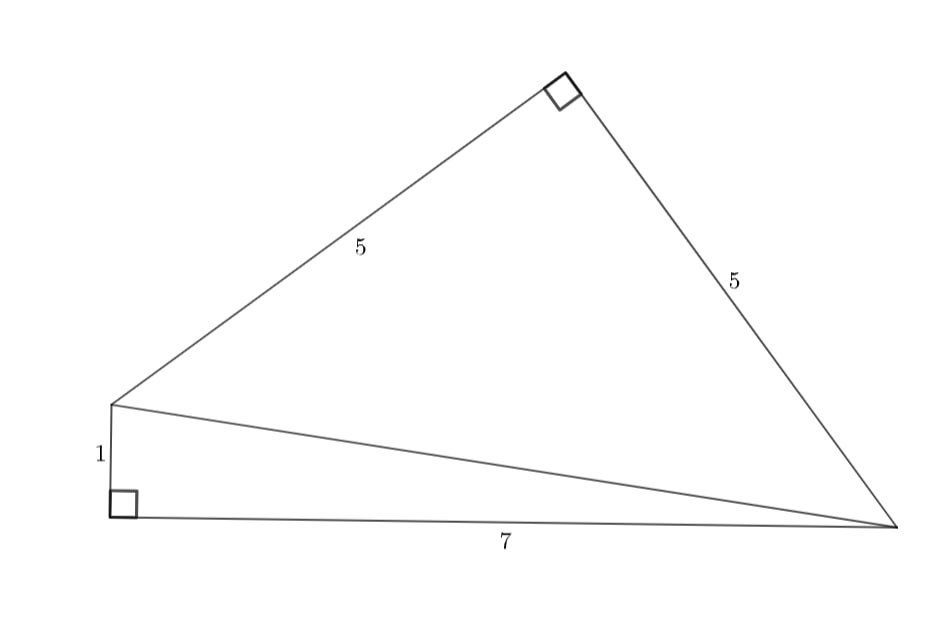
16 при
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




