Вступительные в МГУ 2010 и ранее
Ошибка.
Попробуйте повторить позже
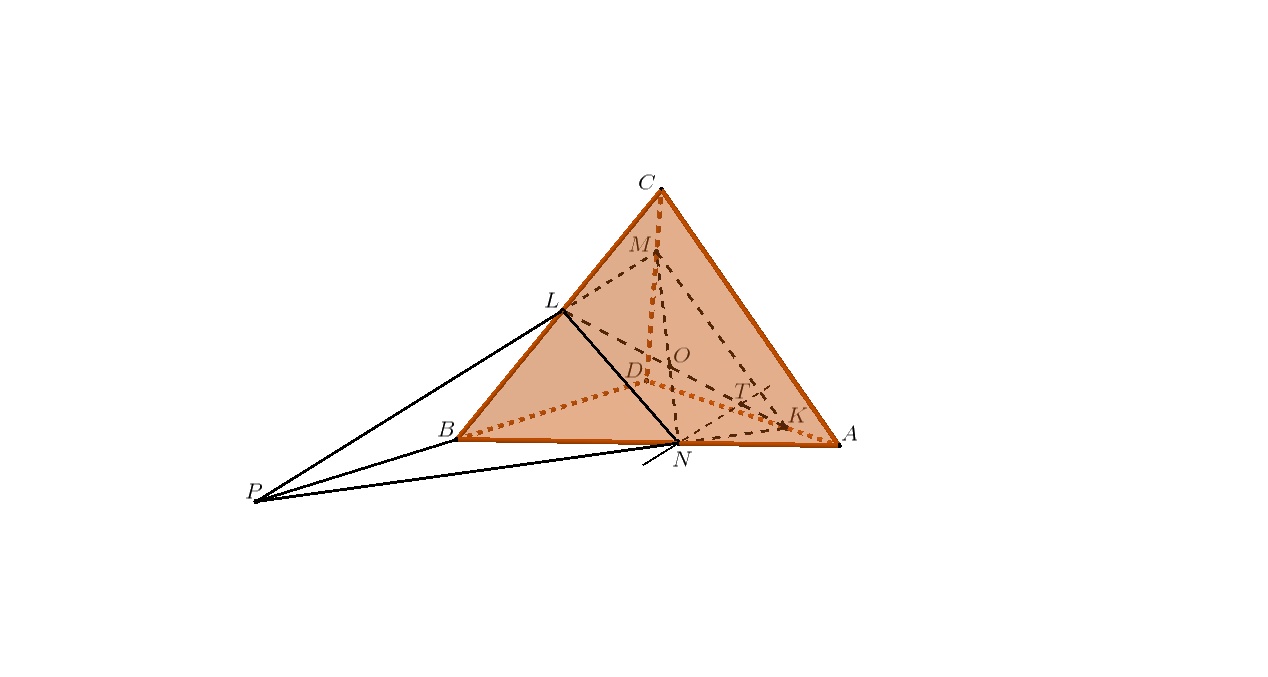
В пирамиде проведено сечение
так, что точка
лежит на ребре
точка
— на ребре
точка
— на ребре
точка
на ребре
и
— точка пересечения диагоналей
и
четырехугольника
Сечение
делит
пирамиду на две части. Найти отношение объемов этих частей, если известны следующие соотношения между длинами
отрезков:
Источники:
Подсказка 1
Одно из соотношений в условиях выглядит немного страшным, может быть, его можно как-то преобразовать в более приятный вид?
Подсказка 2
Заметим, что в нем два отрезка повторяются особенно часто, почему бы не поделить всё равенство на них?
Подсказка 3
Оба многогранника, отношение объёмов которых нужно найти, имеют на самую приятную форму, а значит, и их объёмы будет искать весьма неприятно, может быть, как-то можно сократить количество "неприятных" работ?
Подсказка 4
Если один из объёмов сможем выразить через объем пирамиды ABCD, то сможем сразу получить и второй! Самое время подумать, как можно выразить, например, объем многогранника DBKMLN через объем ABCD. Может быть, помогут какие-то доппостроения?
Подсказка 5
Объем сложных многогранников часто легко найти через сумму/разность более "простых", например, тетраэдров. Какими должны быть эти тетраэдры, чтобы можно было легко выразить один объем через другой?
Подсказка 6
Если два тетраэдра имеют общий трёхгранный угол, то отношение их объёмов будет равно отношению произведения трёх соответствующих рёбер, образующих трёхгранный угол. Поэтому давайте достроим наш многогранник DBKMLN до тетраэдра, имеющего общий угол с нашей пирамидой ABCD, соединив, например, прямые KN и ML в точке Р (не забудьте проверить, с какой стороны они будут пересекаться).
Подсказка 7
Получается, что мы сможем выразить объем DBKMLN через объем ABCD, если сможем выразить объем DKMP через объем ABCD, а объём DBKMLN через объём DKMP (что тоже можем сделать через разность "приятных" объёмов!). Значит, что необходимо знать, чтобы получилось выразить необходимые отношения объёмов?
Подсказка 8
Теперь осталось посчитать, в каких отношениях точки N, L, K, B и M делят соответственно отрезки PK, PM, AD, PD и CD, на которых они лежат. И тогда легко найти отношения длин рёбер, образующих нужные нам трёхгранные углы. А какая теорема лучше всего подходит для поиска отношений?
Подсказка 9
Да, именно теорема Менелая — у нас просто огромное количество треугольников и секущих, подходящих для её применения! Почему бы тогда не записать её для тех треугольников и секущих, для которых получатся нужные нам отношения или отношения, из которых легко получится посчитать нужные нам?
Подсказка 10
Почему бы не начать с треугольника KLP и секущей MN, для которых мы знаем по крайней мере одно из отношений сторон? Очевидный, но неочевидно полезный факт: (a+b)/b=a/b+1. Попробуйте записать равенство так, чтобы получилось его использовать.
Подсказка 11
Одно отношение мы знаем, но все равно остается еще два неизвестных нам отношения. Тогда почему бы не записать теорему Менелая для другого треугольника, в которой тоже будут участвовать эти же или связанные с ними отношения? (не забываем про неочевидно полезный факт)
Подсказка 12
С помощью неочевидно полезного факта из одной теоремы для треугольника KLP можно выразить PN/NK через PL/LM, а из второй для треугольника NMP — PL/LM через PN/NK. Осталось подставить одно в другой и найти PL/LM и PN/NK!
Подсказка 13
Теперь можно сделать что-то похожее для точек K, B и M. Какие треугольники стоит выбрать? Стоит обратить внимание на то, про какие отношения нам известно больше всего информации.
Подсказка 14
Из условия, преобразованного чуть ранее, известна связь между DK/KA и BN/NA, поэтому стоит выбрать треугольник, в котором участвует хотя бы одно из них (если не оба). И сразу по аналогии с нашими предыдущими действиями запишем и теорему Менелая для "парного" треугольника (не забудем про неочевидно полезный факт)
Подсказка 15
Получилось два равенства: одно для треугольника KDP, а второе для треугольника ADB. Как можно использовать равенство из условия, чтобы максимально сократить количество неизвестных отношений?
Подсказка 16
В отличие от DK/KA отношение BN/NA встречается только один раз, поэтому давайте избавимся от него! Теперь осталось два уравнения с двумя неизвестными отношениями DB/BP и DK/KA, которые можно и нужно найти :)
Подсказка 17
Осталось найти только, в каком отношении точка М делит CD, почему бы еще раз не "поменелаить"?) Считаем и легко выражаем нужные объёмы!
Подсказка 18
Наконец, зная все отношения, легко выразить объемы DKMP через ABCD, BLNP через DKMP и DBKMLN через разность DKMP и BLNP. Находим отношение объёмов ACKMLN и DBKMLN и празднуем победу!
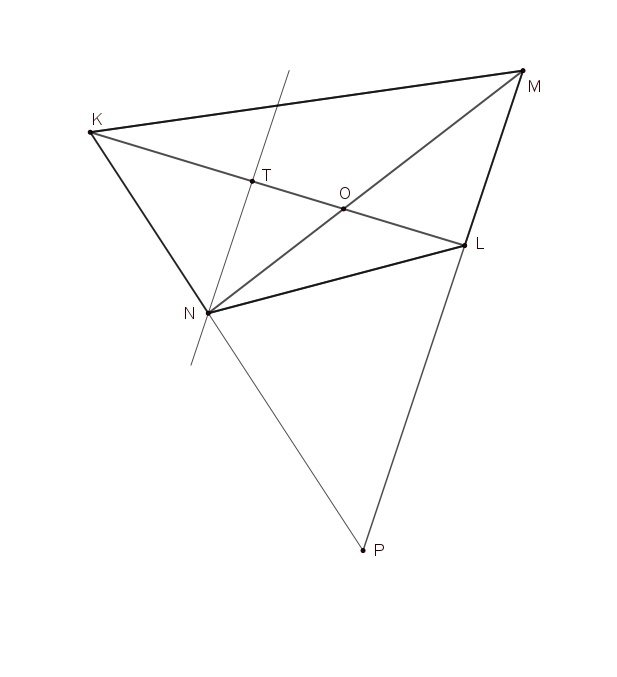
Преобразуем соотношение из условия:
Рассмотрим плоскость Проведем прямую
такую, что
||
где
— точка пересечения прямых
и
Тогда
подобен
откуда
следовательно, точка
лежит внутри отрезка
откуда
понимаем, что прямые
и
пересекутся под прямой
в точке
Кроме того, плоскости
и
попарно
пересекаются, значит, прямая
тоже пройдет через точку
Выразим через второй нужный объем и объем пирамиды
:
Заметим также, что
Причем можно выразить
, а
— через
:
Чтобы понять, в каких отношениях точки и
поделили отрезки
и
соответственно, запишем теорему Менелая для
и секущей
:
Запишем также теорему Менелая для и секущей
:
Отсюда получаем, что
Чтобы найти, в каком отношении точки и
делят отрезки
и
соответственно, запишем теорему Менелая для
и
секущей
:
Также запишем теорему Менелая для и секущей
:
Теперь найдем и
Осталось только найти, в каком отношении точка делит отрезок
Для этого запишем теорему Менелая для
и секущей
:
И наконец найдем нужные отношения объемов:
Откуда можем выразить :
Получается, что искомое отношение объемов:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




