Вступительные в МГУ 2010 и ранее
Ошибка.
Попробуйте повторить позже
Вписанная в треугольник окружность касается его сторон в точках
и
Известно, что в треугольнике
угол
равен
произведение всех сторон равно
а вершина
делит отрезок
пополам. Найдите длины сторон треугольника
Источники:
Подсказка 1
Для начала стоит задуматься о том, что вообще может нам дать условие про вписанную окружность, как мы можем воспользоваться тем, что стороны треугольника являются касательными к ней?
Подсказка 2
Отрезки касательных, проведенных из одной точки, равны. Запишем этот факт для всех касательных и дополнительно учтем условие AK=KC. Какой вывод можем сделать?
Подсказка 3
Треугольник АВС является равнобедренным. Отсюда же понимаем, что N и M делят боковые стороны в равных отношениях
Подсказка 4
В итоге имеем, что AC || NM. Также, используя факт об угле между хордой и касательной, мы получаем большой простор для счета углов!
Подсказка 5
Теперь надо воспользоваться условием на произведение сторон △KMN. Стандартный подход: выразить все стороны через одну неизвестную. Удобно в качестве нее взять радиус описанной окружности около KMN.
Подсказка 6
Мы знаем все углы треугольника, тогда можем выразить все стороны с помощью теоремы синусов!
Подсказка 7
Теперь нужно стороны △АВС выразить через стороны △KMN, которые мы знаем. В таких ситуациях очень часто спасает подобие треугольников!
Подсказка 8
Из подобия △ANK и △KMN можем найти AK, а из подобия △ABC и △KMN найдем NM (не забывайте про равные отрезки касательных!)
Так как — точки касания вписанной окружностью сторон треугольника
то
Из
следует, что
а в треугольнике
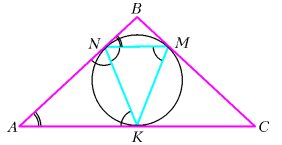
Вписанная в треугольник окружность является описанной около треугольника
Пусть
— ее радиус,
тогда
Вычисляя произведение находим, что
Угол как угол между касательной и хордой, равен углу
так что
поэтому треугольники
и
подобны. Следовательно,
значит, Наконец, из подобия равнобедренных треугольников
и
вытекает равенство
Таким образом,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




