Физтех 2016
Ошибка.
Попробуйте повторить позже
Точки 
последовательно расположены на прямой. Известно, что 
, 
. Окружности 
и 
,
касающиеся друг друга, таковы, что 
проходит через точки 
и 
, а 
проходит через точки 
и 
. Найдите радиусы
окружностей 
и 
, если известно, что их центры и точка 
лежат на одной прямой.
Обозначим центры окружностей 
и 
через 
и 
соответственно. Поскольку 
— середина хорды 
окружности 
, то отрезок
перпендикулярен 
. Опустим из точки 
перпендикуляр 
на прямую 
. Тогда 
(диаметр,
перпендикулярный хорде, делит эту хорду пополам).
Пусть 
. Тогда 
(так как 
— средняя линия треугольника 
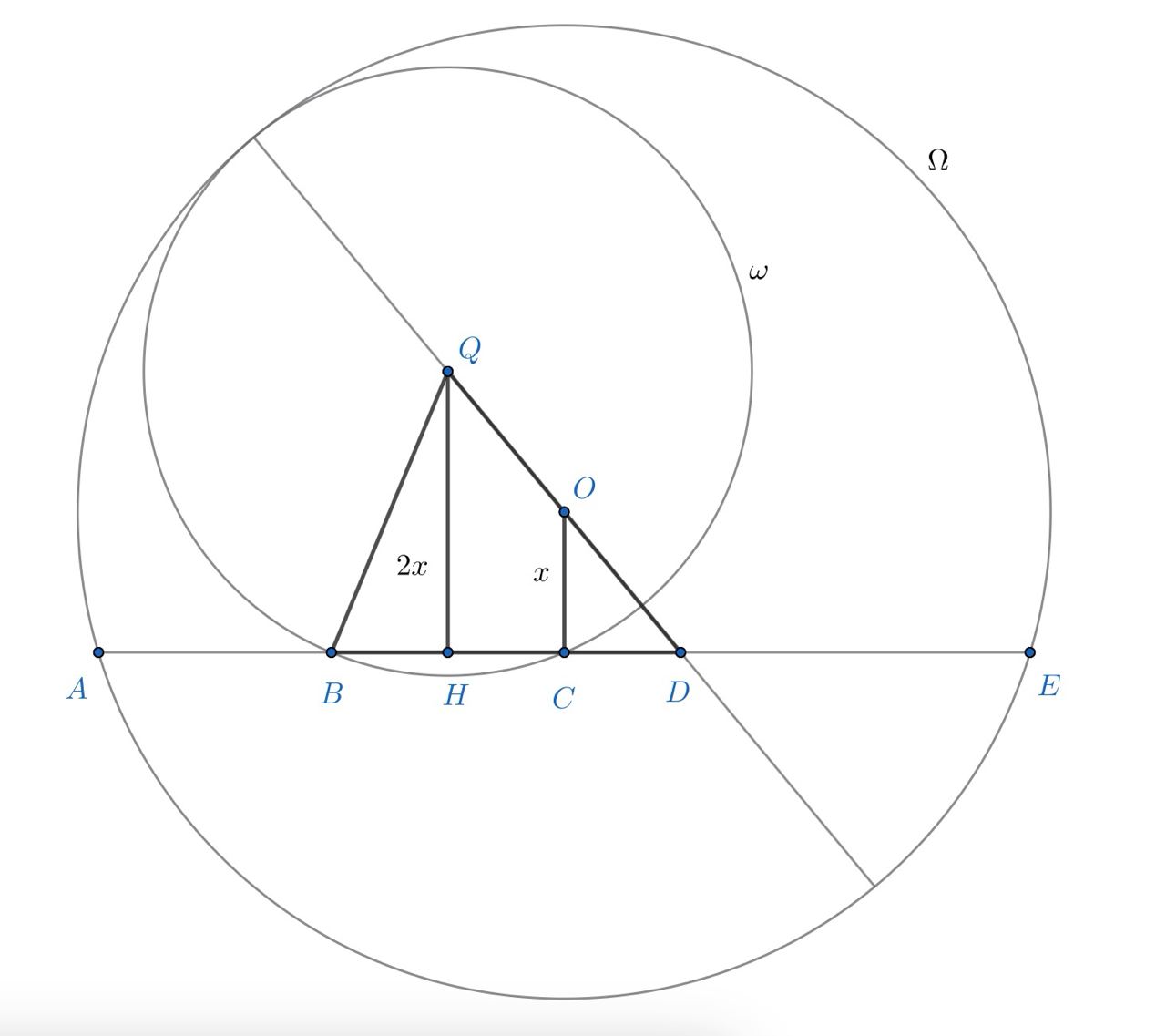
Выразим двумя способами отрезок 
. С одной стороны, так как окружности касаются внутренним образом, расстояние между их
центрами равно разности радиусов, т.е. 
. С другой стороны, из прямоугольной трапеции 
получаем,
что
Значит,
откуда
При условии 
получаем
Тогда получаем, что 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
