Физтех 2015

Рассмотрим все диагонали (или стороны) и разобьем их на группы параллельных. Такие группы бывают 2 видов: те, которые содержат диаметр и те, которые не содержат. Первых групп всего 11 (количество различных диагоналей, проходящих через центр) и в каждой из них по 10 диагоналей. Вторых групп тоже 11, но в каждой из них по 9 диагоналей.

Вторых групп тоже 11, но в каждой из них по 9 диагоналей (см. рис).

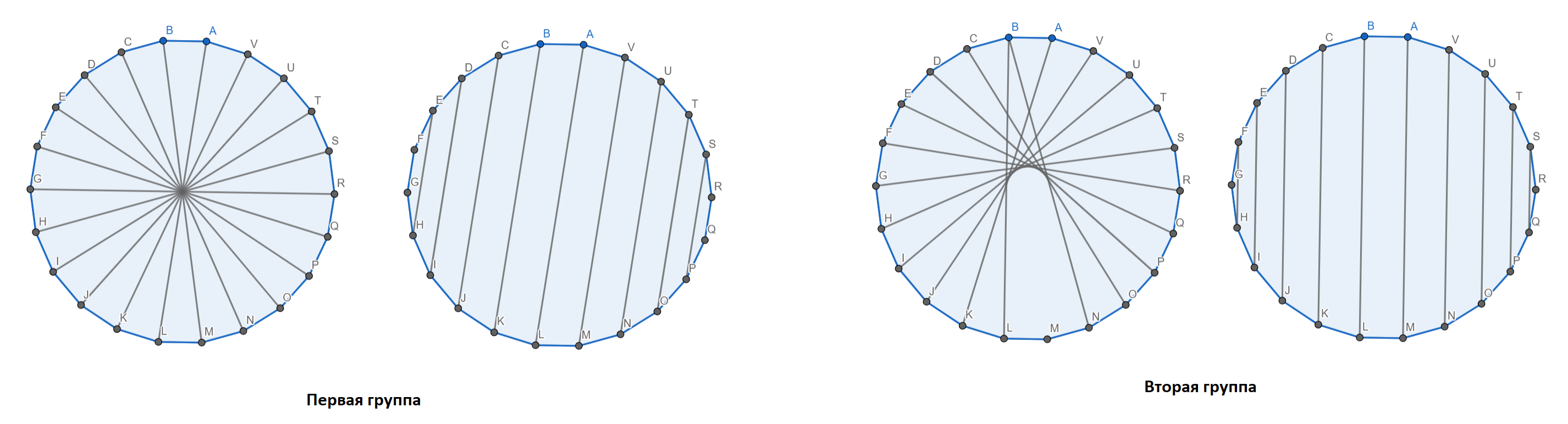
Для того, чтобы выбрать выпуклый четырёхугольник, у которого есть хотя бы одна пара параллельных сторон, нужно выбрать две параллельные диагонали (или стороны) и составить из них трапецию. Так мы получим четырехугольников. Осталось проверить, что они различны. На самом деле если наш четырехугольник имеет две пары параллельных прямых (вписанный параллелограмм — это прямоугольник), то он был посчитан два раза. Значит, из этого числа нужно вычесть количество прямоугольников. Выбрать прямоугольник можно таким способом. Сначала выберем 2 его соседние вершины. Это можно сделать способами, так как соседние вершины не могут быть противоположными, а затем однозначно определим оставшиеся 2 вершины, так как диагональ прямоугольника должна проходить через центр окружности. Так, каждый прямоугольник мы посчитаем раз и поэтому всего прямоугольников .

Получаем ответ .