Турнир городов 2015 и ранее
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике на высоте
выбрана произвольная точка
Точки
и
– середины сторон
и
соответственно. Перпендикуляр, опущенный из
на
пересекается с перпендикуляром, опущенным из
на
в точке
Докажите, что точка
равноудалена от точек
и
Подсказка 1
Обозначим через R и Q основания перпендикуляров, опущенных из M и N. Попробуйте переформулировать условие задачи.
Подсказка 2
Например, можно доказать, что точка P будет лежать на серединном перпендикуляре к AC.
Подсказка 3
Есть ли теорема, которая может нам в этом помочь?
Подсказка 4
Вспомните о теореме Карно.
Подсказка 5
Её можно применить для треугольника AXC, но должно выполняться CP² + XR² = XQ² + AR². Как бы нам это доказать?...
Подсказка 6
Может, надо записать теорему Пифагора для каких-то треугольников?
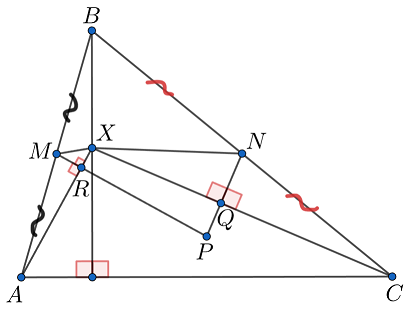
Обозначим через и
основания перпендикуляров, опущенных из
и
Достаточно показать, что
тогда по теореме Карно для треугольника
точка
будет лежать на серединном перпендикуляре к
что равносильно
требуемому. Выразим квадраты из равенства с помощью теоремы Пифагора для треугольников
и
:
Приведём подобные:
Домножим равенство на запишем
как
как
а квадраты
и
распишем с помощью формулы
медианы для треугольников
и
Приведём подобные и поделим на
Это равенство верно, поскольку
получили требуемое.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




