Тема ММО - задания по годам

ММО 2019

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#73172

Биссектриса угла $ABC$ пересекает описанную окружность $ω$ треугольника $ABC$ в точках $B$ и $L$ . Точка $M$ — середина отрезка $AC$ . На дуге $ABC$ окружности $ω$ выбрана точка $E$ так, что $EM ∥ BL$ . Прямые $AB$ и $BC$ пересекают прямую $EL$ в точках $P$ и $Q$ соответственно. Докажите, что $PE = EQ$ .

Источники: ММО-2019, 9.5

Подсказки к задаче

Подсказка 1

Рассмотрите точки пересечения EM с AB и BC . Обозначьте все равные углы, какие сможете найти.

Подсказка 2

Мы хотим доказать равенство сторон, но по сути знаем только углы. Что можно сделать?

Подсказка 3

Попробуйте воспользоваться теоремой синусов.

Показать доказательство

Пусть прямая $EM$ пересекает $AB$ и $BC$ в точках $P′$ и $Q′$ соответственно. Также обозначим

′ ′ α= ∠BAE = ∠BLE = ∠BCE = ∠QEQ = ∠PEP

′ ′ β = ∠ABL = ∠CBL =∠AP E = ∠BQ E

(использовали равные опирающиеся на одну дугу углы и углы при параллельных прямых)

$PIC$

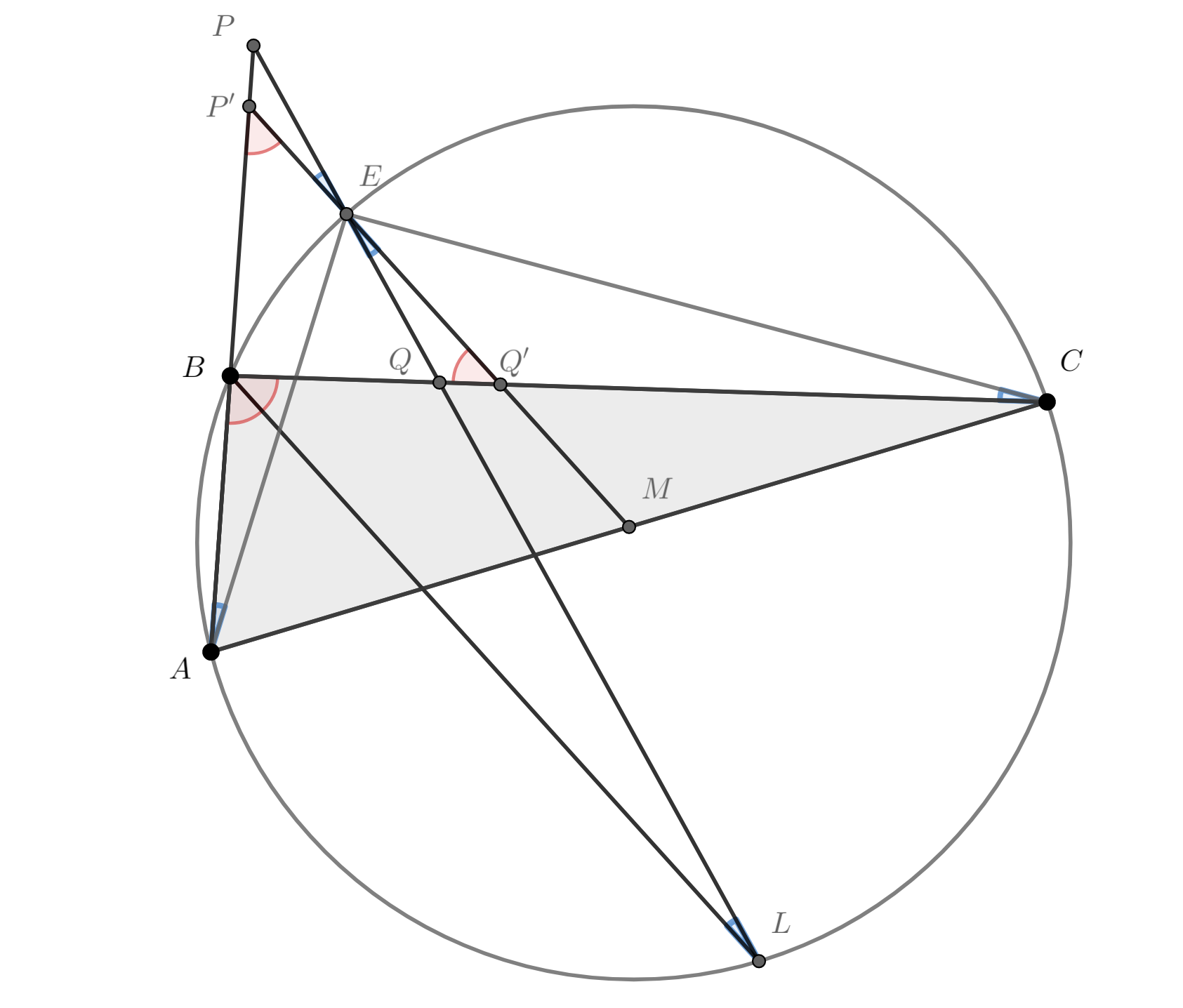
Последовательно применяя теорему синусов для треугольников $PP′E$ , $AP ′E$ и $AP ′M$ , получим:

PE = P′E⋅sin-β= --AP-′⋅sinα-⋅sinβ-- = sin(β− α) sin(β+ α)⋅sin(β − α)

AM sin∠EMC ⋅sinαsin β AC ⋅sin∠EMA ⋅sinα = sinβ-sin(β-+α)sin(β−-α) = 2⋅sin(β+-α)⋅sin(β-− α)

Аналогично, применяя теорему синусов для треугольников $QQ ′E$ , $CQ′E$ и $CQ ′M$ , получим:

CM-⋅sin∠EMC--⋅sinα-⋅sinβ -AC-⋅sin∠EMA--⋅sinα- QE = sin β⋅sin(β +α)⋅sin(β− α) = 2⋅sin(β+ α)⋅sin(β − α) =P E

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#79749

Докажите, что для любого натурального числа $n >2$ и для любых действительных чисел $a ,a ,...,a, 1 2 n$ удовлетворяющих условию $a1+ a2+ ...+an ⁄=0,$ уравнение

a1(x − a2)(x− a3)...(x − an)+

+a2(x− a1)(x− a3)...(x− an)+...+

+a (x − a )(x− a )...(x − a )= 0 n 1 2 n−1

имеет хотя бы один действительный корень.

Источники: ММО-2019, 11.4(см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Что можно сказать о левой части уравнения?

Подсказка 2

Заметим, что это многочлен степени n-1. Какие случаи можно рассмотреть?

Подсказка 3

Например, если бы n было чётным, то всегда бы нашелся хотя бы 1 действительный корень.

Подсказка 4

Пусть n — нечётно. Что тогда можно сказать про a-шки?

Подсказка 5

Если бы нашлись такие i и j, что aᵢ = aⱼ, то был бы корень a = aᵢ = aⱼ. Поэтому будем считать a-шки различными. Что, если для некоторого i aᵢ = 0?

Подсказка 6

Тогда aᵢ — корень. Будем считать a-шки ненулевыми. Упорядочим их по возрастанию.

Подсказка 7

Попробуйте посмотреть на знак выражения при подстановке aₖ вместо x.

Показать доказательство

Левая часть $f(x)$ в этом уравнении представляет собой многочлен степени $n− 1,$ так как коэффициент при $xn−1$ равен $a1+ ...+ an ⁄= 0.$ Если $n$ четно, то получаем многочлен нечетной степени, он всегда имеет действительный корень, так как функция $f(x)$ непрерывна и $f(x0) >0,f(− x0)< 0$ при достаточно большом $x0 > 0.$ Пусть $n$ нечетно. Можно считать, что все числа $a1,...,an$ различны (в противном случае число $a= ai = aj,$ где $i⁄= j,$ является корнем), не равны нулю (если $ai = 0$ при некотором $i,$ то и $f(ai)= 0$ ) и упорядочены по возрастанию: $a1 <a2 < ...< an.$ Заметим, что

f(ak)= ak(ak− a2)...(ak − ak−1)(ak− ak+1)...(ak− an)

имеет тот же знак, что и $n−k k−1 ak ⋅(−1) = (− 1) ak.$ Но при $n > 3$ среди чисел $a1 < a2 < ...< an$ есть хотя бы одна пара соседних, имеющих одинаковый знак. Тогда значения в этих точках разного знака, поэтому между ними есть корень многочлена $f(x).$

Ошибка.
Попробуйте повторить позже

Задача 3#84475

В остроугольном треугольнике $ABC$ проведены высоты $AA′$ и $BB′$ , точка $O$ — центр его описанной окружности. Докажите, что расстояние от точки $′ A$ до прямой $BO$ равно расстоянию от точки $′ B$ до прямой $AO$ .

Подсказки к задаче

Подсказка 1

Пусть α, β, γ — углы треугольника при вершинах A, B и С соответственно. Попробуйте повыражать углы.

Подсказка 2

Воспользуйтесь свойством ортоцентра и тем, что треугольник ABB' — прямоугольный.

Подсказка 3

Выразите AK' через другую сторону и тригонометрические функции.

Подсказка 4

Воспользуйтесь тем, что O — центр описанной окружности и треугольника AOC.

Показать доказательство

Введём обозначения, $α,$ $β,$ $γ$ — углы треугольника при вершинах $A,B,C$ соответственно.

По свойству ортоцентра и тому, что треугольник $′ ABB$ прямоугольный получаем

′ ′ ∘ ′ ∘ ∠A BK = ∠ABB =90 − ∠BAB =90 − α

Значит, так как треугольник $A′BK$ прямоугольный

A ′K = A′B sin(90∘− α)= A′Bcosα

А из прямоугольного треугольника $AA ′B$ получаем, что

A′B = AB cosβ

Подставив эти равенства одно в другое, в итоге получим, что

A′K = AB cosβ cosα

$PIC$

Теперь из того, что $O$ — центр описанной окружности и равнобедренного треугольника $AOC,$ в котором $AO = CO$ как радиусы, выражаем

′ ∘ ∠AOC- ∘ 2∠ABC- ∘ ∠B AT = 90 − 2 = 90 − 2 = 90 − β

Так как треугольники $′ AB T$ и $′ ABB$ прямоугольные, то

B ′T = AB′sin(90∘− β)= AB′cosβ = ABcosαcosβ

Видно, что

′ ′ A K = BT = AB cosαcosβ

Ошибка.
Попробуйте повторить позже

Задача 4#91949

Каждая точка плоскости раскрашена в один из трех цветов. Обязательно ли найдется треугольник площади $1,$ все вершины которого имеют одинаковый цвет?

Источники: ММО - 2019, 10.4(см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Предположим, что искомого треугольника не существует. Ясно, что если зафиксировать любую прямую, то на ней найдется две точки A и B одного цвета (назовем его цветом 1). Где может располагаться третья точка, которая образовывала бы с найденным точками треугольник единичной площади?

Подсказка 2

Пусть расстояние между точками A и B равно d. Тогда искомая точка может располагаться на любой из прямых, расположенных от данной на расстоянии 2/d, (назовем их l₁ и l₂). По предположению, точек цвета 1 на данных прямых нет. А могут ли на прямой AB находится точки цветов, отличных от 1, если на каждой из прямых l₁ и l₂ присутствует 2 и 3 цвет?

Подсказка 3

Несложно показать, что это не могут (разберите случай, когда любые две точки на прямых l₁ и l₂, расстояние между которыми равно d/2, имеют разный цвет и противный ему). Какое естественное свойство при этом накладывается на одну из прямых AB, l₁ и l₂?

Подсказка 4

По крайней мере на одной из этих прямых все точки имеют один и тот же цвет. Что можно сказать о цветах остальных точек плоскости?

Подсказка 5

Они покрашены в цвет, отличный от данной прямой. Как теперь можно завершить решение?

Показать ответ и решение

Первое решение. Предположим, что такого треугольника не существует, и докажем, что существует прямая, все точки которой имеют один цвет.

Пусть на некоторой прямой $l$ есть две точки $A,B$ одного цвета (обозначим этот цвет $1),$ расстояние между которыми равно $d.$ Пусть $l1,l2$ — две прямые, параллельные $l$ и удаленные от нее на расстоянии $2∕d.$ Если на какой-нибудь из этих прямых есть точка цвета $1,$ то она образует с точками $A,B$ треугольник площади $1,$ все вершины которого имеют одинаковый цвет. Если на каждой из прямых $l1,l2$ присутствуют два цвета и на одной из них найдутся две точки одного цвета на расстоянии $d∕2,$ то они вместе с точкой такого же цвета на другой прямой образуют треугольник площади $1,$ все вершины которого имеют одинаковый цвет. Если же на каждой из прямых $l1,l2$ присутствуют два цвета и любые две точки на расстоянии $d∕2$ разных цветов, то любые две точки на расстоянии $d$ будут одного цвета, а значит, на прямой $AB$ все точки имеют цвет $1.$

Пусть теперь все точки некоторой прямой $a$ покрашены в цвет $1.$ Тогда остальные точки плоскости покрашены в два оставшихся цвета. Возьмем прямую, не параллельную $a,$ и две точки $C,D$ на ней одного цвета (обозначим этот цвет $2).$ Если на какой-нибудь из двух прямых, параллельных $CD$ и удаленных от нее на расстояние $2∕CD,$ найдется точка цвета $2,$ то $C,D$ и эта точка образует треугольник площади $1,$ все вершины которого имеют одинаковый цвет. Если же таких точек нет, то найдется треугольник площади $1$ с вершинами цвета $3.$

______________________________________________________________________________________________________________________________________________________

Второе решение. Пусть не все точки плоскости раскрашены в один цвет. Тогда на некоторой прямой присутствуют точки разных цветов: точки $A$ и $B$ цвета $1$ и точка $X$ цвета $2.$ Пусть $A1B1B2A2$ — прямоугольник, в котором $A,B$ середины сторон $A1A2,B1B2$ соответственно, длины этих сторон равны $4∕AB,C1,C2$ — середины $A1B1$ п $A2B2$ соответственно, $D$ — точка, симметричная $C1$ относительно $B1.$

Если среди точек $A1,B1,C1,A2,B2,C2$ есть точка цвета $1,$ она образует искомый треугольник с точками $A,B.$ Если среди точек $A1,B1,C1,A2,B2,C2$ нет точек цвета $1,$ то возможны следующие случаи.

1.: Точки $A1$ и $B1$ (рассуждение для точек $A2$ и $B2$ аналогичны) разного цвета. Тогда цвет $C1$ совпадает с цветом одной из них, например, $A1.$ Если какая-то из точек $A2,C2$ того же цвета, эти три точки образуют искомый треугольник. В противном случае искомым будет треугольник $A2C2B1.$
2.: Если одна из пар $A1,B1$ или $A2,B2$ цвета $2,$ она образует искомый треугольник с точкой $X.$
3.: Если все точки $A1,B1,A2,B2$ цвета $3$ и одна из точек $C1,D$ тоже цвета $3,$ то треугольник $B1C1B2$ или $B1DB2$ искомый. В противном случае треугольник $C1DX$ искомый.

Ответ:

да