Тема ММО - задания по годам

ММО 2017

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31222

Найдите наибольшее натуральное число, все цифры в десятичной записи которого различны и которое уменьшается в пять раз, если зачеркнуть первую цифру.

Источники: ММО-2017, 9.1, автор - М.А. Евдокимов, (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Попробуйте представить число так, чтобы оно имело вид суммы двух слагаемых, одно из которых-число после зачеркивания.

Подсказка 2

Да, мы представили n=a*10^(k-1)+m, где a-первая цифра, k-кол-во цифр. Но ведь тогда a*10^(k-1)=4m. Попробуйте оценить k, зная, что в числе нет одинаковых цифр.

Подсказка 3

Ура! Мы получили, что k<=4(так как иначе на конце будет две одинаковые цифры-нули). Остается перебрать варианты и выбрать максимальное число.

Показать ответ и решение

По условию $aA-= 5A$ (где $A−$ число, составленное из всех цифр, кроме первой, $a$ — первая цифра). Пусть $n$ – количество цифр в числе $--- aA.$ Отсюда

n−1 n−3 4A =a ⋅10 ⇒ A = 25a ⋅10

Если $n> 4,$ то у числа $A,$ а значит, и у искомого числа, есть две совпадающие цифры (два нуля на конце). Если же $n =4,$ то

A = 250a

Ясно, что чем больше $a,$ тем больше исходное число. При $a≥ 4$ число $250a$ состоит из $4$ цифр, а не из трех. При $a= 3$ мы получаем $A = 750,$ а исходное число равно $3750.$ Значит, наибольшее искомое число равно $3750.$

Ответ:

$3750$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#31351

Даны две непостоянные прогрессии $(a ) n$ и $(b), n$ одна из которых арифметическая, а другая — геометрическая. Известно, что $a1 = b1,a2 :b2 = 2$ и $a4 :b4 =8.$ Чему может быть равно отношение $a3 :b3?$

Источники: ММО-2017, 11.1, автор - Д.В. Горяшин, (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Вообще, у нас есть два случая: когда a_i - арифм. прогрессия, b_i - геом, и наоборот. Давайте в обоих случаях обозначим T - первые члены, d - разность арифм.прогрессии, q - разность геом.прогрессии. Как в первом случае будут переписаны условия через T, d и q?

Подсказка 2

Если подставить одно условие в другое, то можно получить уравнение на q! Проверьте все случаи, чему может быть равно q, и останется выразить d и третьи члены прогрессий

Подсказка 3

Теперь остаётся проверить второй случай: a_i - геом. прогрессия, b_i - арифм. прогрессия. Также перепишите условия, которые вам даны, в терминах T, d и q, и подставьте одно в другое)

Показать ответ и решение

Пусть $a = b = a⁄= 0 1 1$ , разность арифметической прогрессии равна $d$ , а знаменатель геометрической равен $q$ . Поскольку прогрессии непостоянны, $d⁄= 0$ и $q ⁄= 1$ . Возможны два случая:

1) Пусть $(an)$ — арифметическая прогрессия, а $(bn)$ — геометрическая. Тогда по условию получаем

3 a+ d= 2aq,a+ 3d= 8aq

d= a(2q− 1)

3d= a(8q3− 1)= d(4q2+ 2q+1)

2q2+q − 1= 0

q = 1 или q = −1 2

Если $q = 1∕2$ , то $d =a(2q− 1)= 0$ , что по условию невозможно.

Если $q = −1$ , то $d= −3a$ и $a3 :b3 = aa+q2d2-=− 5.$

2) Пусть теперь $(an)$ — геометрическая, а $(bn)$ — арифметическая прогрессия. Тогда

2(a+ d)= aq,8(a +3d)= aq3

2d= a(q− 2)

24d= a(q3− 8)= 2d (q2+ 2q+4)

2 q + 2q − 8= 0

q = 2 или q = −4

В первом случае снова $d= 0$ , что противоречит условию, а во втором $q = −4,d= −3a$ и $a3 :b3 = aa+q22d-=− 156 .$

Ответ:

$− 5$ или $− 16 5$

Ошибка.
Попробуйте повторить позже

Задача 3#47913

Внутри треугольника $ABC$ взята такая точка $D,$ что $BD = CD,∠BDC = 120∘.$ Вне треугольника $ABC$ взята такая точка $E,$ что $∘ AE = CE,∠AEC = 60$ и точки $B$ и $E$ находятся в разных полуплоскостях относительно $AC.$ Докажите, что $∘ ∠AFD = 90 ,$ где $F$ — середина отрезка $BE.$

Источники: ММО-2017, 11.4, автор - О.Н. Косухин, (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Нам нужно доказать, что угол равен 90 градусов. Наверное, мы понимаем, что углы считать тут совсем никак не выйдет. У нас есть какая-то непонятная точка D и не менее понятная точка E, и всё это завязано ещё с F. Жуть... Поэтому подумаем, как это можно доказать с помощью векторов. О каком тогда преобразовании плоскости можно вспомнить?

Подсказка 2

Верно, можно попробовать вспомнить про поворот и к тому же ещё увеличивать длину вектора, потому что отрезки у нас, к сожалению, различные, а так мы решим эту проблему. То есть будем доказывать, что повернув DF против часовой на 90 градусов и увеличив его, мы получим AF. Давайте обратим внимание на то, что нам дали равнобедренные треугольники с хорошими углами. Что можно тогда отметить в них, учитывая данную середину F в треугольнике BEC?

Подсказка 3

Ага, можно отметить середины сторон BC и EC. Тогда у нас будут две средние линии в треугольнике BEC. Вернёмся к нашим искомым векторам. Они у нас снова немного плохие, потому что ни с чем не связаны на картинке. Как тогда можно попробовать их выразить?

Подсказка 4

Да, их можно выразить через сумму векторов по правилу треугольника - это сумма средней линии и серединного перпендикуляра. Осталось только вспомнить, что если повернуть сумму векторов на угол, а потом увеличить их - это будет тоже самое, если сначала один из векторов повернуть на угол и увеличить, а потом аналогично со вторым. Теперь можно в явном виде записать то, что нам надо доказать, и понять, во сколько раз мы увеличиваем отрезки, используя углы равнобедренных треугольников.

Показать доказательство

$PIC$

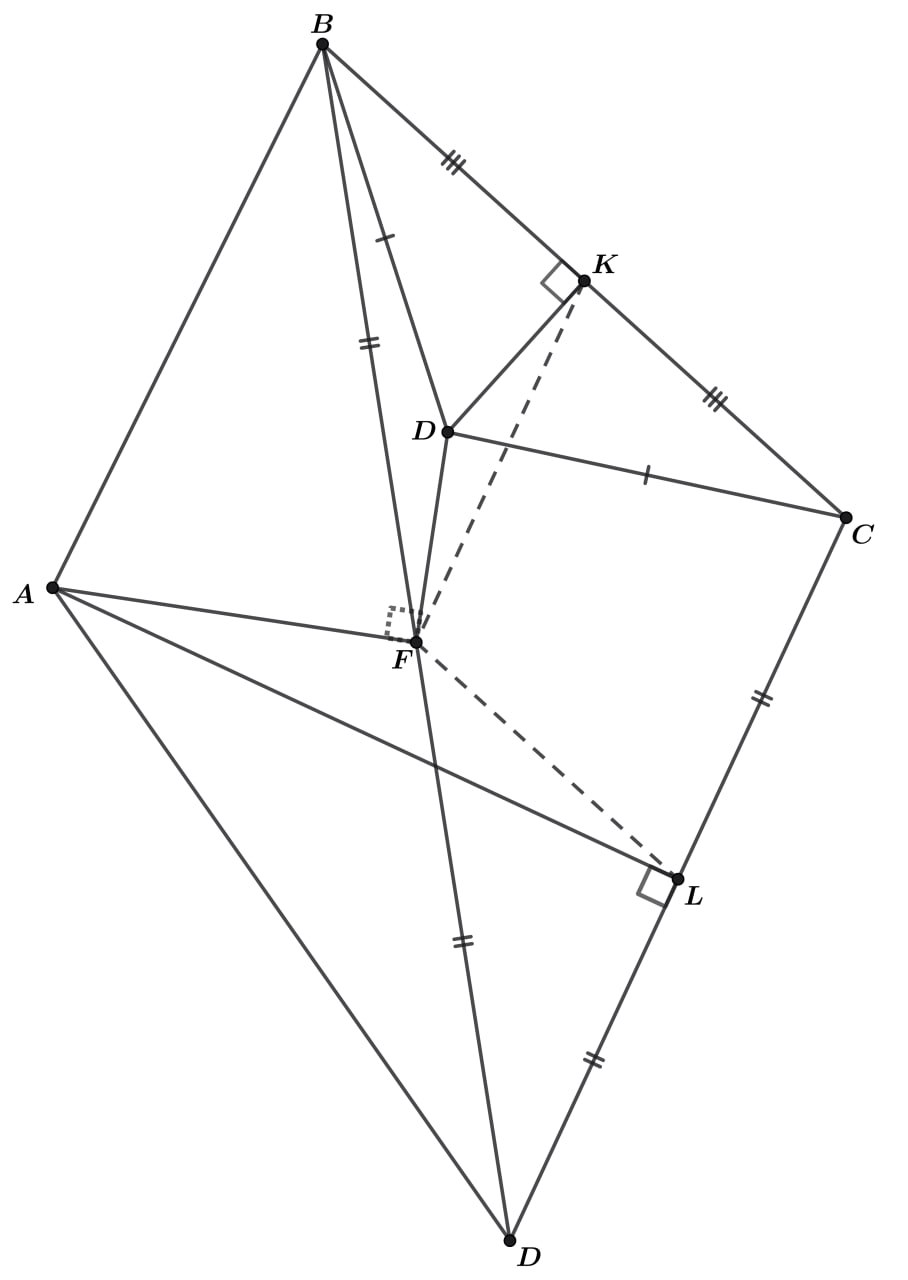
Пусть $K,L$ — середины $BC,CE$ соответственно. Отсюда $FL$ и $FK$ — средние линии $△EBC.$ Тогда выполнены равенства $−→ −−→ FL= BK$ и $−F−→K = −L→C.$ Пусть $Φ$ — преобразование на векторах, которое поворачивает вектор на $90∘$ против часовой стрелки, а затем увеличивает в $√3-$ раз. Тогда выполнено

Φ(−D−→K )= −−C→K =−L→F

Φ(−K−→F )=Φ (−C→L )=−A→L

Так как для поворотной гомотетии верно $−→ −→ Φ(−→a + b)= Φ(−→a)+ Φ(b),$ то

Φ(−−D→F )=Φ (−D−→K + −K−→F )= −→LF + −A→L =−A→F

Откуда и следует нужная перпендикулярность.

Ошибка.
Попробуйте повторить позже

Задача 4#77819

В шахматном турнире каждый участник встретился с каждым один раз. В каждом туре каждый участник проводил по одной встрече. Не меньше чем в половине всех встреч оба участника были земляками (из одного города). Докажите, что в каждом туре была хотя бы одна встреча между земляками.

Подсказки к задаче

Подсказка 1

Попробуем пойти от противного. Тогда в каком-то из туров игры между земляками не было. А что можно сказать о земляках конкретного участника?

Подсказка 2

В данном туре все участники разбиваются на пары, в каждой из которых двое не земляки. Тогда у любого конкретного участника из каждой пары не более одного земляка. Как тогда соотносятся земляки этого участника и общее число участников?

Подсказка 3

Верно! Поскольку в паре с данным участником был не его земляк, то земляков строго меньше половины всех участников. Тогда каждый сыграл с неземляками игр больше, чем с земляками. Какой вывод можно сделать?

Показать доказательство

Предположим, что в каком-то туре не было игры между земляками. Тогда участники разбиваются на пары людей из разных городов. Рассмотрим произвольного участника. В каждой паре есть не более одного его земляка, также второй участник из его пары не является его земляком. Но тогда всего земляков у него меньше половины из всех участников. Значит, каждый участник сыграл больше игр с неземляками, чем с земляками, и в сумме игр между земляками было меньше половины. Противоречие.

Ошибка.
Попробуйте повторить позже

Задача 5#78816

Квадратный трехчлен $x2+ bx+ c$ имеет два действительных корня. Каждый из трех его коэффициентов (включая коэффициент при $x2$ ) увеличили на $1.$ Могло ли оказаться, что оба корня трехчлена также увеличились на $1?$

Подсказки к задаче

Подсказка 1

В условии от нас хотят поработать с корнями и с коэффициентами квадратного трёхчлена. Какой теоремой хочется здесь воспользоваться?

Подсказка 2

Теорема Виета! Запишите её и воспользуйтесь условием.

Показать ответ и решение

Пусть $x ,x 1 2$ —корни уравнения $x2+ bx +c= 0.$ Тогда по теореме Виета

x1+ x2 = −b (1)

x1x2 =c (2)

Предположим, что утверждение задачи верно, тогда

x + 1+x + 1= − b+-1 (3) 1 2 2

c+-1 (x1+1)(x2+1)= 2 (4)

Подставим $(1)$ в $(3)$ и найдем $b= 5.$

Подставим $(1)$ и $(2)$ в $(4)$ и найдем $c= 9.$

Стало быть, искомый квадратный трехчлен, если он существует, имеет вид $2 x + 5x +9.$ Однако же дискриминант такого трехчлена отрицателен, а по условию он имеет два действительных корня. Значит, описанная в задаче ситуация невозможна.