ММО 2013
Ошибка.
Попробуйте повторить позже
Дан такой выпуклый четырехугольник что
и
Точки
и
— середины отрезков
и
соответственно. Перпендикуляр, проведенный из точки
к прямой
пересекается с перпендикуляром, проведенным из точки
к
прямой
в точке
Докажите, что прямые
и
перпендикулярны.
Подсказка 1
Для начала введём обозначения. S — основание перпендикуляра из А на BC, P — основание перпендикуляра из С на AD. Что мы имеем. ∠ASC = ∠APC = 90°. Какой тогда вывод можно сделать?
Подсказка 2
Верно! A,S,C,P лежат на окружности с диаметром AC. Что же можно сказать про центр этой окружности?
Подсказка 3
Это точка M — середина диаметра. Самостоятельно докажите, что BM — перпендикуляр к AC. Аналогично докажите, что BSMA, CMPD — вписанный.
Подсказка 4
Хотим доказать перпендикулярность прямых, у нас есть много окружностей с общими точками. На что же это намекает?
Подсказка 5
Именно! На радикальные оси и центры окружностей. Самостоятельно докажите, что H — радикальный центр трёх найденных окружностей. Также M — общая точка окружностей BSMA и DPMC. Какой вывод можно сделать?
Подсказка 6
HM — рад. ось BSMA и CMPD, осталось доказать, что KL — линия центров. Успехов!
Обозначим основание перпендикуляра, опущенного из точки на
через
а основание перпендикуляра, опущенного из точки
на
— через
Точки и
равноудалены от концов отрезка
значит
— серединный перпендикуляр к
Заметим, что точки
и
лежат на окружности с диаметром
точки
и
— на окружности с диаметром
а точки
и
— на окружности с
диаметром
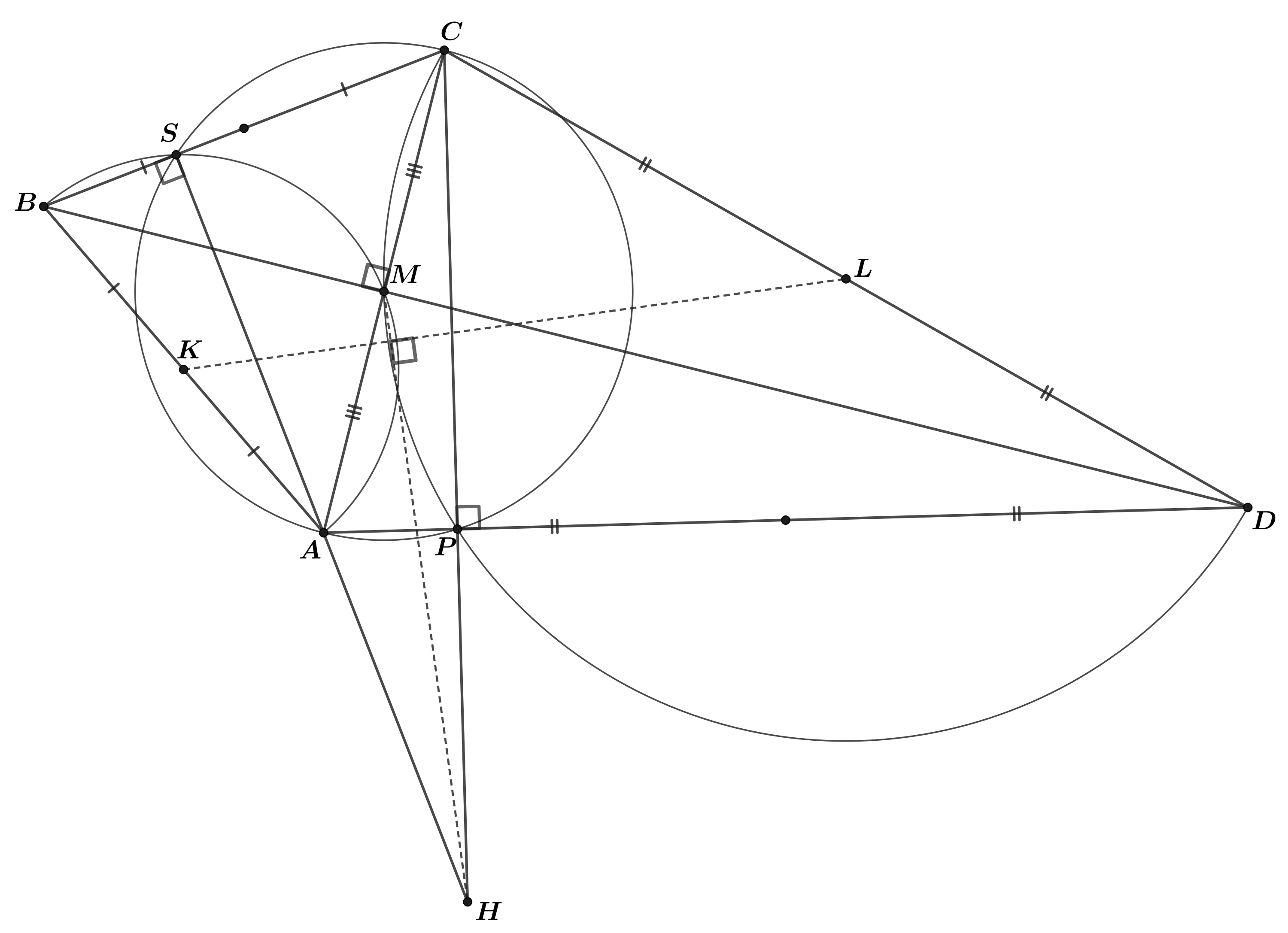
Прямая является радикальной осью окружностей
и
а прямая
— радикальной осью окружностей
и
Поэтому точка
пересечения этих прямых — радикальный центр трёх указанных окружностей.
Следовательно,
— радикальная ось окружностей
и
и, значит, перпендикулярна их линии центров
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




