ММО 2011
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Что больше: или
Подсказка 1
Неравенства a > b и a - b > 0 эквивалентны. Попробуем вместо сравнения исходных чисел сравнить их разность с нулем. Как можно преобразовать разность, чтобы было удобно ее оценивать?
Подсказка 2
Конечно! Перегруппируем слагаемые так, чтобы получилась разность двух скобок, внутри каждой у степеней одинаковое основание, а затем вынесем общий множитель. Как теперь сравнить числа?
Подсказка 3
Верно! Используем, что 2011 > 2009 и докажем, что в разности какое-то из чисел больше.
Запишем разность двух чисел, которые хотим сравнить, и преобразуем её:
Заметим, что и
Следовательно, уменьшаемое больше вычитаемого, то есть разность
положительна. Значит, первое число больше, будет знак
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике на основании
взята точка
а на боковой стороне
— точки
и
причем
и отрезок
параллелен стороне
Докажите, что
Источники:
Подсказка 1
Соберите информацию про рисунок, поищите ещë какие-то равнобедренные треугольники, кроме ABC.
Подсказка 2
Вообще требуемое неравенство должно получиться из неравенства треугольника. Чтобы понять, из какого именно, рассмотрите среднюю линию треугольника EAD.
Первое решение.
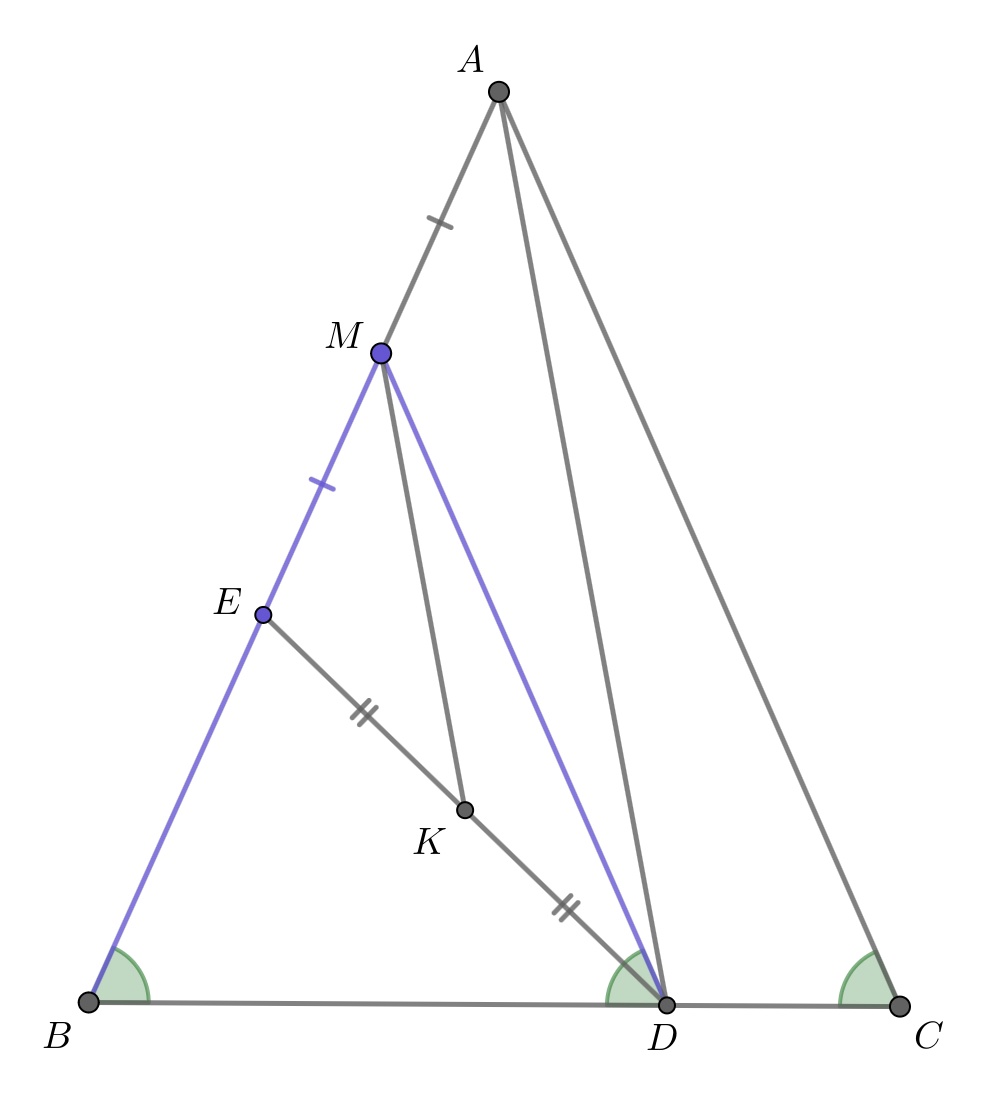
Так как то
и
Обозначим через
середину отрезка
Тогда
—
средняя линия в треугольнике
и
По неравенству треугольника:
Второе решение.
поскольку
поэтому треугольник
тоже равнобедренный и
Но
как медиана в треугольнике
Ошибка.
Попробуйте повторить позже
В треугольнике проведены биссектрисы
и
Известно, что центр описанной окружности треугольника
лежит на
прямой
Найдите угол
треугольника.
Подсказка 1
Попробуйте понять, что такое описанная окружность треугольника BB₁C₁ такая, что её центр лежит на прямой AC.
Подсказка 2
На самом деле важно, что эта окружность проходит через точки B, B₁, и её центр лежит на AC. Что же это за окружность?
Подсказка 3
Правильно! Это окружность Аполлония для точек A и C с коэффициентом AB/BC. Что тогда можно сказать про прямую C₁B₁?
Подсказка 4
Ага! Она является биссектрисой угла CC₁A! Теперь посмотрите внимательно на треугольник CBC₁ и поймите, чем для него является точка B₁.
Подсказка 5
Она является центром вневписанной окружности, которая лежит напротив вершины B. Осталось только посчитать углы при вершине С.
Рассмотрим окружность Аполлония для точек и
и коэффициентом
Она проходит через точки
и
и её центр лежит
на прямой
а значит, она совпадает с описанной окружностью треугольника
Поэтому
а значит,
— биссектриса угла
Следовательно,
— центр вневписанной окружности треугольника
то есть
— внешняя
биссектриса угла
То есть угол
равен
![]()

