ММО до 2010
Ошибка.
Попробуйте повторить позже
Подсказка 1, пункт (a)
На самом деле достаточно построить отрезок длины 1(иными словами, восстановить масштаб), ведь касательная имеет угловой коэффициент, равный cos(x) для заданной точки x. А как можно построить отрезок длины 1?
Подсказка 2, пункт (а)
Если удастся отметить точку π/2 на оси oX, то задача будет решена, ведь перпендикуляр к этой оси, проходящий через эту точку, пересекает график синуса в точке (π/2,1), и отрезок между точками пересечения единичный. А как построить эту точку?
Подсказка 3, пункт (а)
Конечно! Используем свойство sin(a) = sin(π-a)! Тогда отрезок между точками (a, sin(a)) и (a, sin(π-a)) параллелен оси oX. А что хорошего можно сказать о перпендикуляре к этому отрезку?
Подсказка 1, пункт (b)
Попробуем построить отрезок, равный синусу какого-нибудь угла? и этот угол так, чтобы они оказались элементами одного прямоугольного треугольника. Как этого можно добиться?
Подсказка 2, пункт (b)
Точно! Выберем на оси oX некоторые a и b и построим отрезок длины sin(a) + sin(b). Легко построить и отрезок длины sin((a+b)/2). А можно ли построить отрезок длины, равной синусу полуразности?
Подсказка 3, пункт (b)
Его можно построить с помощью простых построений середин, но тогда не получится прийти к отрезку длины 1, поэтому нужно найти прямоугольный треугольник. Для этого его нужно построить! Пусть его прямой угол будет в одном конце отрезка длины sin(a) + sin(b) (и его первая вершина соответственно), а вторая — в другом конце этого отрезка. А как получить третью вершину?
Подсказка 4, пункт (b)
Верно! Надо использовать построенный ранее sin((a+b)/2)! Строим окружность радиуса 2sin((a+b)/2) с центром во второй вершине предполагаемого треугольника! Пересечение построенного ранее перпендикуляра к одному из концов отрезка длины sin(a) + sin(b) и этой окружности будет третьей точкой! Чему тогда равен угол этого треугольника при втором конце отрезка длины sin(a)+sin(b)?
Подсказка 5, пункт (b)
Точно! Он равен (a-b)/2! Как уже было отмечено, построить sin((a-b)/2) нетрудно! А как теперь его поместить в наш треугольник, чтобы в нем появился отрезок длины 1?
Касательная к графику функции где
проведённая в заданной его точке
имеет угловой коэффициент, т.е.
тангенс угла наклона к оси
равный
и для её построения при помощи циркуля и линейки достаточно построить отрезок
длины
Действительно, имея отрезки
и
можно построить отрезок
(при помощи тригонометрического
круга), а значит, и угол, тангенс которого равен
Покажем, как построить отрезок длины
(т.е. восстановить
масштаб).
(a) Из точки где
лежащей на графике функции, опустим перпендикуляр на ось
(рис. слева). Так как
то этот перпендикуляр пересечёт график функции
в точке
Через середину отрезка
проведём прямую, перпендикулярную оси
Она пересечёт график в точке
Отрезок этой прямой от оси
до графика
функции
имеет длину
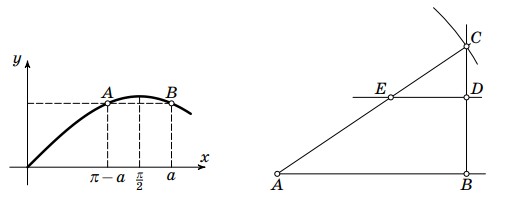
(b) Здесь несколько труднее построить отрезок единичной длины. Остальные построения будут такими же.
Пусть и
— произвольные точки на оси
удовлетворяющие условию
Построим отрезок
длины
Через точку
проведём луч
перпендикулярный отрезку
Окружность с центром в точке
и радиусом
пересекает луч
в точке
(рис. справа). Так как
то
На отрезке
отметим точку
такую, что
Через точку
проведём прямую, параллельную отрезку
Эта прямая пересечёт отрезок
в точке
Длина
отрезка
равна
так как
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




