ММО до 2010
Ошибка.
Попробуйте повторить позже
Найти геометрическое место середин отрезков с концами на двух различных непересекающихся окружностях, лежащих одна вне другой.
Подсказка 1
Пусть S₁ и S₂ — данные окружности, O₁ и O₂ — их центры. Может, попробуем параллельно перенести одну на другую?
Подсказка 2
Давайте считать, что R₁ ≤ R₂, параллельно перенесем вторую внутрь первой при помощи вектора (O₂O₁). Обозначим полученную окружности за S₂'. Пусть A₁ — точка окружности S₁, A₂ и A₂' — точки окружностей S₂ и S₂', соответствующие друг другу.
Подсказка 3
Пусть M — середина отрезка A₁A₂, M' — середина отрезка A₁A₂', тогда что можно сказать про вектор (M'M)?
Подсказка 4
В силу параллельного переноса, (M'M) = 1/2 * (O₁O₂). Какой случай тогда можно рассмотреть?
Подсказка 5
Далее будем рассматривать две концентрические окружности, ведь можно сдвинуть полученное ГМТ на данный вектор.
Подсказка 6
Пусть O — их центр, радиусы — R, r (R > r). Пусть точка А перемещается по меньшей окружности, В — по большей, рассмотрим середину этого отрезка.
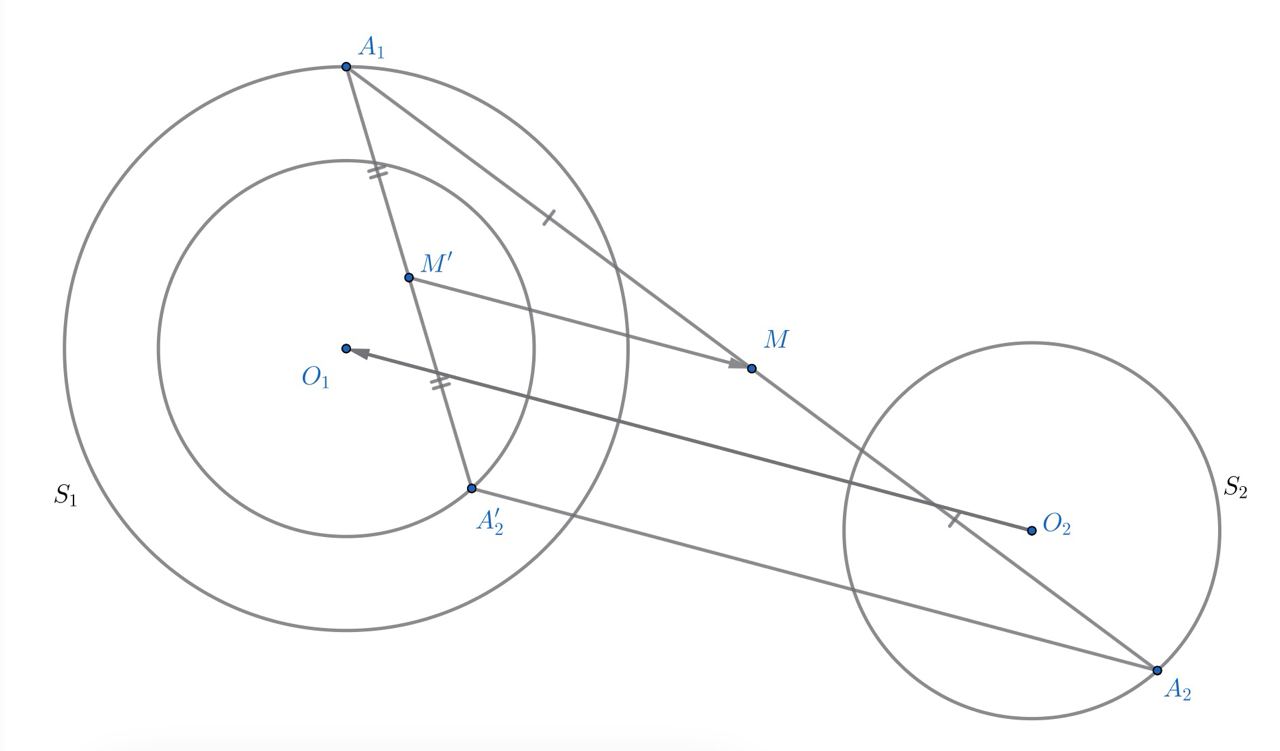
Пусть и
— данные окружности,
и
— их центры. Рассмотрим окружность
которая получается из
окружности
параллельным переносом на вектор
центр этой окружности совпадает с центром окружности
Пусть
— точка окружности
и
— точки окружностей
и
соответствующие друг другу. Если
— середина отрезка
а
— середина отрезка
то
Поэтому можно рассмотреть
случай, когда даны две концентрические окружности, потому что полученное ГМТ можно сдвинуть на вектор
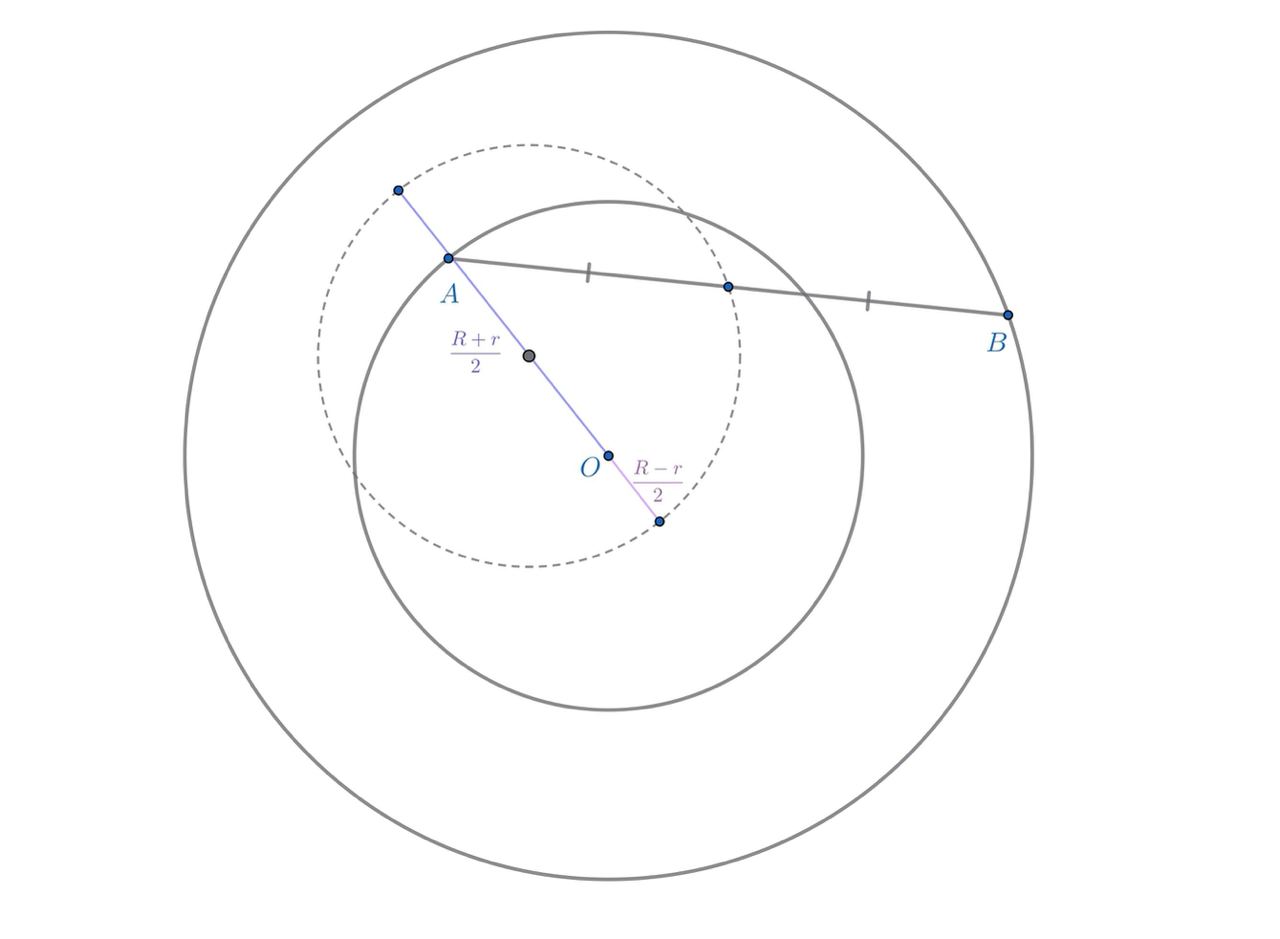
Пусть — общий центр двух окружностей радиусом
и
причём
Фиксируем на окружности радиуса
точку
и
рассмотрим середины всех отрезков
где точка
перемещается по окружности радиуса
Они образуют окружность
(в этом можно убедиться, если сделать гомотетию в
с коэффициентом
тогда все середины попадут на большую
окружность), причём её самая близкая к
точка находится на расстоянии
а самая далёкая — на расстоянии
Если
точка
будет двигаться по всей окружности, то мы получим кольцо с внутренним радиусом
и внешним радиусом
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




