Тема ПитерГор - задачи по годам

ПитерГор 2020

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела питергор - задачи по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68468

В неравнобедренном треугольнике $ABC$ проведена биссектриса $BB . 1$ Точка $I$ — центр вписанной окружности треугольника $ABC.$ Серединный перпендикуляр к отрезку $AC$ пересекает окружность, описанную около треугольника $AIC,$ в точках $D$ и $E.$ Точка $F$ на отрезке $B1C$ выбрана так, что $AB1 =CF.$ Докажите, что точки $B,D, E$ и $F$ лежат на одной окружности.

Подсказки к задаче

Подсказка 1

У нас есть треугольник AIC и его описанная окружность. Может, мы знаем что-то хорошее про ее центр?

Подсказка 2

По лемме о трезубце, это середина дуги AC! Обозначим ее за O. Кроме того, он лежит на отрезке ED, т.к. это серединный перпендикуляр к AC. Как можно теперь связать точки E и D так, чтобы можно было что-то сделать с точкой F похожим образом?

Подсказка 3

Например, можно сказать, что E и D симметричны относительно прямой, перпендикулярной ED и проходящей через O) Давайте также отразим F относительно этой прямой, и получим точку F'. Что мы получили?

Подсказка 4

Мы получили, что есть DEFF' - вписанная равнобокая трапеция. Мы хотим доказать, что E, D, B, F на одной окружности, а уже есть DEFF'..Как можно переформулировать теперь задачу?

Подсказка 5

Можно теперь доказывать, что точки F', D, B и E лежат на одной окружности) Для этого попробуйте доказать, что O - центр окружности B₁FF'! Это можно сделать с помощью симметрии, чтобы доказать, что O лежит на B₁F') А дальше как действовать?

Подсказка 6

А дальше можно воспользоваться подобием треугольников OAB и OAB₁ и записать отношения сторон) После с помощью предыдущей подсказки можно по-другому выразить это равенство отношений, и получится требуемое условие для того, чтобы F', D, B и E лежали на одной окружности)

Показать доказательство

$PIC$

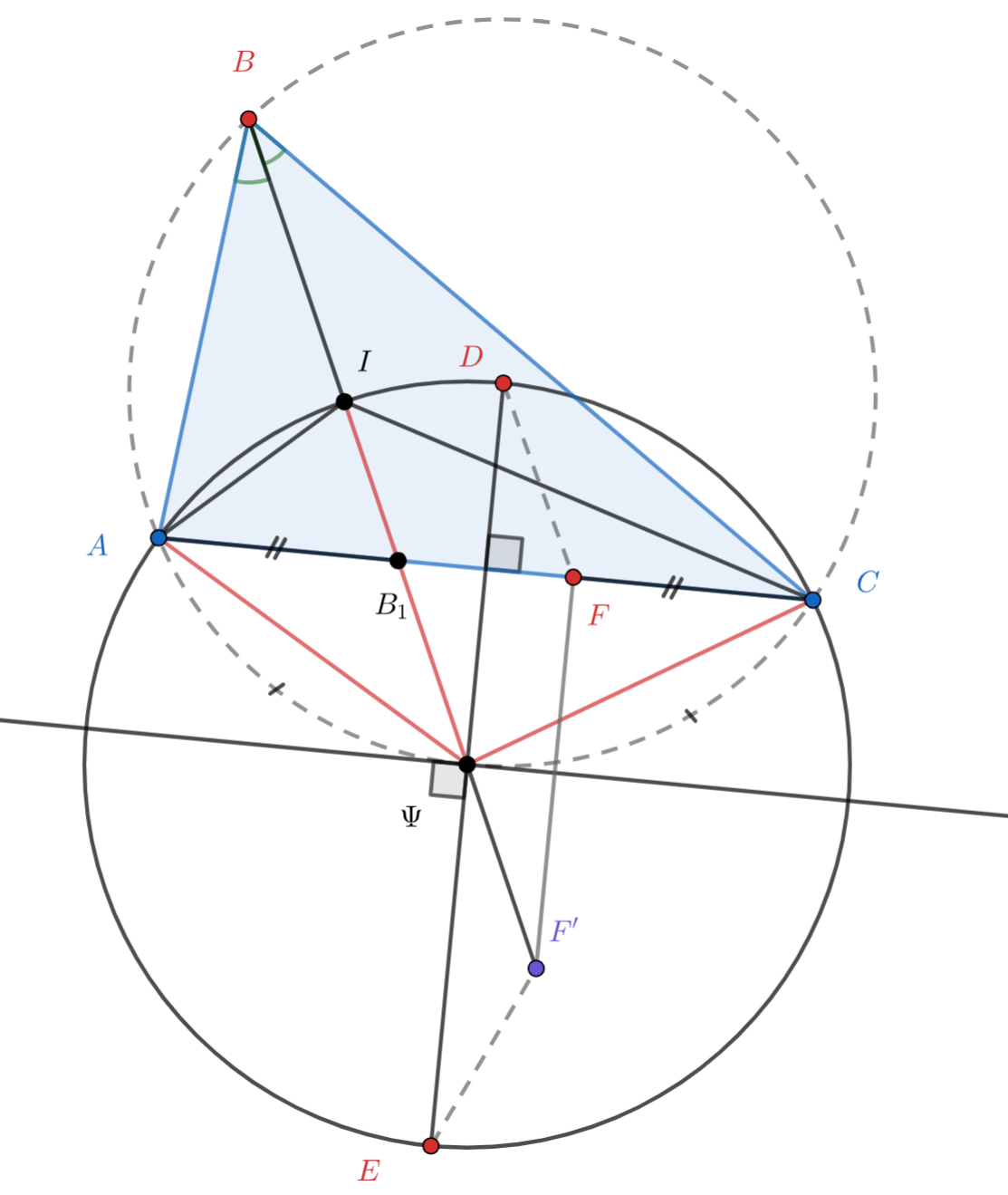
Обозначим через $Ψ$ середину дуги описанной окружности треугольника $ABC$ , не содержащей точку $B$ . Тогда $Ψ$ лежит на прямой $BB1$ . Кроме того, по лемме о трезубце точка $Ψ$ равноудалена от точек $I, A$ и $C$ , поэтому $Ψ$ является центром описанной окружности треугольника $AIC$ и $Ψ$ лежит на отрезке $ED$ . Пусть точка $F′$ симметрична точке $F$ относительно серединного перпендикуляра к $DE$ . Очевидно, $DEF ′F$ — равнобедренная трапеция, значит, $D, E, F, F′$ лежат на одной окружности.

Докажем, что точка $B$ лежит на этой же окружности. Заметим, что точка $F′$ лежит на $BB1$ , поскольку $Ψ$ равноудалена от точек $B1, F, F′$ и $∠F′F B1 = 90∘$ , т.е. $B1F′$ — диаметр окружности с центром $Ψ$ и радиусом $ΨF$ . Из подобия треугольников $AΨB1$ и $BΨA$ следует, что $ΨB1⋅ΨB = ΨA2$ , что равносильно равенству

ΨF′⋅ΨB = ΨD ⋅ΨE.

Из последнего равенства следует, что точки $F′, B, D, E$ лежат на одной окружности.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68469

Точка $I a$ — центр вневписанной окружности треугольника $ABC,$ касающейся стороны $BC$ в точке $X,$ а точка $A′$ диаметрально противоположна точке $A$ на описанной окружности этого треугольника. На отрезках $′ ′ IAX,BA ,CA$ выбраны точки $Y,Z,T$ соответственно таким образом, что $IAY = BZ = CT =r,$ где r — радиус вписанной окружности треугольника $ABC.$ Докажите, что точки $X,Y,Z,T$ лежат на одной окружности.

Подсказки к задаче

Подсказка 1

У нас в условии есть центры вписанной и вневписанной окружностей - попробуем посчитать какие-то углы, найти равные…хочется еще равные отрезки как-то использовать, не так ли? Еще заметим, что точки Z, T у нас практически одинаковы по построению, поэтому будет досрочно сделать выводы для одной из них, а потом произнести волшебное «аналогично». Не понятно, как подобраться к углам требуемого «вписанного» четырехугольника, поэтому попробуем доказать, что серединные перпендикуляры к его стороны пересекаются в одной точке.

Подсказка 2

С помощью подсказки 1, учитывая, что угол АВА´ прямой, приходим к тому, что ZBIaY равнобедренная трапеция! Что мы тогда может сказать о серединной перпендикуляре к ZY? А к BIa? Серединный перпендикуляр к последнему отрезку несложно найти с помощью известной леммы, которая ищет такую точку W, что WB = WIa. Аналогичные действия проделывает и с точкой T)

Подсказка 3

Серединные перпендикуляры к ZY и YT проходят через середину дуги BC окружности (ABC) по лемме о Трезубце и в силу того, что эти серединные перпендикуляры совпадают с серединными перпендикулярами к BIa и CIa. Осталось лишь доказать, что серединный перпендикуляр к XY проходит через эту же точку.

Подсказка 4

Для этого отложим на продолжении отрезка XIa за Х такую точку I’, что XI’ = r и подумаем о треугольнике IaI’I.

Показать доказательство

$PIC$

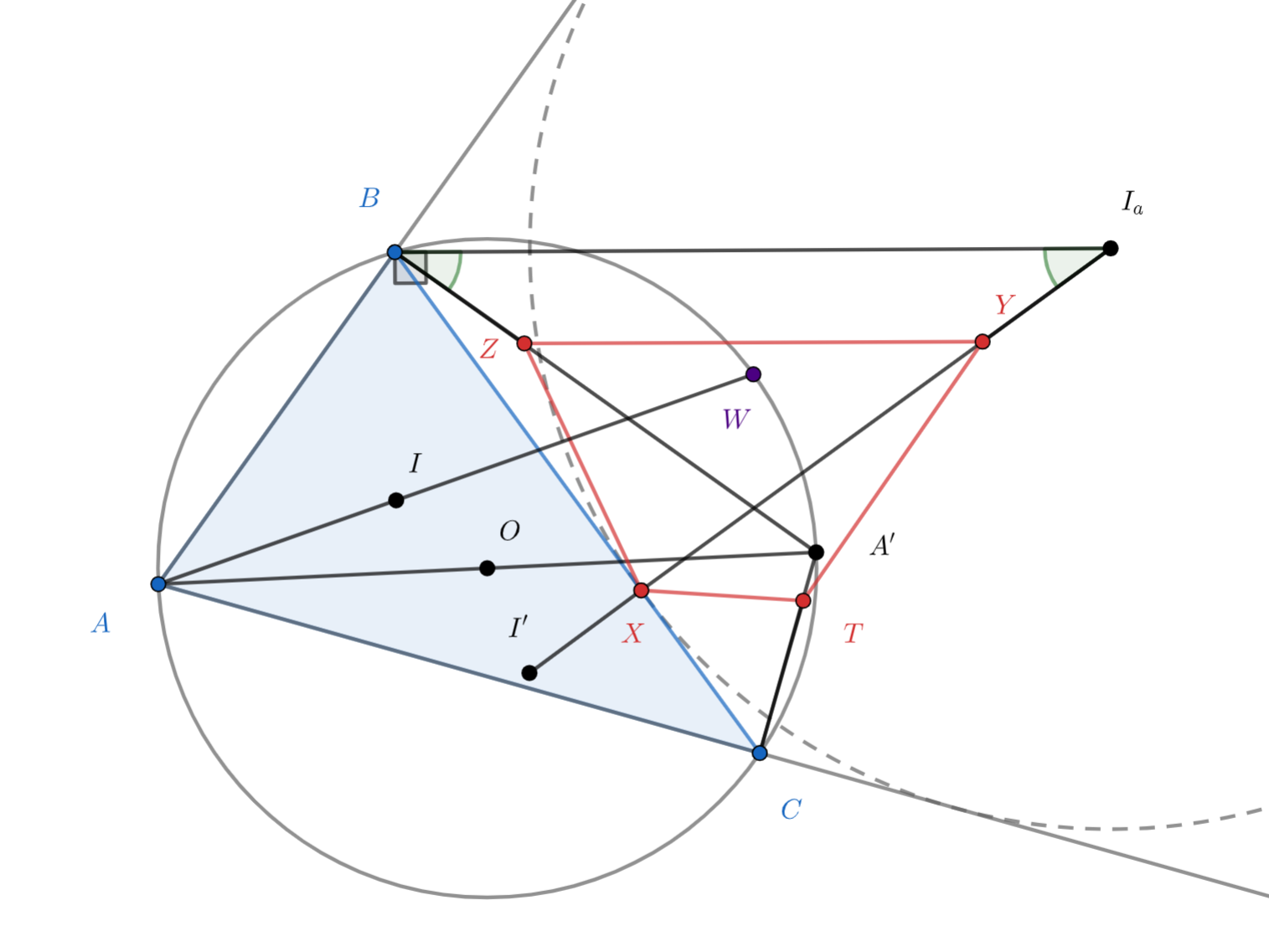
Из условия сразу следует, что $∠ABZ = 90∘$ . Кроме этого, если $I$ — центр вписанной окружности, то $∠IBIa = 90∘$ . Из этих равенств сразу следует, что $∠ZBIa = ∠ABI = ∠AB2C$ . Поскольку прямая $BIa$ — внешняя биссектриса угла $ABC$ , угол $CBIa = 90∘− ∠A2BC$ , и поэтому

∠YIaB = ∠XIaB = ∠ABC-. 2

Таким образом, $BZ =IaY$ и $∠ZBIa = ∠YIaB$ . Это значит, что четырехугольник $BIaYZ$ — равнобедренная трапеция. Поэтому серединный перпендикуляр к отрезку $YZ$ совпадает с серединным перпендикуляром к отрезку $BIa$ . Последний по лемме о трезубце проходит через середину $W$ дуги $BC$ описанной окружности треугольника. Аналогично, через $W$ проходит и серединный перпендикуляр к отрезку $YT.$

Осталось понять, почему через $W$ проходит серединный перпендикуляр к отрезку $XY$ . Отметим на продолжении отрезка $IaX$ за точку $X$ такую точку $I′$ , для которой $XI ′= r$ . Иными словами, $II′Ia$ — прямоугольный треугольник с прямым углом при вершине $I′$ . По уже упоминавшейся лемме о трезубце, точка $W$ — середина его гипотенузы $1Ia$ . Следовательно, она лежит на серединном перпендикуляре $I′I a$ совпадающем с серединным перпендикуляром к отрезку $XY.$

Ошибка.
Попробуйте повторить позже

Задача 3#69818

Близорукая ладья бьёт все клетки своей строки и своего столбца, до которых можно дойти не более чем за $60$ шагов, шагая из клетки в соседнюю по стороне. Какое наибольшее число не бьющих друг друга близоруких ладей можно расставить в квадрате $100× 100?$

Источники: СПбГОР - 2020, 11.2(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

В задачах на ходы необычных фигур полезно бывает выделить области, в которых мы точно сможем оценить количество фигур. Какие несложные фигуры для разбиения можно выбрать?

Подсказка 2

Обратим внимание на полоски из клеток. Какого размера можно их взять для разбиения, чтобы точно оценить количество ладей в них?

Подсказка 3

Полоски размером 1*61! Попробуем симметрично разбить таблицу так, чтобы использовать достаточно большое количество таких полосок. Оценка может помочь построить пример)

Показать ответ и решение

Оценка. В задачах на ходы необычных фигур полезно бывает выделить области, в которых мы точно сможем оценить количество фигур. Тут оценка на самом деле следует более-менее из попытки построить пример. Реализуем здесь эту идею. Разобьём квадрат $100 ×100$ на центральный квадрат $22× 22$ и $4⋅39 =156$ прямоугольников $1× 61.$ В каждый прямоугольник разбиения и в каждую горизонталь квадрата $22×22$ можно поставить не более одной ладьи, поэтому ладей не более $178.$

$PIC$

Пример. Поставим ладьи на клетки главной диагонали и двух параллельных ей диагоналей, состоящих из $39$ клеток. При такой расстановке между ладьями, расположенными в одном столбце и одной строке, находится ровно $60$ пустых клеток, поэтому никакие две ладьи не бьют друг друга.

$PIC$

Ответ:

$178$

Ошибка.
Попробуйте повторить позже

Задача 4#71929

Натуральное число назовём $гипотенузным,$ если оно может быть представлено в виде суммы двух квадратов целых неотрицательных чисел. Докажите, что любое натуральное число, большее $10,$ является разностью двух гипотенузных.

Источники: СпбОШ - 2020, задача 11.1(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала научимся представлять нечетные числа. Пусть есть число 2k + 1. Где такое выражение встречается в контексте квадратов?

Подсказка 2

Верно! Если прибавить к 2k + 1 число k², то получим (k+1)². Попробуйте что-то похожее придумать для четных.

Показать доказательство

Для нечётных чисел подойдет представление

( 2 2) (2 2) 2k+ 1= (k +1) +0 − k +0

а для чётных

( 2 2) ( 2 2) 2k = (k+ 1) + 0 − k +1 .

Ошибка.
Попробуйте повторить позже

Задача 5#71930

В неравнобедренном треугольнике $ABC$ проведена биссектриса $BB . 1$ Точка $I$ — центр вписанной окружности треугольпика $ABC.$ Серединный перпендикуляр к отрезку $AC$ пересекает окружность, описанную около треугольника $AIC,$ в точках $D$ и $E.$ Точка $F$ на отрезке $B1C$ выбрана так, что $AB1 =CF.$ Докажите, что точки $B,D, E$ и $F$ лежат на одной окружности.

Источники: СпбОШ - 2020, задача 11.3(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Раз в задаче фигурирует окружность AIC, то было бы неплохо подумать про её центр. И про то, как он связан с описанной окружностью ABC. В этом вам поможет лемма о трезубце.

Подсказка 2

В конструкции с трезубцем есть довольно много равных углов, а значит, и подобных треугольников. Например, посмотрите на треугольники AMB₁ и BMA.

Подсказка 3

Проделайте некоторые трюки с подобием и равными отрезками. Запишите равенства подобия для треугольников из прошлой подсказки. Отрезок MA можно заменить на какой-то другой, равный ему и найти какие-то другие подобные треугольники.

Показать доказательство

Обозначим через $M$ середину дуги $AC$ описанной окружности треугольника $ABC,$ не содержащей точку $B.$ Тогда точка $M$ лежит на прямой $BB1$ и по лемме о трезубце точка $M$ равноудалена от точек $I,A$ и $C$ , поэтому $M$ лежит на отрезке $ED$ и является центром описанной окружности треугольника $AIC$ . Следовательно,

MA =MC =MD = ME

Первое решение.

$PIC$

Из подобия треугольников $AMB1$ и $BMA$ следует, что

MB1 ⋅MB = MA2 = MD2 = ME2

Тогда $MB1- MD- MD = MB$ и, значит, треугольники $MB1D$ и $MDB$ подобны. Следовательно,

∠EDF =∠MDF = ∠MDB1 =∠MBD

Аналогично $MB1-= ME-, ME MB$ и, значит, треугольники $MB E 1$ и $MEB$ подобны. Следовательно,

∠DEF =∠MEF = ∠MEB1 =∠MBE

Таким образом,

∠DBE =∠MBD + ∠MBE =∠EDF +∠DEF = 180∘− ∠DFE

Стало быть, точки $B,D,E$ и $F$ лежат на одной окружности.

Второе решение.

$PIC$

Пусть точка $F′$ симметрична $F$ относительно серединного перпендикуляра к $DE.$ Очевидно, $DEF ′F$ — равнобедренная трапеция, значит $D,E$ , $F ′,F$ лежат на одной окружности.

Докажем, что точка $B$ лежит на этой же окружности. Заметим, что точка $F′$ лежит на $BB1,$ поскольку $M$ равноудалена от точек $B1,F,F′$ и $∠F′F B1 = 90∘,$ т. е. $B1F′$ — диаметр окружности с центром $M$ и радиусом $MF.$ Из подобия треугольников $AMB1$ и $BMA$ следуег, что

$MB1 ⋅MB = MA2,$ что равносильно равенству $MF ′⋅MB = MD ⋅ME.$ Из последнего равенства следует, что точки $F ′,B,D,E$ лежат на одной окружности.

Ошибка.
Попробуйте повторить позже

Задача 6#71931

Сумму

2 2 ⋅5 2 ⋅5 ⋅...⋅2015 3⋅6 +3-⋅6-⋅9 +...+3-⋅6-⋅...⋅2019

записали в виде десятичной дроби. Найдите первую цифру после запятой.

Источники: СпбОШ - 2020, задача 11.4(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Попробуйте представить каждое слагаемое в виде разности так, чтобы большинство членов взаимно уничтожались. Для этого достаточно посмотреть на последние множители числителя и знаменателя.

Подсказка 2

Итак, вы получили разность 2/3 и какой-то большой дроби. Эту дробь хочется оценить. Глобальная идея такая: попробуйте рассмотреть ещё какие-то дроби, похожие на неё и оцените её снизу и сверху произведениями этих дробей (которые должны быть равны чему-то более-менее простому, то есть большинство множителей должно сократиться).

Подсказка 3

Пусть дробь, которую нужно оценить, равна C, а четыре другие — A, B, D, E. Подберите их так, что A < B < C < D < E и ABC < C³ < CDE.

Показать ответ и решение

Для начала упростим данную сумму. Каждое слагаемое запишем в виде разности

2⋅5⋅...⋅(3k− 1) 3⋅6⋅9⋅...⋅(3k+-3) =

= 2⋅5⋅...⋅(3k−-1)⋅(3k+-3)− 2⋅5⋅...⋅(3k−-1)⋅(3k+-2)= 3⋅6⋅9⋅...⋅(3k +3) 3⋅6⋅9⋅...⋅(3k+3)

= 2⋅5⋅...⋅(3k-− 1)− 2⋅5⋅...⋅(3k− 1)⋅(3k-+2) 3⋅6⋅9⋅...⋅3k 3⋅6⋅9⋅...⋅(3k+ 3)

Тогда вся сумма телескопически сократится до разности крайних слагаемых

2 2⋅5⋅...⋅2018 3 − 3⋅6⋅...⋅2019

Решение 1.

Оценим вычитаемое. Заведем переменные

A = 1⋅3⋅6⋅...⋅2016, B = 1⋅4⋅7⋅...⋅2017 21⋅⋅54⋅⋅87⋅⋅......⋅⋅22001178 23⋅5⋅6⋅⋅89⋅⋅.....⋅.2⋅2001189 C = 3-⋅6-⋅9-⋅...⋅2019, D = 4⋅7⋅10⋅...⋅2020 4⋅7⋅10-⋅...⋅2020- E = 5⋅8⋅11 ⋅...⋅2022

Мы хотим оценить величину числа $C.$

Поскольку $a−1 -a- a <a+1$ при натуральных $a,$ выполняются неравенства $A < B < C <D < E,$ откуда

ABC <C3 < CDE

Подставив в эти неравенства формулы для наших чисел и сократив дроби, получим

-1-- 3 -2-- 2019 <C < 2022

Тогда

1 ∘--1- ∘--2- 1 15-< 3 2019-<C < 3 2022-< 6

и значит,

1 < 2− 2⋅5⋅...⋅2018-< 3 2 3 3⋅6⋅...⋅2019 5

Таким образом, первая цифра после запятой исходного числа равна $5.$

Решение 2.

Оценим с двух сторон выражение

( )( ) ( ) C = 2⋅5⋅8⋅...⋅2018-= 1− 1 1 − 1 ... 1− --1- (∗) 3⋅6⋅9⋅...⋅2019 3 6 2019

Для этого заметим, что

k − 1 1 ( 1 )3 1 k --k- =1 −k < 1− 3k < 1− k+-1 = k-+1 (∗∗)

Действительно,

( ) 1− -1 3 =1− 1 + 1--−--1- 3k k 3k2 27k3

поэтому левое неравенство очевидно. Для проверки правого достаточно установить, что

-12-− -13-= 9k-− 13-<--1---= 1 −--1- 3k 27k 27k k(k+ 1) k k +1

последнее сразу видно после умножения на $27k3$ и раскрытия скобок.

Неравенства $(∗∗)$ позволяют оценить произведение $(∗)$ сверху и снизу. Действительно,

(( 1 )( 1) ( 1) ( -1-))3 1 2 3 673 -1- 1 −3 1− 6 1− 9 ... 1− 2019 < 2 ⋅3 ⋅4 ⋅...⋅674 = 674

поэтому

C <-3√1--< √31--= 1< 1 674 512 8 6

Аналогично

(( 1) ( 1)( -1) ( -1--))3 1 2 3 672- 1-- 1− 6 1− 9 1 −12 ... 1− 2019 > 2 ⋅3 ⋅4 ⋅...⋅673 = 673

Поэтому

C > 2 ⋅3√1-> 2 ⋅3√1--= 2 ⋅ 1=-2 >-1 3 673 3 729 3 9 27 15

Итак, $1-<C < 1 15 6$ и, значит, $1= 2− 1< 2 − C < 2− 1-= 3. 2 3 6 3 3 15 5$

Ответ:

первая цифра после запятой равна $5$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#71932

Высоты $BB 1$ и $CC 1$ остроугольного треугольника $ABC$ пересекаются в точке $H.$ Окружность с центром в точке $O b$ проходит через точки $A,C1$ и середину отрезка $BH.$ Окружность с центром в точке $Oc$ проходит через точки $A,B1$ и середину отрезка $CH.$ Докажите, что

BC B1Ob+ C1Oc >-4-

Источники: СпбОШ - 2020, задача 11.5(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Попробуйте поработать с правой частью неравенства. Оцените её какими-то отрезками, которые хорошо связаны с окружностями из условия.

Подсказка 2

Всё гениальное просто: BC < BH + CH. Осталось показать, что первый отрезок из левой части неравенство не меньше BH/4. Для второго отрезка и CH/4 будет аналогично.

Подсказка 3

На самом деле, в последнем нестрогом неравенстве нужно доказывать равенство. Попробуйте для этого рассмотреть точку, симметричную точке B относительно AC. Быть может, она какая-то особенная, связана с каким-нибудь объектом?

Показать доказательство

Прежде всего, обозначим середину отрезка $BH$ через $M,$ а окружность, проходящую через $A,C 1$ и $M,$ — через $ω.$

Поскольку $1 1 1 4BC < 4BH + 4CH,$ для решения задачи достаточно доказать неравенство $1 B1Ob ≥ 4BH$ (и, аналогично, $1 ) C1Oc ≥ 4CH .$

Это неравенство следует из удивительного факта: расстояние от точки $Ob$ до прямой $AC$ равно в точности $1 4BH.$ Докажем его двумя способами: в обоих мы обнаружим на окружности $w$ ещё одну точку.

Решеение 1.

Пусть точка $′ B$ симметрична вершине $B$ относительно прямой $AC.$ Проверим,

$PIC$

что она лежит на окружности $ω.$ Для этого достаточно проверить, что $BM ⋅BB′ = BC1 ⋅BA.$ В самом деле,

$BM ⋅BB′ = BM ⋅2BB1 =2BM ⋅BB1 = BH ⋅BB1 =BC1 ⋅BA,$ последнее равенство следует из вписанности четырехугольника $AB1HC1.$

Таким образом, центр $Ob$ окружности $w$ должен лежать на серединном перпендикуляре к её хорде $MB ′.$ Значит, расстояние от $Ob$ до $AC$ равно расстоянию между этим серединным перпендикуляром и прямой $AC,$ то есть между серединами отрезков $B′M$ и $B′B.$ Оно в два раза меньпе, чем расстояние от $M$ до $B,$ т. е. равно $1BH. 4$

Решение 2.

Отметим такую точку $A′,$ что $−−A→A′ = −−B→M.$ Пусть $∠BAC = α,$ тогда $∠C1AA ′ = ∠BAC +∠CAA ′ = α+ 90∘.$

С другой стороны, медиана $C M 1$ прямоугольного треугольника $BC H 1$ равна $BM,$ и $∠BC M = ∠C BM = 90∘ − α. 1 1$ 3начит, $∠MC A =90∘+ α. 1$ Итак, $∠MC A = 1$ $= ∠C AA ′ 1$ и $C M = BM = AA′. 1$ Следовательно, четырехугольник $MC AA ′ 1$ — равнобедренная трапеция, так что $A′$ лежит на окружности $AC M, 1$ т. е. на $ω.$

$PIC$

Поскольку центр $Ob$ лежит на серединном перпендикуляре к $AA′,$ расстояние от него до $AC$ равно $12AA ′ = 12BM = 14BH,$ что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 8#71933

Последовательность $(a ) n$ задана условиями

a1 = 1, a2 = 2 и an+2 = an(an+1 +1) при n ≥1.

Докажите, что $aa n$ делится на $(an)n$ при $n ≥100.$

Источники: СпбОШ - 2020, задача 11.6(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Будем исследовать степень вхождения простого p в элементы последовательности. Пусть k - первый номер, для которого a_k делится на p. Тогда что можно сказать про k+2-й член последовательности?

Подсказка 2

Степень вхождения p в него хотя бы на 1 больше, чем в a_k. Аналогично можно получить, что степень вхождения в (k+2n)-ый член последовательности, больше хотя бы на n. Нам нужно проверить, что для всех p a_m-ый член последовательности имеет степень вхождения p хотя бы в m раз больше, чем m-ый.

Подсказка 3

Заметим, что m и a_m одной чётности, тогда мы хотим понять, что (a_m - m) это достаточно много, чтобы степень вхождения p точно получилась большой.

Показать доказательство

Пусть простое число $p$ входит в $a n$ в $k$ -й степени. Докажем, что $a an$ делится на $pkn.$ Тогда утверждение задачи будет выполнено.

Пусть $ai$ — первое число в нашей последовательности, кратное $p.$ Если $p⁄= 2,$ то $i> 2$ и $ai = ai−2(ai−1+ 1).$ Следовательно,

ai−1 ≡ −1 (modp)

Заметим, что для $p= 2$ будет $i= 2,$ и выведенное сравнение тоже выполнено.

Итак, $ai−1 ≡ −1,ai ≡ 0,$ а тогда дальше в последовательности чередуются остатки $− 1$ и $0$ от деления на $p:$

a = a (a + 1)≡ −1 ⋅(0+ 1)=− 1 (modp) i+1 i−1 i ai+2 = ai(ai+1+ 1)≡ 0⋅(−1+ 1)=0 (modp) и т.д.

Более того, как видно из последнего вычисления, степени числа $p,$ на которые делятся члены последователыности, растут: если $ai$ делилось на $p,$ то $ai+2$ делится на $2 p$ и т. д. Отсюда следует, что если $an$ делится на $k p,$ то $an+2t$ делится на $k+t p .$ Кроме того, учтем, что числа $an$ и $n$ одинаковой четности, поскольку $a1 =1,$ $a2 = 2$ и остатки по модулю $2$ чередуются. Следовательно, $aan$ делится на $k+(a −n)∕2 p n .$ Остается заметить, что $n an > 2$ при $n≥ 5$ (это значит, что $an$ существенно крупнее $n$ ) и $k an ≥2 ,$ так как делится на $k p$ (это значит, что $an$ существенно крупнее $k$ ), поэтому $an− n >2kn$ , откуда следует требуемое.

Ошибка.
Попробуйте повторить позже

Задача 9#71934

$N$ олигархов построили себе страну с $N$ городами, каждый олигарх владеет ровно одним городом. Кроме того, каждый олигарх построил несколько дорог между городами: любая пара городов соединена максимум одной дорогой каждого из олигархов (между двумя городами может быть несколько дорог, принадлежащих разным олигархам). Суммарно было построено $d$ дорог. Некоторые олигархи хотели бы создать корпорацию, объединив свои города и дороги так, чтобы при этом из любого города корпорации можно было доехать до любого другого ее города по дорогам этой корпорации, возможно, заезжая по дороге в города других олигархов. Но оказалось, что никакая группа олигархов создать корпорацию не может! При каком наибольшем $d$ это возможно?

Источники: СпбОШ - 2020, задача 11.7(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1

Для начала построим пример. Попробуем выделить группу олигархов. Тогда пусть какой-то город окажется изолированным (ведь именно в таком несвязном графе больше всего рёбер).

Подсказка 2

Это позволяет прийти к конструкции, в которой олигархи занумерованы, и имеют дороги между городами олигархов с меньшим номером. Для оценки будем говорить, что дорога нравится олигарху, если она принадлежит этому олигарху или город на одном из концов дороги принадлежит этому олигарху.

Подсказка 3

Дорога не может нравиться олигархам на её концах, так что каждая дорога нравится ровно трём олигархам. Осталось показать, что одной и той же тройке не могут нравиться две дороги, и подсчитать комбинаторно оценку.

Показать ответ и решение

Пронумеруем олигархов и их города числами от $1$ до $N$ соответственно.

Пример.

Пусть дорога между городами $i$ и $j$ принадлежит олигарху под номером $k$ тогда и только тогда, когда $k > i,k> j.$ Тогда количество дорог равно

(N − 1)(N − 2) (N − 2)(N − 3) 2⋅1 -----2----- + -----2-----+ ...+ -2-= 1 ( 2 2 2 2 ) = 2 (N( − 1) − (N − 1)+(N − 2) − (N)− 2)+ ...+ 2 − 2 +1 − 1 = = 1 N(N-− 1)(2N-−-1)-− N-(N-−-1) = N-(N-−-1)(N-− 2) 2 6 2 6

Проверим, что этот пример удовлетворяет условию задачи. Предположим, что это не так и какая-то группа олигархов смогла создать корпорацию. Пусть $M$ — наибольший номер олигарха в этой корпорации. Тогда из города $M$ не выходит ни одной дороги, принадлежащей членам корпорации, что противоречит тому, что из этого города можно добраться до любого города корпорации.

Оценка 1.

Будем говорить, что дорога $нравится олигарху,$ если она принадлежит этому олигарху или город на одном из концов дороги принадлежит этому олигарху. Заметим, что из города не может выходить дорога, принадлежащая владельцу этого города, так как в этом случае владельцы городов, которые соединяет эта дорога, могут образовать корпорацию. Следовательно, любая дорога нравится ровно трём олигархам. Сопоставим каждой дороге тройку олигархов, которым она нравится.

Рассмотрим произвольную тройку олигархов $A,B$ и $C.$ Докажем, что эта тройка сопоставлена не более чем одной дороге.

Предположим, что это не так. Выбраниая тройка олигархов может быть сопоставлена всего трем дорогам (если таковые имеются): дороге $BC,$ принадлежащей олигарху $A,$ дороге $AC,$ принадлежащей $B,$ и дороге $AB,$ принадлежащей $C.$ Легко видеть, что каким бы двум из этих дорог ни была сопоставлена тройка $A,B,C,$ эта тройка олигархов сможет образовать корпорацию. Следовательно, каждая тройка олигархов сопоставлена не более одной дороге, т. е. дорог не более $C3N .$

Заметим, что в нашем примере любая тройка олигархов $i< j < k$ сопоставлена дороге $ij,$ принадлежащей олигарху $k,$ т. е. всего $C3N$ дорог, что дает комбинаторный способ подсчета количества дорог в примере.

_________________________________________________________________________________________________________________________________________________________________________________

Оценка 2.

Рассмотрим граф, в котором вершиины — это города, а ребра цвета $i$ — дороги, принадлежащие олигарху номер $i.$ Заметим, что если из графа, удовлетворяющего условию задачи, удалить часть вершин, выходящие из них ребра и все ребра, принадлежащие олигархам-владельцам удаляемых вершин, то для оставшегося графа условие задачи о невозможности построить корпорацию продолжит выполняться.

Докажем индукцией по $N,$ что если в графе $N$ вершин, то при удалении любой вершины, всех ее ребер и всех ребер соответствующего ей цвета суммарное количество ребер уменьшается не более чем на $(N−1)(2N−2).$

База $N = 2$ очевидна.

Переход. Пусть мы хотим удалить олигарха номер $N$ . Так как все $N$ олигархов не могут образовать корпорацию, граф на. ребрах всех цветов несвязен. Обозначим через $U$ компоненту связности, содержащую город олигарха номер $N$ , через $V$ — объединение всех остальных компонент связности, а через $u$ и $v$ — количество вершин в $U$ и $V$ соответственно. Тогда подграф $V$ содержит не более $v(v−1) 2$ ребер $N$ -го цвета. Далее, из вершины $N$ выходит не более $v(u− 1)$ ребер с цветами, соответствующими вершинам из $V.$ Наконец, применяя к графу $U$ индукционное предположение, получаем, что в графе $U$ имеется не более $(u−1)(u−2) 2$ ребер, имеющих цвет $N$ или выходящих из вершины $N.$ Следовательно, при удалешии вершины $N$ исчезнет не более

v(v− 1)+ v(u− 1)+(u−-1)(u−-2)= 2 (v+2u− 1)(v+ u− 2) (N − 1)(N − 2) = -------2--------= -----2-----

ребер.

Для доказательства оценки будем по одной удалять вершины, подсчитывая, сколько ребер при этом пропадает. Получается, что мы удалили не более $C2N−1+ C2N−2+ ...+ C22 = C3N$ ребер. Заметим, что если в нашем примере удалять олигархов в порядке убывания номеров, то при удалении олигарха номер $k$ будет пропадать в точности $(k−1)(k2−2)$ ребер. Следовательно, в любом графе ребер не больше, чем в построенном нами примере.

Ответ:

максимальное число дорог равно $N(N-−1)(N−2) 6$

Ошибка.
Попробуйте повторить позже

Задача 10#73686

В социальной сети у каждого пользователя не более десяти друзей (отношение “дружба” симметрично). Сеть связна: если, узнав интересную новость, пользователь начинает рассылать её своим друзьям, те своим и так далее, то в итоге новость узнают все пользователи. Докажите, что администрация сети может разбить пользователей на группы так, чтобы выполнялись следующие условия:

$1$ ) каждый состоит ровно в одной группе;

$2$ ) каждая группа связна в указанном выше смысле;

$3$ ) одна из групп содержит от $1$ до $100$ членов, а каждая из остальных от $100$ до $900$ членов.

Источники: СпбОШ - 2020, задача 10.6(см. www.pdmi.ras.ru)

Показать доказательство

Социальная сеть представляет собой граф, в котором люди - это вершины, а отношение “дружба” — ребра. Достаточно рассмотреть случай, когда этот граф является деревом. В требованиях условия задачи группу, в которой состоит от $1$ до $100$ членов, будем называть малой, а группу, где от $100$ до $900$ членов, — большой. Докажем утверждение задачи индукцией по числу пользователей сети. База индукции: $n ≤900.$ Если в сети не более $100$ пользователей, объявим их всех малой группой. Если в сети от $101$ до $900$ пользователей, назначим малой группой любого пользователя, соответствующего висячей вершине, а всех остальных запишем в большую группу.

Индукционный переход. Достаточно проверить, что если число пользователей больше $900,$ то можно подобрать большую группу, при удалении которой граф останется связным. Подвесим наше дерево и рассмотрим наиболее далекую от корня вершину $A$ (одну из вершин), у которой больше $900$ потомков. У каждого из сыновей вершины $A$ не более $900$ потомков, при этом количество сыновей — не более $9.$ Если у каждого из сыновей $A$ не более $99$ потомков, то в сумме у $A$ не более $9⋅99< 900$ потомков, что противоречит выбору вершины $A.$ Значит, один из сыновей $A$ имеет от $100$ до $900$ потомков, назначим его и его потомков большой группой.