ПитерГор 2016
Ошибка.
Попробуйте повторить позже
На стороне неравнобедренного треугольника
выбраны точки
и
так, что
и
Серединный
перпендикуляр к отрезку
пересекает биссектрису угла
в точке
(внутри треугольника). Докажите, что
Источники:
Подсказка 1
Кажется на рисунке не хватает какой-то важной точки. Нам даны биссектриса, возможно эта дополнительная точка как-то с ней связана... Хм, отметим центр вписанной окружности треугольника, возможно это нам поможет.
Подсказка 2
А теперь ещё один классический трюк. Давайте попробуем найти на рисунке равные треугольники... И правда, △ACI и △API равны между собой. Ой-ой-ой, так ведь это означает, что IP = IC. Поразмыслив немного можно доказать что IC = IA....
Подсказка 3
Посмотрим внимательно на утверждение из предыдущей подсказки. Да ведь из него напрямую выводится, что I лежит на серединном перпендикуляре к PQ ≥ I совпадает с R. Осталось просто посчитать углы на картинке.
Отметим на биссектрисе угла точку
— точку пересечения биссектрис треугольника
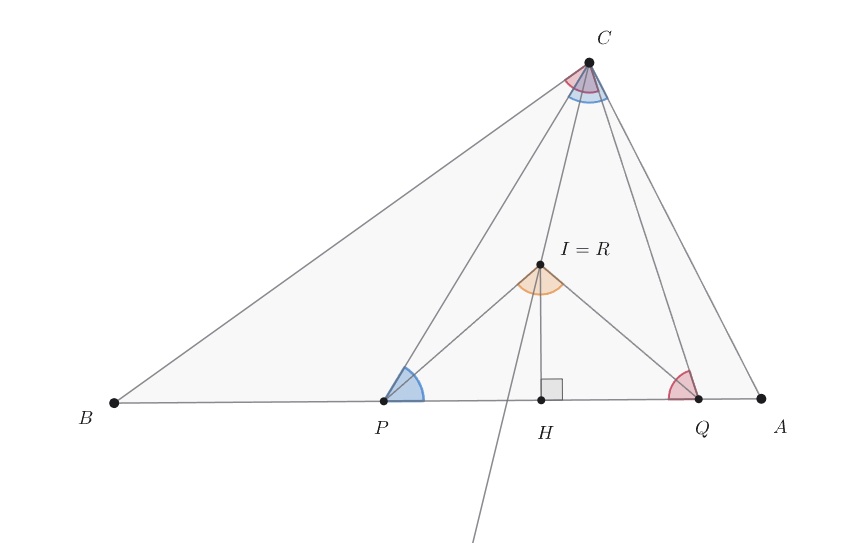
Тогда и
поэтому треугольники
и
равны по двум сторонам и углу между ними. Следовательно,
и
Аналогично доказывается, что
Стало быть,
и точка
лежит на серединном
перпендикуляре к отрезку
Но тогда она совпадает с точкой
поскольку является точкой пересечения тех же прямых.
Следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




