ПитерГор 2014 и ранее

Пример.

Два возможных примера показаны на рисунке.

Оценка.
Решение 1.
Рассмотрим произвольного ребёнка. Если он не видит уха, то он смотрит в чей-то затылок. Тогда стоящий перед ним либо видит чьё-то ухо, либо также смотрит в затылок. Таким образом, мы получаем цепочку из стоящих в ряд детей, в которой самый первый ребёнок видит чьё-то ухо. Заметим, что в этой цепочке не более ребёнка. Поскольку общее количество детей равно то цепочек не меньше чем Значит, их хотя бы Стало быть, как минимум ребёнка видят чьё-то ухо.
Решение 2.
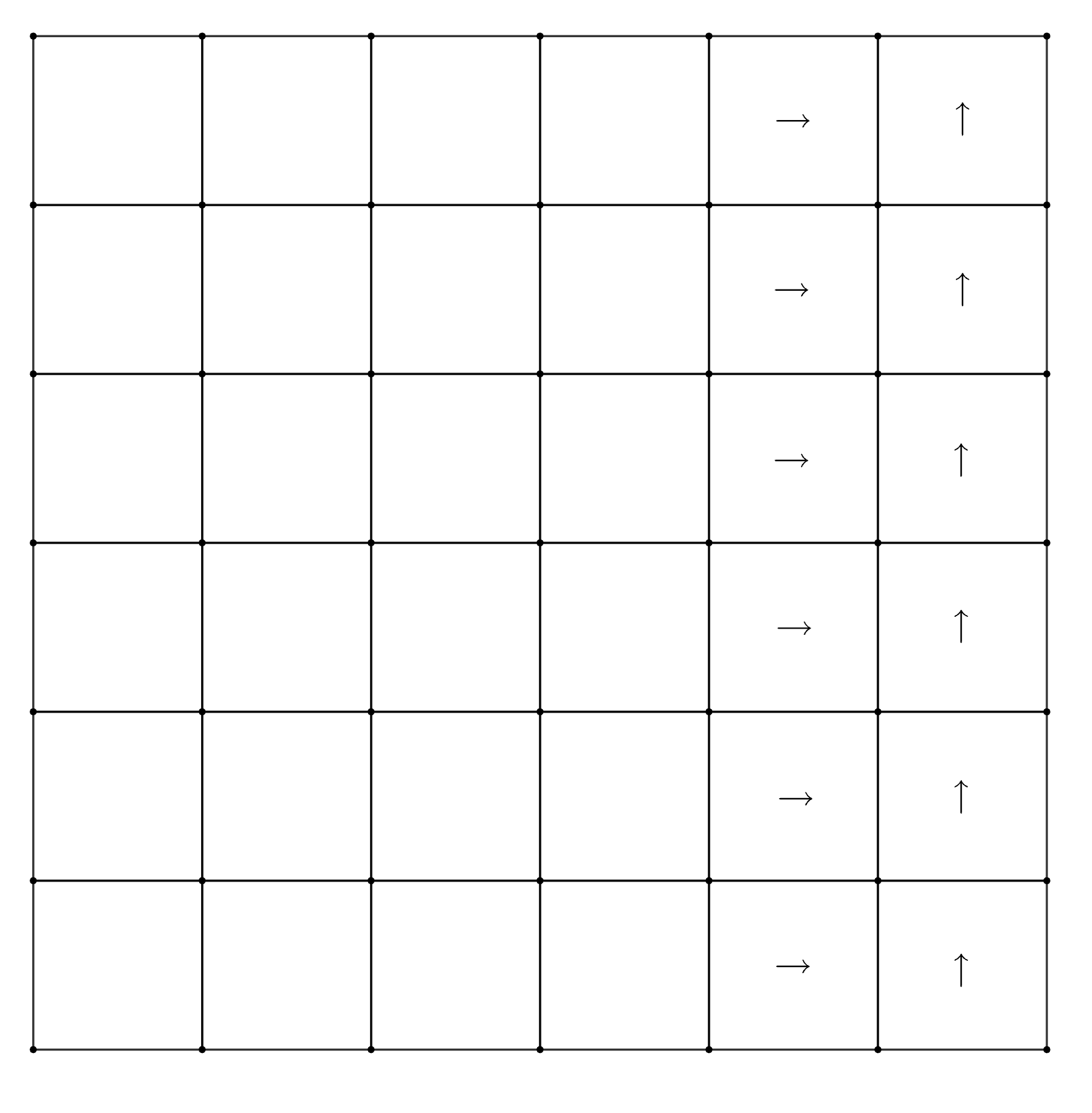
Рассмотрим произвольного ребёнка. Пусть для определённости он смотрит "вправо"(см. рис). Если он не видит уха, то он смотрит в чей-то затылок. Тогда стоящий перед ним также смотрит вправо и т.д., но самый правый ребёнок в этой строке должен смотреть вверх или вниз. Поэтому в этой строке есть хотя бы один ребёнок, который видит чьё-то ухо. Таким образом, если в какой-то строке есть ребёнок, смотрящий “горизонтально”, то в этой строке есть ребёнок, который видит ухо.

Если в каждой строке есть смотрящий горизонтально ребёнок, то в ней найдётся смотрящий горизонтально ребёнок, который видит ухо. Но все дети, чьи уши кто-нибудь видит, не могут стоять в одном столбце, поскольку в этом случае все они смотрят вертикально, что невозможно. Поэтому они стоят хотя бы в двух столбцах. Значит, в каждом из этих столбцов тоже хотя бы один ребёнок видит ухо. Таким образом, есть смотрящих горизонтально детей, которые видят ухо, и ещё не менее двух смотрящих вертикально детей, которые также видят ухо. Стало быть, детей, видящих ухо не менее чем

Рассмотрим теперь случай, когда в какой-то строке нет детей, смотрящих "горизонтально". Следовательно, они все смотрят "вертикально"и поворотом доски на этот случай сводится к уже рассмотренному.