ПитерГор 2014 и ранее
Ошибка.
Попробуйте повторить позже
Диагональ выпуклого четырёхугольника
делится точкой пересечения диагоналей пополам. Известно, что
На диагонали
нашлась точка
для которой
Докажите, что
Подсказка 1
В задачах, где один угол в два раза больше другого, бывает полезно найти равнобедренный треугольник, у которого угол при основании равен меньшему из указанных углов, тогда внешний угол при вершине, противоположной основанию, будет в два раза больше и, следовательно, равен большему из указанных.
Подсказка 2
На продолжении отрезка KD за точку D отложим отрезок DE, равный AD. Что можно сказать про прямые AE и BC?
Подсказка 3
Они параллельны. Как можно воспользоваться тем, что AC делится точкой пересечения диагоналей пополам?
Подсказка 4
Из этого и параллельности прямых AE и CB сразу следует, что ABCE — параллелограмм. Что при этом можно сказать про треугольник CEK?
Подсказка 5
Из указанного в условии соотношения на отрезки получим EK = КС, следовательно, EKC — равнобедренный. Как из этого следует требуемое соотношение на углы?
Пусть — точка пересечения диагоналей четырехугольника
тогда
На продолжении отрезка за точку
отложим отрезок
равный
Тогда
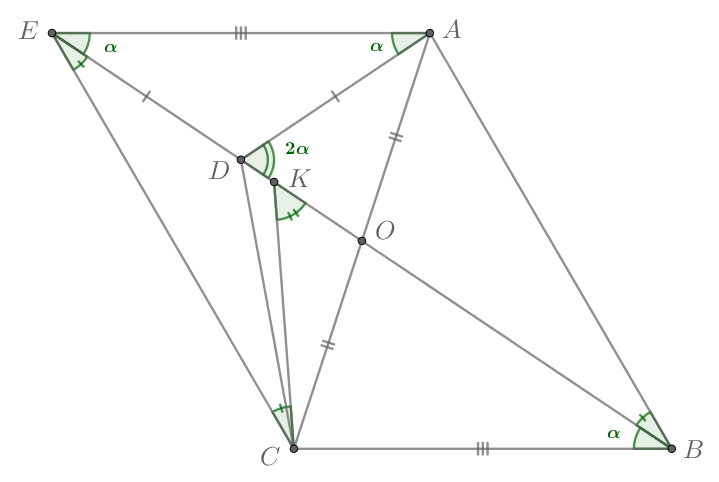
Пусть Тогда по условию
Так как
— внешний угол равнобедренного треугольника
то
Следовательно,
Тогда
Таким образом, треугольники
и
равны по
второму признаку. В равных треугольниках соответственные элементы равны, в частности,
Тогда
— параллелограмм.
Значит,
как накрест лежащие.
Так как — внешний угол равнобедренного треугольника
то
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




