Тема ПВГ - задания по годам

ПВГ 2019

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела пвг - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31286

Все 11-классники спецшколы разделены на три отдельные категории: экономисты, историки и филологи. На каждых двоих филологов приходится 3 человека, считающихся экономистами или историками, а на каждых пятерых экономистов приходится 7 человек, считающихся историками или филологами. Найдите количество историков, если 11-классников в школе не более 100.

Источники: ПВГ-2019, 11.1 (см. rsr-olymp.ru)

Подсказки к задаче

Подсказка 1

Введем переменные для количеств экономистов (x), историков (y) и филологов (z), и составим уравнения.

Подсказка 2

Уравнения составлены, но у нас три неизвестные и два уравнения - однозначно найти все не получится. Хочется выразить все переменные через одну, например, через z.

Подсказка 3

Все переменные - целые. Значит, мы можем воспользоваться делимостью! Действительно, если 11z = 24y и 25z = 24x, то z должно делиться на 24. Вспомним условие: школьников всего <= 100. Какие ограничения оно накладывает?

Подсказка 4

Из условия следует, что x + y + z <= 100. Осталось доказать, что при слишком больших z (z >= 48) это условие не будет выполняться.

Показать ответ и решение

Пусть экономистов, историков и филологов соответственно $x$ , $y$ и $z$ , тогда:

{ -z-= 2 { 3z = 2x+ 2y { 11z = 24y x+xy 35 =⇒ =⇒ z+y = 7 5z = 7x− 5y 25z = 24x

Все числа натуральные, потому $z$ кратно 24. Если $z ≥48$ , то $y ≥ 22,x ≥50$ , откуда сумма больше 100, а иначе $z = 24,y =11,x= 25$ .

Ответ:

$11$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#32156

Решите уравнение

2 x +8{x+ 4}− 9 =0

Источники: ПВГ-2019, 11.5 (см. rsr-olymp.ru)

Подсказки к задаче

Подсказка 1

Важный метод решения уравнений с целой и дробной частями: оценки сверху и снизу. Можно избавиться от большого количества иксов на оси справа, от большого количества иксов на оси слева и свести задачу к рассмотрению случаев: на каждом маленьком промежутке мы точно поймём, как раскроется дробная часть

Подсказка 2

Подумайте, так ли важна нам четвёрка внутри дробной части. Если мы к какому-то числу прибавим целое число, то изменится ли от этого дробная часть? Используйте оценку дробной части и это знание, чтобы оценить x^2-9, а потом и сам икс, сверху и снизу!

Подсказка 3

Осталось правильно разбить полученный промежуток на промежутки поменьше, чтобы дробная часть на них раскрылась однозначно. В каждом таком случае мы либо подставляем конкретный икс, либо получаем квадратное уравнение на икс с ограничениями на его значения (не забывайте эти ограничения при поиске корней учитывать!)

Показать ответ и решение

Так как ${x+ 4} ={x}= x− [x],$ то получаем

2 2 9 − x = 8x− 8[x] ⇐ ⇒ x + 8(x− [x])− 9= 0

Так как $0≤ {x+ 4}<1,$ то

2 0≤ 9− x = 8{x +4}< 8

1< x2 ≤9

Нужно рассмотреть случаи исходя из этой оценки

$∙$ Если $x= 3$ , то уравнение $x2+8(x− 3)− 9= 0$ обращается в тождество.

$∙$ Если $2≤x < 3$ , то $x2+8(x− 2)− 9= 0$ . Корни этого уравнения $− 4± √41$ и корень $− 4+ √41$ попадает в нужный полуинтервал.

$∙$ Если $1< x< 2$ , то $x2+8(x− 1)− 9= 0$ . Корни этого уравнения $− 4± √33$ и корень $− 4 +√33$ попадает в нужный полуинтервал.

$∙$ Если $− 2≤x < −1$ , то $x2+ 8(x+ 2)− 9 =0$ . Корни этого уравнения $− 7,−1$ и ни один не попадает в полуинтервал.

$∙$ Если $− 3≤x < −2$ , то $x2+ 8(x+ 3)− 9 =0$ . Корни этого уравнения $− 5,−3$ и корень $− 3$ подойдёт.

Ответ:

${−3;−4+ √33;−4+ √41;3}$

Ошибка.
Попробуйте повторить позже

Задача 3#37114

Две смежные боковые грани пирамиды, в основании которой лежит квадрат, перпендикулярны плоскости основания. Двугранный угол между двумя другими боковыми гранями равен $2π 3$ . Найдите отношение высоты пирамиды к стороне основания.

Источники: ПВГ-2019, 11.3 (см. rsr-olymp.ru)

Подсказки к задаче

Подсказка 1

В задаче уже есть прямые углы, поэтому давайте опустим из A и C высоты на BS, чтобы прямых углов появилось еще больше!;) Что можно сказать про эти высоты?

Подсказка 2

Проведенные высоты попадают в одну точку H на SB! Тогда можно построить плоскость AHC ;) ЧТо интересного можно сказать об этой плоскости?

Подсказка 3

BS перпендикулярная плоскости AHC! Значит, мы можем найти еще прямые углы, образованные прямой BS!

Подсказка 4

Пусть O — середина AC. Тогда угол OHS прямой! Как это можно связать с треугольником DSB?

Подсказка 5

Отлично, треугольники DSB и HOB подобны! Осталось всё аккуратно посчитать ;)

Показать ответ и решение

$PIC$

Пусть это пирамида $ABCDS$ , где $SD ⊥ ABCD$ (то есть основанию перпендикулярны $ASD$ и $CSD$ ). Обозначим сторону квадрата из основания за $a$ .

В силу симметрии высоты $AH$ и $CH$ к $BS$ пересекаются в одной точке. Тогда из условия $∠AHC =120∘$ , как угол между высотами к общей прямой двух плоскостей. Далее в силу той же симметрии $AH =HC$ и $AO = OC$ , то есть $AC ⊥ OH$ и $∠HCA = ∠HAC = 30∘$ . Отсюда $OH = OC tg30∘ = √a2 ⋅ 1√3 = √a6$ . Далее заметим, что $SB ⊥ ACH$ , поскольку перпендикулярна двум прямым $AH$ и $CH$ , откуда $OH ⊥ BS$ . Тогда $△BHO ∼ △BDS$ . Тогда $ODHS-= BBHD-$ . Осталось найти

∘---------------- ∘ --2-----2 2 (-a- --1--)2 ∘ -2--2-2 -a- BH = BC − CH = a − √2-⋅cos30∘ = a − 3a = √3 =⇒

a √- DS = OH-⋅BD- = √6 ⋅-2a-=a BH a√3

То есть высота пирамиды равна стороне основания.

Ответ:

$1 :1$

Ошибка.
Попробуйте повторить позже

Задача 4#39761

Сумма шести первых членов геометрической прогрессии, состоящей из положительных чисел, в $344$ раза больше суммы трех ее первых членов. Найдите знаменатель прогрессии.

Источники: ПВГ-2019, 11.1 (см. rsr-olymp.ru)

Подсказки к задаче

Подсказка 1

Обозначим первый член прогрессии b, а знаменатель q. Тогда что хорошего можно увидеть, когда мы запишем равенство на суммы из условия?

Подсказка 2

Верно, и слева, и справа есть b, на которое можно сократить и получить уравнение относительно одной переменной. Теперь применим формулу для суммы геометрической прогрессии. У нас получается там 6 степень... Как можно упростить себе жизнь, вспомнив, что это q^3 в квадрате?

Подсказка 3

Ага, мы можем разложить скобку слева по формуле разности квадратов! Теперь мы можем сократить общую часть и легко найти q.

Показать ответ и решение

Пусть $b = b,b = bq. 1 2$ Тогда условие можно переписать в виде

5 2 1−-q6 1− q3 b+ bq +...bq = 344(b+ bq+ bq) ⇐⇒ 1− q = 3441− q ⇐ ⇒

⇐⇒ (1− q3)(1+ q3)= 344(1− q3) ⇐ ⇒ q = 7

Здесь мы считаем $q ⁄=1,$ однако легко видеть, что при $q = 1$ условие не выполнено.

Ответ:

$7$

Ошибка.
Попробуйте повторить позже

Задача 5#40086

Аня выписала одно за другим $2018$ чисел

1⋅2 2⋅3 3⋅4 2018-⋅2019 2 , 2 , 2 ,..., 2

и вычислила их. Сколько из получившихся чисел имеют в десятичной записи последнюю цифру 5?

Источники: ПВГ-2019, 11.2 (см. rsr-olymp.ru)

Подсказки к задаче

Подсказка 1!

Итак, в задаче надо выяснить, как часто последняя цифра будет 5. Давайте просто возьмем и попробуем написать последние цифры у некоторого количества чисел из последовательности.

Подсказка 2!

Так как нам нужно посчитать, как часто встречается 5, было бы здорово заметить какую-то периодичность... Можно, конечно, просто повыписывать числа, но давайте попробуем проанализировать. Нам даны числа вида N(N+1)/2 и мы хотим чтобы у этого совпала последняя цифра с каким-то (N+X)(N+1+X)/2, это будет значить, что у нас период длины Х!. Что же это может быть за Х...

Подсказка 3!

Ага, нехитрыми алгебраическими вычислениями заметим, что 20 подойдет! Ну все, самое важное мы уже сделали, осталось как-то хитро (или не очень) подсчитать 5ки!

Показать ответ и решение

Поскольку для любого натурального $n$ от $1$ до $(2018− 20)$ разность $(n+20)⋅(n+21)-− n⋅(n+1)= 20n +210 2 2$ делится на $10,$ то числа $(n+20)⋅(n+21) 2$ и $n⋅(n+1) 2$ заканчиваются на одну и ту же цифру, то есть последовательность последних цифр данных в условии чисел периодическая с периодом $T = 20.$

Также заметим, что $n⋅(n+1) 2 = 1+ ...+n.$ Можно легко выписать последние цифры первых $20$ чисел, прибавляя к предыдущему номер текущего числа и беря остаток по модулю $10:1,3,6,0,5,1,8,6,5,5,6,8,1,5,0,6,3,1,0,0.$

В группе из $20$ чисел цифра $5$ встречается $4$ раза. Среди $2018$ чисел есть $100$ групп по $20$ чисел и последняя группа на $18$ чисел, а которой также четыре пятёрки. В итоге всего пятёрок $100⋅4 +4 =404$ штуки.

Ответ:

$404$

Ошибка.
Попробуйте повторить позже

Задача 6#45074

В равнобедренном треугольнике $ABC$ на высоте $BH$ , равной основанию $AC$ , как на диаметре построена окружность, пересекающая боковую сторону $BC$ в точке $F$ . Каково отношение площади треугольника $FCH$ к площади треугольника $ABC?$ Какая часть площади треугольника $ABC$ находится внутри окружности?

Источники: ПВГ-2019, 11.4 (см. rsr-olymp.ru)

Подсказки к задаче

Подсказка 1!

Давайте обозначит CF за x и попробуем посмотреть, что у нас получается. Основание треугольника обозначим за 2a. Давайте обозначим еще оснаток BF за y. Мы знаем, что трегуольник BFH прямоугольный, тогда давайте воспользуемся теоремой о соотношении катетов в прямоугольном треугольнике! Попробуйте найти отношение y/x.

Подсказка 2!

Да, записав теорему мы получим, что это соотношение равно 4. Осталось только найти соотношение площадей)

Подсказка 3!

Так, займемся пунктом b. Было бы здорово попробовать избавиться от x и выразить его через a. Для нахождения площади сегментов окружности, нам придется обратиться к цглам и центру. Отметьте центр окружности и заметим, что тогда в треугольнике BOF можно написать теорему косинусов! Остается аккуратно посчитать и ответить на вопрос.

Показать ответ и решение

$PIC$

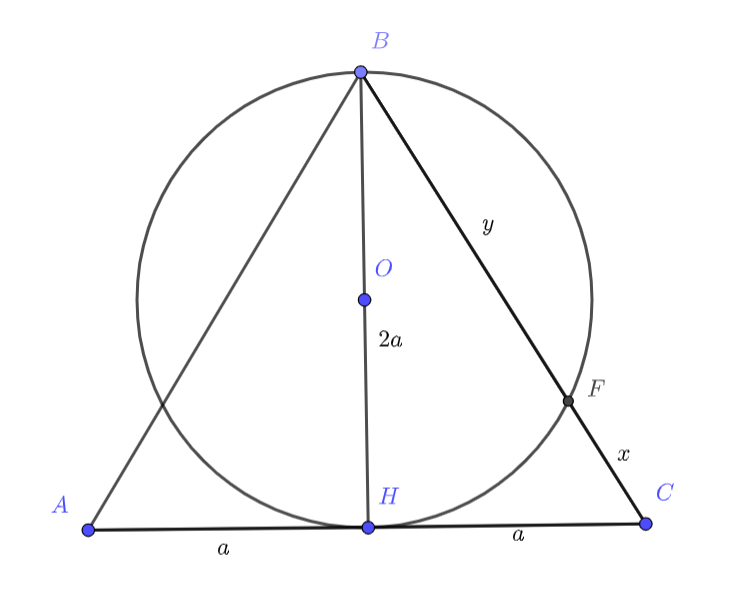
Введем обозначения: $BH = 2a,HC =a,BF = y,F C = x$ . Поскольку угол $BF H$ - прямой, то по теореме об соотношениях в прямоугольном треугольнике для двух катетов $BH,HC$ будем иметь:

{ a2 = x(y+ x), ⇒ y= 4⇒ y = 4x 4a2 =y(x+ y) x

Из отношения площадей треугольников с общим углом находим ответ на первый вопрос:

SFSCH- = 2a(axx+-y) = 110 ABC

Из теоремы Пифагора для $△BHC$ имеем $5a2 = 25x2 =⇒ x= √a 5$ . Далее пусть $O$ — центр окружности из условия, а также $∠HOF =α$ , запишем теорему косинусов для $△BOF$

(-4a-)2 2 2 3 4 √5- = 2a +2a cosα ⇒ cosα = 5 ⇒ sin α= 5

Обозначим площадь сектора $HOF$ через $S1$ . Тогда $1 2 4 S1 = 2a ⋅arcsin 5$ . Внутри окружности у треугольника два таких сектора. Кроме того, внутри окружности два треугольника одинаковой площади (симметрия относительно $BH$ ). Найдем площадь $S2$ $1 2 △BOF :S2 = 2a2sinδ = 5a2$ . Тогда ответ на второй вопрос будет следующий: $2(S +S) 1( 4 4) -S1ABC2-= 2 arcsin5 +5$ .

Ответ:

$-1, 1(arcsin4 + 4) 10 2 5 5$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#47066

Определите значение функции:

5 4 3 2 f(x)=x + ax + bx + cx +dx+ e

в точке $x= 2018$ , если

f(2019)= f(2023)= 0, f(2020)=f(2022)= −3, f(2021)= −4.

Источники: ПВГ-2019, 11.5 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1!

Давайте попробуем сделать условие более симметричным - например, завести новую функцию g(x) = f(x + 2021)

Подсказка 2!

Наша цель - узнать что-то полезное про это равенство пятой степени. Для этого давайте попробуем сделать такую функцию, чтобы все наши значения были ее корнями.

Подсказка 3!

Например, подойдет m(x) = g(x) - x^2 + 4. Заметим, что теперь все наши числа из условия дают 0 этой функции. Осталось проанализировать получившееся!

Показать ответ и решение

Рассмотрим $g(x)= f(x +2021)$ . Тогда

5 4 3 2 g(x)= x +px + qx +vx + ux+ w,

при этом

g(−2)=g(2)= 0,g(−1)=g(1)=− 3,g(0) =− 4.

Рассмотрим $h(x) =g(x)− x2+ 4.$ Тогда

h(−2)= h(2) =0− 4+ 4= 0,h(−1)= h(1)= −3− 1+ 4= 0,h(0)=g(0)− 0+ 4= 0.

При этом $h(x)$ также остаётся многочленом пятой степени. Поэтому он имеет не больше пяти корней, при этом пять корней мы уже нашли, так что по теореме Безу $h(x)= x(x − 1)(x +1)(x − 2)(x +2).$

Искомое значение

f(2018)= f(− 3+2021)= g(−3)= h(− 3)+ (−3)2 − 4=

= −3⋅8⋅5+ 9− 4= −120+5 =− 115.

Ответ:

$− 115$

Ошибка.
Попробуйте повторить позже

Задача 8#63894

В основании пирамиды $SABC$ лежит треугольник $ABC$ со сторонами $AB = BC = 3√2-$ и $AC =2√6$ . Высота пирамиды равна $√ - 6$ и видна из вершин $A$ и $C$ под одним и тем же углом, равным $√1 arcsin 3$ . Под каким углом она видна из вершины $B?$

Источники: ПВГ-2019, 11.4 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Пусть SH – высота пирамиды, подумайте, на каком значимом отрезке в треугольнике лежит точка Н?

Подсказка 2

Она лежит на медиане, биссектрисе и высоте треугольника △АВС! Тогда мы без труда сможем выразить ВН через стороны треугольника и данные/интересующие нас уголочки (только не забудьте рассмотреть два случая: ведь точка Н может лежать как внутри, так и вне треугольника △АВС), откуда мы и можем найти тригонометрическую функцию искомого угла

Показать ответ и решение

Поскольку высота $SH$ пирамиды видна из вершин $A$ и $C$ под одним и тем же углом, точка $H$ лежит на медиане (она же биссектриса и высота) $BM$ треугольника $ABC$ или её продолжении.

$PIC$

Если $SH =h,AB = BC =a$ , $AC = b$ и $∠SAH = ∠SCH = α$ , а искомый угол $∠SBH = β$ , то имеем

∘------ ∘ ----------- BH = hctgβ =BM ±MH = a2− b2± h2 ctg2α− b2, 4 4

откуда, подставляя данные задачи, получаем $√- ctgβ = 2± 1$ , в зависимости от того, лежит ли точка $H$ внутри треугольника $ABC$ или вне него. Значит, $π β = 8$ или $3π β = 8 .$

Ответ:

$π∕8$ или $3π∕8$

Ошибка.
Попробуйте повторить позже

Задача 9#65353

Найдите все возможные значения величины

-----f(t)−-f(0)----- T = f (t2)+f(t)− 2f(0)+ 2,

если $f(2x+ y)− f(x+ y)= 2x$ для всех действительных значений $x$ и $y.$

Источники: ПВГ-2019, 11.3 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Вначале забудем про T и попробуем решить фуру. Тут есть очень удобная подстановка, которая позволяет избавиться от одной из переменных. Какая?

Подсказка 2

Можно подставить y=-x, и тогда сразу находим функцию f(x)=2x+C.

Подсказка 3

Теперь подставляем в T и получаем выражение, значения которого можно исследовать с помощью производной.

Показать ответ и решение

Если подставить в функциональное равенство $y =− x$ , мы получим, что $f(x)− f(0)= 2x$ . Следовательно, числитель $T$ равен $2t.$

Если подставить $2 2 x= t,y = −t$ , мы получим, что $2 2 f(t )− f(0)=2t$ . Следовательно, знаменатель $T$ равен $2 2t+ 2t+2.$

Таким образом, $--t-- T = t2+t+1.$

С помощью производной или неравенства о средних можно выяснить, что:

при $1 --1-- 1 t> 0 1+ t+ t ≥ 3 =⇒ 0< T = 1+t+1t ≤ 3;$

при $t= 0 T =0;$

при $1 1 t< 0 1+ t+ t ≤ −1 =⇒ − 1≤ T = 1+t+-1t < 0.$

Ответ:

$[−1;1] 3$

Ошибка.
Попробуйте повторить позже

Задача 10#67143

Найдите все тройки натуральных чисел $(m,n,k)$ такие, что

3 3 m +n = k!+32

Источники: ПВГ-2019, 11.4 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Когда в задаче на натуральные числа внезапно начинают фигурировать кубы, то пусть у вас всегда возникает мысль, что надо работать по модулю 7 или 9. Это потому, что там очень мало остатков получается. Поработаем, к примеру, с 7. Что мы можем сказать про правую часть при k > 6?

Подсказка 2

Верно, справа по модулю 7 будет 4, так как k! делится на 7, а остаток 32 по модулю 7 это 4. А слева какие вообще выражения могут быть по модулю 7? Какие вообще значения может принимать куб числа по модулю 7?

Подсказка 3

Верно, левая часть по модулю 7 никогда не сравняется с правой, а значит, мы ограничили k сверху шестёркой. Остается перебрать все возможные k и попытаться найти для них подходящие натуральные m и n. Задача решена!

Показать ответ и решение

Посмотрим по модулю $7.$ Нетрудно проверить, что кубы натуральных могут давать только остатки $0,1,−1$ (можно для удобства заменить остаток $6$ на $− 1,$ очевидно, что разница кратна $7$ ). Поэтому если $k≥ 7,$ то правая часть даёт остаток $4$ по модулю $7$ (такой же, как $32$ ). При этом остатки левой части могут быть только ${−2,−1,0,1,2}.$ Все они отличаются от $4$ по модулю $7,$ поэтому равенство невозможно. Значит, $k ≤6.$ Остаётся перебрать случаи

$3 3 k =1.m + n = 33,$ решений нет.
$3 3 k =2.m + n = 34,$ решений нет.
$3 3 k =3.m + n = 38,$ решений нет.
$k =4.m3+ n3 = 56,$ решений нет.
$k =5.m3+ n3 = 152,$ решения $(3,5),(5,3).$
$k =6.m3+ n3 = 752,$ решений нет.

Все проверки осуществляются простым перебором (достаточно взять $n,m ≤9,$ поскольку $93 = 729$ для последнего случая, а для других намного меньше).

Замечание. Аналогичные рассуждения можно было провести для модуля $9,$ тогда не потребовалось бы рассматривать $k =6.$

Ответ:

$(5,3,5),(3,5,5)$

Ошибка.
Попробуйте повторить позже

Задача 11#67534

Все 11-классники спецшколы разделены на три отдельные категории: физики, химики и биологи. На каждых двоих биологов приходится 5 человек, считающихся физиками или химиками, а на каждых троих физиков приходится 7 человек, считающихся химиками или биологами. Найдите количество химиков, если 11-классников в школе не более 100.

Источники: ПВГ-2019, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Пусть x, y, z — количество учеников в категории: биологии, химики, физики. Перепишите условие задачи в данных терминах.

Подсказка 2

Можно подобрать значения и убедиться, что одиннадцатиклассников в школе не более 100.

Показать ответ и решение

Пусть $x,y,z$ — количество учеников в категории: биологии, химики, физики. Тогда по условию задачи получим систему уравнений:

({ 5x= 2(y+z) ( 7z = 3(x+y)

( { 5x − 2y = 2z ( 7z =3x+ 3y

( { 5x− 14z3-+2x= 2z|⋅3 ( 7z y = 3 − x|⋅21

({ 21x= 20z ( 21y = 49z− 20z = 29z

({ 21x= 20z ( 21y = 29z.

Это значит, что минимальные значения могут быть только: $x= 20,y = 29,z =21.$

Ответ:

$29$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#80265

Решите неравенство

∘--------√----- ∘ --------√----- ( 17) 4x+ 1− 12 x− 2+ 4x+ 8− 16 x− 2 ≤log1∕4 x− 4

Источники: ПВГ 2019

Подсказки к задаче

Подсказка 1

Корень под корнем - не самая приятная вещь, давайте проведём замену t=√(x-2). Тогда x=t²+2. При подстановке в выражении выделяются полные квадраты, корни исчезают, и остаётся просто неравенство с логарифмом и модулями. Что мы можем сказать о возможных значениях t?

Подсказка 2

Конечно, из ОДЗ на x следует, что t больше 3/2. Давайте теперь посмотрим, как раскрываются модули при разных значениях t.

Подсказка 3

Верно, при t≤2 все t сокращаются. Тогда остаётся рассмотреть отдельно эти два случая (когда t сокращается и когда нет) и аккуратно найти объединение решений в каждом из случаев

Показать ответ и решение

Сделаем замену $t=√x-−-2, t≥0.$ Тогда сведем неравенство к следующему виду, предварительно собрав полные квадраты

( 17) |2t− 3|+ |2t− 4|≤ log14 x− 4

Так как $x> 174 ,$ то $t> 32.$

При $( ] t∈ 32;2$ получаем

( ) 1≤ log14 x− 17 , 4

откуда $x ∈(147;92]$

При $t> 2$ получаем

( ) 4t− 7 ≤log1 x− 17 4 4

Так как $t> 2,$ то левая часть уравнения больше $1.$ С другой стороны при $t> 2$ получаем , что $x> 6,$ а тогда $( 17) x− 4 >1$ и $( 17) log14 x− 4 <0.$

Ответ:

$(17;9] 4 2$

Ошибка.
Попробуйте повторить позже

Задача 13#80267

Для каждого значения параметра $a$ решите уравнение

|| sin21(2a)|| || −4tg(3a)|| ( -π)2( -π) ||x− 2 ||+ |x− 2 |+a a +12 a− 12 =0.

Подсказки к задаче

Подсказка 1

По-видимому, нормальным решением уравнения здесь и не пахнет... Когда кажется, что все печально, в голову приходит супер-мысль: вспомнить про метод оценки! У нас слева стоит сумма двух модулей и какое-то выражение. Тогда рассчитывать на решения стоит тогда, когда это выражение неположительное...

Подсказка 2

Оно неположительно, когда 0≤a≤π/12 или a=-π/12. У нас имеется сумма двух модулей, поэтому очень хочется воспользоваться неравенством |x|+|y|≥|x-y|...

Подсказка 3

В силу монотонности синуса 1/sin²2a≥1/sin²(π/6)=4 при a∈(0;π/12], а также -4tg3a<0. Поэтому модуль разности наших модулей будет больше 15. Покажите, что при a∈(0;π/12] выражение a(a+π/12)²(a-π/12) не будет превосходить 1 и доведите решение до конца!

Показать ответ и решение

Решение может существовать только если

{ π-} ( π-] a ∈ − 12 ∪ 0; 12

поскольку иначе левая часть уравнения или не определена, или строго положительна.

При $π a= − 12-$ уравнение имеет вид

2|x− 16|=0

Следовательно, при $-π a= −12$ получаем решение $x= 16.$

Если $( π-] a∈ 0;12 ,$ то

--1-- 2 sin2(2a) > 16, 2−4tg(3a) < 1

Поэтому минимум функции

||| sin12(2a)||| || −4tg(3a)|| f(x)= |x − 2 |+ |x − 2 |

не меньше $15.$ С другой стороны абсолютное значение выражения

( ) ( ) g(a)= a a+ -π 2 a− π- 12 12

на полуинтервале $(0; π12)$ заведомо не больше $1 :$

|g(a)|< a(a+ π-)3 < 1 12

Поэтому при $a∈(0; π-] 12$ решений нет.

Ответ:

$x =16$ при $a= −-π; 12$

при остальных значениях $a$ решений нет.

Ошибка.
Попробуйте повторить позже

Задача 14#80581

Решите неравенство

arcsin(sin|x|)≥arccos|cos3x|

Источники: ПВГ 2019

Подсказки к задаче

Подсказка 1

Попробуйте заметить симметрию.

Подсказка 2

Если x нам подойдет, тогда -x — тоже. Будем теперь считать, что x ≥ 0. Какой еще значение может подойти, если x подходит?

Подсказка 3

Если x — подходит, тогда и x + 2π подходит. Будем считать, что x меньше 2π.

Подсказка 4

Оцените величины аркфункций на интервале [0; 2π).

Подсказка 5

Заметим, что интервал (π; 2π) нам не подходит.

Показать ответ и решение

Заметим, что если $x$ подходит, то и $− x$ подходит. Тогда давайте считать, что $x≥ 0$ .

Так же если $x$ , $x +2π$ больше 0 и $x$ подходит, то и $x+ 2π$ подходит. Значит, можно считать, что $x∈ [0,2π)$ .

Теперь заметим, что $x ∈(π,2π)$ не подходит, так как тогда $arcsin(sin|x|)<0 ≤arccos|cos3x|$ .

Нарисуем график для $x∈[0,π]$ . На этом интервале нам подходят $[π 3π] x∈ 4,4$ . Значит, на интервале $[0;2π]$ нам подходит только $[π 3π] x ∈ 4, 4$ . Осталось распространить это на всю прямую. Значит,

[π 3π ] [ −3π π ] x∈ ∪k≥0 4 + 2πk,4 +2πk ∪k≥0 -4-− 2πk,− 4p− 2πk

Ответ:

$[π + 2πk,3π+ 2πk]∪[−3π− 2πk,− πp− 2πk],k∈ {0} ∪ℕ 4 4 4 4$

Ошибка.
Попробуйте повторить позже

Задача 15#86091

Решите уравнение в целых числах:

2 3xy− x− y = 2019− 3x

Источники: ПВГ 2019

Подсказки к задаче

Подсказка 1

Как было бы удобнее работать с данным уравнением?

Подсказка 2

Перенесите все неизвестные в левую часть и разложите на множители.

Подсказка 3

Посмотрите на остатки.

Показать ответ и решение

Перенесём все неизвестные в одну сторону и разложим на множители:

2 3x + 3xy− x − y =2019

3x(x +y)− (x +y)= 2019

(3x− 1)(x+ y)=2019

Заметим, что $2019 =3⋅673,$ где каждый сомножитель простой, и что выражение в первой скобке даёт остаток 2 по модулю 3, значит, оно должно быть равно числу с остатком 2 по модулю 3. Посмотрим остатки всех целых делителей числа 2019 по модулю 3: у 2019 остаток 0, у 673 остаток 1, у 3 остаток 0, у 1 остаток 1, у $− 1$ остаток 2, у $− 3$ остаток 0, у $− 673$ остаток 2, у $− 2019$ остаток 0.

Следовательно, возможно только два случая

{ { 3x − 1 =− 1 3x− 1= −673 x+y =− 2019 и x+ y = −3

{ { x= 0 и x = −224 y = −2019 y =221

Ответ:

$(0;− 2019),(−224;221)$

Ошибка.
Попробуйте повторить позже

Задача 16#92323

Найдите десятичную запись числа

5 ( 2) - (∘ 3√----) 10-⋅-2x− x-+ 2(3√2+ 1)(3 --2− 1) 666 3

если $x =0,999.$

Источники: ПВГ 2019

Подсказки к задаче

Подсказка 1

Первое слагаемое придется честно вычислить. Для этого удобно сначала вычислить 2x - x² = x(2-x), заметив, что 0,999 = 1 - 0,001. А как можно вычислить второе слагаемое?

Подсказка 2

Ясно, что простыми тождественными преобразованиями тут не обойтись. В выражении второго слагаемого фигурирует много кубических корней. Как можно уменьшить их количество?

Подсказка 3

Верно! Вместо самого второго слагаемого сначала попробуем вычислить его куб! Что тогда получится?

Показать ответ и решение

Так как $x= 1− 10−3,$ то

2 ( −3)( −3) −6 2x− x = x(2 − x)= 1− 10 1+10 = 1− 10 =0,999999

Поэтому

(2x − x2)⋅105 99999,9 ----666-----= -666--= 150,15

Обозначим второе слагаемое $3√- (∘3√32−1) 2( 2 +1) --3- = y.$ Так как

( 3√- ) √3- √3- 3√- y3 = 8(3√2+ 1)3 -2-− 1 = 8⋅ (2+3-4+3--2+-1)(-2−-1) √- 3√- √- √- √-3 =8 ⋅ 232+-3⋅2+-334+-32−-2−-334−-332−-1-=8 3

то $y = 2$ (понятно, что $y >0,$ так как все множители положительные).

Ответ:

$152,15$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#113664

При каких значениях $a$ существует $b$ такое, что уравнение

2 2 sin bsinx+ cos bcosx =a

не имеет решений?

Источники: ПВГ 2019

Подсказки к задаче

Подсказка 1

Как можно преобразовать выражение в левой части?

Подсказка 2

Примените метод вспомогательного аргумента, введя f(b) = √(sin⁴b + cos⁴b).

Подсказка 3

Воспользуйтесь тем, что косинус по модулю не превосходит единицу.

Показать ответ и решение

Пользуясь методом вспомогательного аргумента, приходим к уравнению

a= f(b)cos(x− f(b)),

где

∘ --4-----4- f(b)= sin b+ cos b

Если $| a-|≤ 1 f(b)$ при любых $b,$ то найдётся, например, решение $x= f(b)+ arccos-a. f(b)$ А если же при каком-то $b$ выполнено $| a-|> 1, f(b)$ то у уравнения решений нет, так как косинус по модулю не больше единицы.