Тема ПВГ - задания по годам

ПВГ 2016

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела пвг - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31498

Найдите наименьшее натуральное число $N,$ такое что число $99N$ состоит из одних троек.

Подсказки к задаче

Подсказка 1

Сперва посмотрим, на что делится число 99N: на 9 и 11. Можем ли мы что-нибудь сказать про количество цифр?

Подсказка 2

В силу того, что число состоит только из троек, из признака делимости на 9 следует, что кол-во цифр делится на 3. А из признака делимости на 11 следует, что кол-во цифр должно делиться на 2. Тогда оно делится на 6. Какое тогда может быть минимальное подходящее число?

Подсказка 3

Нетрудно понять, что это 333333. Отсюда находится N.

Показать ответ и решение

Заметим, что число $99N$ делится на $9$ и на $11.$ Значит, количество цифр в нём должно делиться на $3$ и на $2$ (то есть и на $6$ ), так как если число троек нечётное, то сумма на чётных и нечётных местах будет отличаться на $3$ — не соответствует критерию делимости на 11. Отсюда $99N ≥333333$ и при этом $99N = 333333$ уже подходит, так что наименьшее $N = 3367.$

Ответ:

$3367$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#34203

Решите уравнение

10 10 29- 4 sin x+cos x = 16 cos 2x.

Источники: ПВг-2016, 11.3 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Вот наверняка у вас возникал вопрос: зачем учить формулы понижения степени? Ответ: для того, чтобы сейчас же понизить эти десятые степени! Помним, что sin¹⁰(x) = (sin²(x))⁵. Там начнет фигурировать и пятая степень двойки - на нее стоит домножить левую и правую части.

Подсказка 2

Заменим cos(2x) на t, а затем, не стесняясь, раскроем скобки с пятыми степенями. Вы же понимаете, что при раскрытии они будут почти идентичны? Только слагаемые с нечетной степенью будут отличаться знаками, следовательно, при сложении они просто пропадут!

Подсказка 3

Далее будет очень удобно сделать замену t² = p, тогда мы получим квадратное уравнение, решим его и сделаем обратную замену, таким образом постепенно и дорешаем задачу.

Показать ответ и решение

Первое решение.

По формуле понижения степени уравнение равносильно

5 5 4 (1 − cos(2x)) + (1 +cos(2x)) = 29⋅2⋅cos (2x).

После замены $cos(2x)= t$ и раскрытия скобок имеем (нечётные степени косинуса взаимноуничтожаются):

2 4 4 1+10t +5t = 29t .

Из этого квадратного относительно $t2$ уравнения получаем $t2 = 12$ или $t2 = −112$ . Отсюда $cos(2x)= ±√1 2$ , так что $x =± π8 + πk2 = π8 + π4k,k ∈ℤ$ .

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Выразим две суммы с меньшими степенями через $cos4x$

sin4x+ cos4x= 1− 2sin2xcos2x =1 − 1 sin22x= 3+-cos4x 2 4

6 6 4 2 2 4 3 2 3cos4x+-5- sin x +cosx =sinx − sin x cos x+ cos x= 1− 4sin 2x = 8

Теперь выразим через них левую часть

sin10x+ cos10x= (sin4x +cos4x)(sin6x+ cos6x)− sin4x cos4x

( )2 sin4xcos4x = 1-sin42x= 1- 1-− cos4x = 1-(1 − 2cos4x+cos24x) 16 16 2 64

Теперь подставим всё это в изначальное равенство

3+-cos4x ⋅ 3cos4x+-5− 1−-2cos4x-+cos2-4x = 29(cos24x +2cos4x+1) 4 8 64 64

2 2 2 6cos 4x+ 28cos4x+ 30− 1+2cos4x− cos 4x= 29 cos 4x+58cos4x+29

2 24cos4x+ 28cos4x =0 ⇐⇒ cos4x =0,−7∕6

Остаётся только первый корень, который и идёт в ответ.

Ответ:

$π + πn, n ∈ℤ 8 4$

Ошибка.
Попробуйте повторить позже

Задача 3#34644

На соревнования по лёгкой атлетике ученики школы приехали на автобусе, вмещающем не более 40 человек. Каждый из них участвовал в одном из видов соревнований. При этом $1∕7$ часть учеников завоевали золотые медали, $1∕4$ часть — серебряные и ещё $1∕4$ — бронзовые. На обратном пути медалисты решили собрать деньги и купить по одному торту каждому из спортсменов, оставшемуся без медалей. Сколько тортов им придётся покупать?

Источники: ПВГ-2016, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Сразу заметьте, что информация про автобус говорит нам о том, что человек может быть от 1 до 40... Просто рассмотрите 40 вариантов! Но, конечно же, задача не об этом. Подумайте, как информация про завоеванные медали поможет этот перебор сократить

Подсказка 2

Если нам говорят о том, что 1/n часть учеников что-то там получила, то, выходит, количество учеников мы смогли поделить на n, то есть это количество было кратно n. А условия на кратности уже сильно сокращают варианты для общего количества человек в автобусе!

Показать ответ и решение

Из условия следует, что число учеников должно быть кратно $4$ и $7.$ В силу взаимной простоты этих чисел количество учеников должно быть кратно $28.$ Но раз оно не больше $40,$ то учеников ровно $28.$ Отсюда медали завоевали $28- 28- 7 +2⋅ 4 =18.$ Соответственно без медалей остались $10$ человек, столько и надо купить тортов.

Ответ:

$10$

Ошибка.
Попробуйте повторить позже

Задача 4#36853

Футбольный мяч шьётся из $32$ кусочков кожи: белых шестиугольников и чёрных пятиугольников. Каждый чёрный кусочек граничит только с белыми кусочками, каждый белый кусочек граничит с тремя чёрными и тремя белыми. Сколько чёрных кусочков нужно для изготовления мяча?

Источники: ПВГ-2016, 11.2 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1!

Итак, у нас в задаче есть многоугольники, которые друг с другом граничат, было бы удобно выбрать какую-то величину и считать ее с помощью условий...

Подсказка 2!

Так-так-так, у нас есть некоторая величина, например, количество границ черных и белых многоугольничков, про которую мы знаем и от белых многоугольников, и от черных... Что бы тут могло значить?

Подсказка 3!

Именно! Количество связей белых клеток с черными у нас считается с двух разных сторон! Это должно помочь...

Показать ответ и решение

Из условия получаем, что $x$ чёрных кусочков граничат суммарно с $5x$ белыми, соответственно $32 − x$ белых кусочков граничат с $3(32 − x)$ чёрными. То есть число границ между белыми и чёрными кусочками равно с одной стороны $5x,$ а с другой стороны $96− 3x.$ Отсюда находим, что $96 x= 8 = 12.$

Ответ:

$12$

Ошибка.
Попробуйте повторить позже

Задача 5#38134

Решите уравнение

∘----√- (1− log2x)⋅ logx2 x = 1

Источники: ПВГ-2016, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Для начала, конечно же, запишем ОДЗ! Теперь анализируем уравнение: метод рационализации здесь нам вряд-ли поможет, есть 2 логарифма, и по итогу хотелось бы их преобразовать к одинаковому виду и сделать замену.

Подсказка 2

Как их преобразовывать? Например, из первой скобки можно сделать один логарифм, а во втором логарифме избавиться от √х и разложить полученный логарифм на 2 хороших слагаемых!

Подсказка 3

Итак, по итогу мы можем из обоих логарифмов получить log_(x/2) 2, или подобный логарифм. Осталось лишь сделать замену этого логарифма на новую переменную, решить уравнение относительно неё, вернуться к логарифмам и учесть ОДЗ!

Показать ответ и решение

ОДЗ:

(| x >0 { x ⁄= 1 |( 2 √- logx∕2 x ≥0

На ОДЗ по свойствам логарифмов получаем уравнение

( 2) ∘ 1-----x--- log2x ⋅ 2 logx2(2 ⋅2)= 1

( ) ∘ -------- √ - − log2 x ⋅ 1+ logx2 2= 2 2

− ∘1+-logx-2= √2⋅logx 2 2 2

При замене $t=logx2 2$ после возведения в квадрат (не равносильный переход, а следствие, так что корни проверим) получаем

1+ t=2t2 ⇐⇒ t∈{1;− 1} 2

Обратная замена:

t=1 −→ x =2 ⇐ ⇒ x =4 2

1 ∘-2 1 t= −2 −→ x = 2 ⇐⇒ x= 2

После подстановки в исходное уравнение получаем, что $x= 4$ не подходит, а $1 x= 2$ подходит.

Ответ:

$1 2$

Ошибка.
Попробуйте повторить позже

Задача 6#38686

Решите неравенство

(log √x+1)−1 2 log3x(x+ 1)− (x+ 1) cos5 < sin 5.

Источники: ПВГ-2016, 11.2 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

В условии дана какая-то странная степень, можно ли из неё получить что-то хорошее?

Подсказка 2

Давайте получим логарифм с основанием x+1

Показать ответ и решение

ОДЗ: $x> 0,3x ⁄=1$ . Поскольку $(log √x+-1)−1 =2log cos5 cos5 x+1$ , то имеем

2 2 log3x(x+ 1)− cos 5< sin 5 ⇐⇒ log3x(x+ 1)<1

Если $x< 1 3$ , то равенство выполнено, иначе $x> 1 3$ и $x+ 1< 3x ⇐⇒ x> 1 2$ .

Ответ:

$(0,1)∪(1,+∞ ) 3 2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#44156

Два мальчика в течение нескольких часов ходили кругами вокруг здания, оба по часовой стрелке, каждый с постоянной скоростью. Более быстрый проходил один круг за $5$ минут, более медленный — за некоторое целое число минут. При этом время между встречами тоже равнялось некоторому целому числу минут, причём оно было не меньше $12$ . За какое время более медленный мальчик проходил полный круг?

Источники: ПВГ-2016, 11.2 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1!

1) Воспользуемся частой идеей про задачи на круговое движение - выразим скорость их сближения через разность скоростей. Для этого нам понадобится время встречи, а еще время обхода круга каждым из них. Одно из них мы знаем, оставшиеся два неизвестных можем обозначить за t и t'.

Подсказка 2!

2) Итак, мы получим уравнение S/t = S/5 - S/t'. Заметим, что так как t' - целое, мы могли бы найти все подходящие t'!

Подсказка 3!

3) Для этого нужно сократить на S и получить несколько вариантов для t'. Останется только их разобрать!

Показать ответ и решение

Время между их встречами равно $t≥ 12$ , а время обхода круга для второго $t > 5 1$ . Запишем скорость сближения через разность их скоростей ( $S$ — длина круга)

S S S t-= 5 − t1 =⇒ 5t1 = (t1− 5)⋅t

Заметим, что $Н ОД(t1,t1− 5)∈{1,5}$ , потому $t1− 5∈{1,5,25}$ , чтобы $5t1$ было ему кратно. Если $t1− 5= 1,t1 = 6$ , то имеем $t= 30$ . Иначе $t1 ≥10$ . В этом случае первый хотя бы в два раза быстрее и время между встречами будет не более $10$ минут, поскольку за это время первый пройдёт два круга, а второй не более одного. Отсюда наш ответ единственный возможный.

Ответ:

$6$ минут

Ошибка.
Попробуйте повторить позже

Задача 8#44157

Для бригады маляров-учеников была запланирована окраска $360$ кв.м. стен. Перед началом работы один из учеников заболел, и вместо него работал мастер, производительность которого в $3$ раза больше производительности каждого из учеников. Поэтому каждый из учеников в действительности покрасил на $6$ кв.м. меньше, чем планировалось. Все ученики и мастер работали одинаковое время. Сколько учеников работало?

Источники: ПВГ 2016

Подсказки к задаче

Подсказка 1!

1) Давайте посмотрим, если всего учеников x, а покрасить надо было 360, то каждый должен был покрасить по 360/x, а покрасил 360/x - 6.

Подсказка 2!

2) Как бы нам записать, сколько покрасил мастер? Так как его производительность была в три раза больше, давайте считать, что добавление мастера это то же самое, что добавить трех учеников вместо одного! Попробуйте в таком случае записать уравнение на то, сколько в итоге было покрашено детьми и мастером!

Показать ответ и решение

Мастер работает в три раза быстрее, поэтому в суммарной производительности его можно считать за троих учеников.

Если всего учеников изначально было $n$ , то каждый планировал покрасить $360- n$ , а по факту покрасил $360 n − 6$ . Мастер красил вместе с ними как три ученика, а ещё один ученик заболел, поэтому суммарно они покрасили $(360 ) (n+ 3− 1)⋅ n − 6 =360$ . Осталось решить полученное уравнение

(60 ) (n+ 2) n-− 1 = 60

60+ 120− 2− n= 60 n

n2+ 2n− 120= 0

n =10

Изначально было $n =10$ учеников, но так как один заболел, то всего работало $9$ .

Ответ:

$9$

Ошибка.
Попробуйте повторить позже

Задача 9#51852

Серединами оснований $BC$ и $AD$ трапеции $ABCD$ являются точки $K$ и $L$ соответственно. Известно, что $AD = 10⋅BC.$ На боковых сторонах $AB$ и $CD$ взяты, соответственно, точки $M$ и $N$ , так что прямая $MN$ параллельна основаниям трапеции. При каком значении отношения $AM :MB$ сумма площадей треугольников $BKN$ и $MNL$ будет наибольшей?

Источники: ПВг-2016, 11.3 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Как можно перефразировать вопрос задачи?

Подсказка 2

Например, можно записать функцию суммы желаемых площадей и найти её наибольшее значение. Оно будет в точке максимума.

Подсказка 3

Пусть AD = k ⋅ BC (k > 1), BC = a, высота трапеции равна h, x = MB/AB, S(ABCD) = S. Выразите S(BKN) и S(MNL).

Подсказка 4

Можно воспользоваться тем, что у параболы с ветвями, направленными вниз, точка максимума находится в вершине.

Показать ответ и решение

Введем обозначения: $S = S,AD =k ⋅BC (k> 1),BC = a, ABCD$ высота трапеции $ABCD − h,x = MB. AB$ Тогда $S = a+kah, 2$ откуда $-2S ah= 1+k$ Получаем: $1 a -xS-- SBKN = 2 ⋅ 2 ⋅hx= 2(1+k).$ Так как $MN =x(k− 1)a +a,$ то

$PIC$

SMNL = a(x(k−-1)+-1)⋅(1− x)h= S(x(k-− 1)+-1)(1−-x) 2 1+ k SBKN +SMNL = ---S-- (2x2(1 − k)+ x(2k− 3)+2) 2(1+ k)

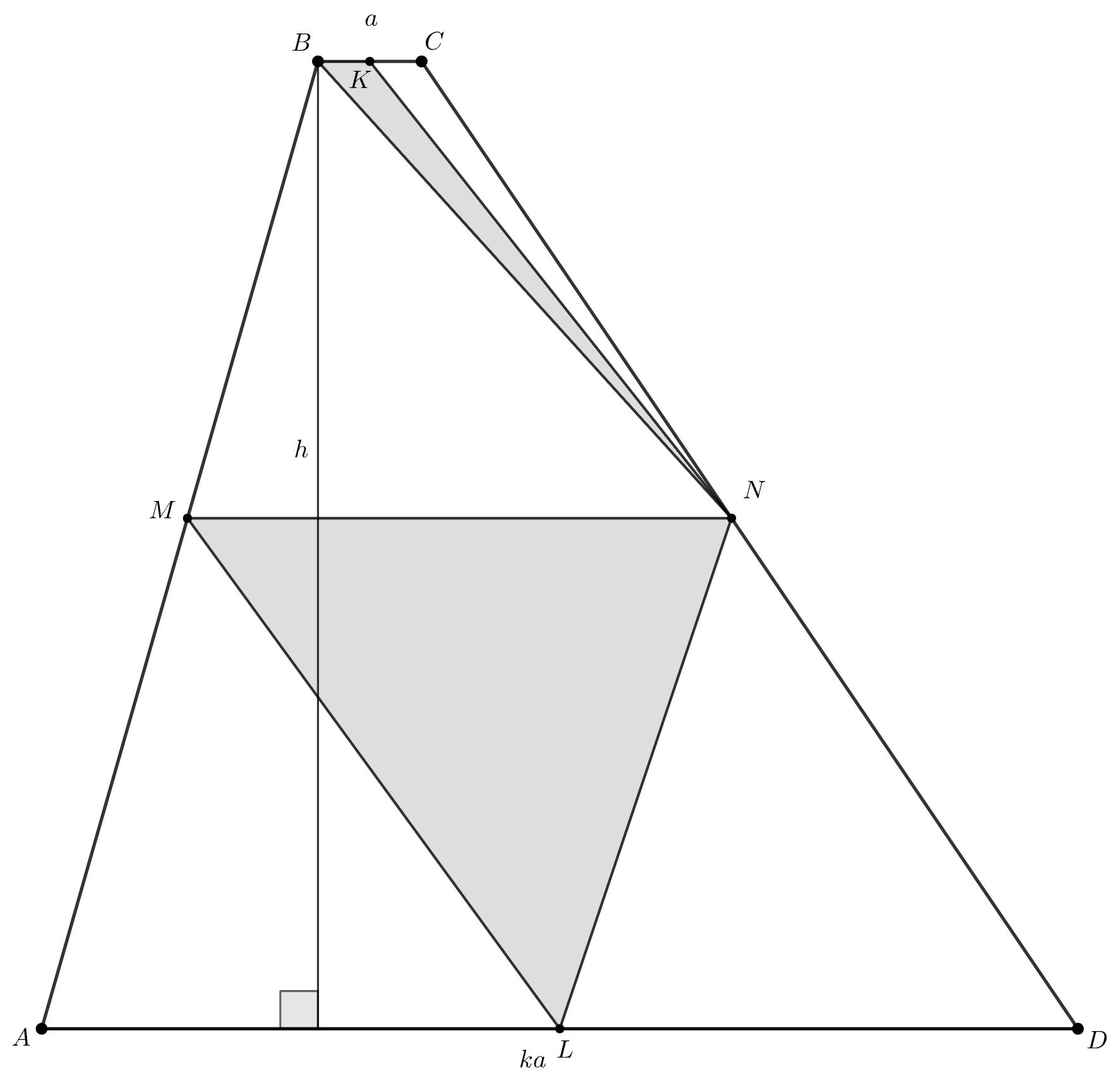
Функция $f(x)= 2x2(1− k)+x(2k− 3)+ 2$ имеет максимум при $x0 =-2k−-3 4(k− 1)$ Если $k= 10,$ то $x0 = 17, 36$ откуда $AM :MB =19 :17.$

Ответ:

$19:17$

Ошибка.
Попробуйте повторить позже

Задача 10#58562

Найдите значение выражения

( --3-- --2-- --1--) --y2--- 2x− y − 2x+ y − 2x− 5y :4x2− y2

при

x= 4,y = 7 3 3

Источники: ПВГ-2016, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Не теряемся и приводим к общему знаменателю, объединяем нужное, сокращаем ненужное, а затем в уже красивое выражение подставляем значения!

Показать ответ и решение

Приведём к общему знаменателю в скобках, получим

4x2-− y2-3(2x+-y)(2x− 5y)−-2(2x−-y)(2x−-5y)−-(2x-+y)(2x−-y) y2 ⋅ (4x2− y2)(2x − 5y) =

2 2 2 2 2 2 = 12x-−-24xy− 15y-−28x-+-24xy− 10y-−-4x-+y-=− --24---= −24= 8 y (2x− 5y) 2x− 5y −9 3

Ответ:

$8 3$

Ошибка.
Попробуйте повторить позже

Задача 11#61177

Найдите все четырёхзначные числа, которые на $7182$ меньше числа, записанного теми же цифрами в обратном порядке.

Источники: ПВГ 2016

Подсказки к задаче

Подсказка 1

Представим наше число в виде abcd, тогда в обратном порядке получится dcba. Расписываем числа через степени десятки и составляем уравнение по условию

Подсказка 2

Отлично, получилось 111(d-a) + 10(c-b) = 798. Понимая, что a, b, c, d - цифры, оценим слагаемые.

Подсказка 3

Заметим, что d-a при делении на 10 имеет остаток 8, причем a и d - первые цифры в числах, что приводит нас к единственному случаю, остается только счет)

Показать ответ и решение

Пусть это число $abcd= 1000a +100b+10c+ d$ , отсюда

(1000d +100c+10b+ a)− (1000a+ 100b+ 10c+d)= 999d+ 90c− 90b− 999a= 7182

Сокращая результат на $9$ , получаем

111d+ 10c− 10b− 111a= 111(d− a)+10(c− b)= 798

Поскольку $10(c− b)∈[−90,90]$ , то $111(d− a)∈ [708,888]$ , отсюда $111(d − a)∈ {777,888}.$

Добавляя условие, что $111(d− a)=798− 10(c− b) ≡8 10$ (то есть даёт остаток $8$ по модулю $10$ ), получаем единственный случай $d− a= 8,d= a+8.$

Поскольку $a⁄= 0$ , то остаётся $a= 1,d =9$ , отсюда

10(c − b)= 798− 888= −90 ⇐⇒ b=c +9 =⇒ c= 0,b= 9

Получаем единственное подходящее число $1909.$

Ответ:

$1909$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#63898

Двугранный угол при основании правильной треугольной пирамиды $SABC$ равен $arctg3.$ В каком отношении делит боковую сторону $SB$ сфера, центр которой лежит в плоскости основания, если известно, что вершины основания принадлежат сфере?

Источники: ПВГ 2016

Подсказки к задаче

Подсказка 1

Центр сферы лежит в плоскости основания и при этом сфера проходит через все вершины правильного треугольника основания. Что в таком случае можно сказать о положении центра сферы внутри △ABC?

Подсказка 2

Итак, мы поняли, что центр сферы совпадает с центром △ABC. Из этого мы сразу же можем узнать радиус сферы. Обозначьте сторону основания пирамиды за переменную а и попробуйте через неё выразить всё что сможете: радиус сферы, высоту пирамиды (в этом нам поможет двугранный угол при основании).

Подсказка 3

Обозначим центр сферы за точку О и рассмотрим △SOB, все его стороны легко выражаются через а. Из точки О проведите ОР — радиус сферы. Работа с равнобедренным △ВОР (мы знаем в нём боковые стороны и можем выразить из прямоугольного △SOB угол при основании) поможет нам отыскать ВР. Осталось несколько арифметических действий и задача решена!

Показать ответ и решение

$PIC$

Центр сферы равноудалён от точек на её поверхности, а раз по условию вершины основания принадлежат сфере, то центр сферы является центром описанной около основания окружности.

Пусть сфера пересекает ребро $SB$ в точке $P$ . Тогда равны радиусы $OP =OB.$ Опустим перпендикуляр $OQ$ к ребру $SB$ , он является медианой равнобедренного треугольника $P OB.$ Обозначим сторону основания через $a$ и пусть угол $α =arctg3.$ Пусть $M −$ основание перпендикуляра, проведенного из точки $B$ на сторону $AC.$

Находим из правильного треугольника в основании $√- √ - OM = 13a23,OB = 23a23$ , а так как $∠SMO$ это линейный угол двугранного угла и равен $α$ , то $√- SO = a63tgα.$

Также заметим

cos∠SBO = BQ- = BO BO SB

Тогда получаем

BQ- BO2- 2 -----1----- SB = SB2 = cos ∠SBO = 1+ tg2 ∠SBO =

(так как $√- a√3- tgα tg∠SBO =a 36tgα :-3-= -2-)$

1 4 4 = ---tg2α-= 4+tg2α-= 13- 1+ 4

В итоге $BQ =QP = 4x,SB = 13x,$ так что сфера делит в отношении

SP-= 13x−-8x= 5 PB 8x 8

Ответ:

$5 :8$

Ошибка.
Попробуйте повторить позже

Задача 13#67596

Решите уравнение

√- 2016 √ ----2016 ( x) + ( 1− x) = 1

Источники: ПВГ-2016 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Ключом к решению этой задачи является правильно написанное ОДЗ! Поэтому для начала найдем ОДЗ нашего уравнения!

Подсказка 2

Верно, 0 ≤ x ≤ 1! А что можно сказать про (√x)²⁰¹⁶ и (√(x-1))²⁰¹⁶? Может мы их можем как-то оценить, учитывая наше ОДЗ?

Подсказка 3

Да, если есть число, которое меньше единицы, но больше нуля, то при возведении в степень это число будет уменьшатся! То есть, мы имеем: x¹⁰⁰⁸ < x и (1-x)¹⁰⁰⁸ < 1 — x! Таким образом, если x ≠ 0 и x ≠ 1, то решений нет! Осталось проверить случаи x = 1 и x = 0.

Показать ответ и решение

ОДЗ: $0≤ x≤ 1.$

Подстановкой легко убедиться, что $x= 0$ и $x = 1$ — это решения.

При $0< x< 1$ (на оставшейся области ОДЗ) оценим слагаемые в левой части

{ √- 2016 0< x< 1 ⇐⇒ ( x)√ --<-x2016 0< 1− x< 1 ⇐⇒ ( 1− x) <1− x

Складывая эти неравенства, получаем

√- 2016 √ ----2016 ( x) + ( 1− x) < x+ (1 − x)= 1

Поэтому на интервале $(0;1)$ левая часть строго меньше единицы и равняться единице не может.

Ответ:

$0;1$

Ошибка.
Попробуйте повторить позже

Задача 14#70325

Найдите все пары натуральных чисел $(x,y)$ , для которых выполнено равенство

2 x +xy = y+ 92

Источники: ПВГ - 2016, 9 класс

Подсказки к задаче

Подсказка 1

Попробуйте преобразовать выражение.

Подсказка 2

Вычтите из обеих частей y+1.

Подсказка 3

Вспомните формулы сокращённого умножения.

Подсказка 4

Разложите 91 на простые множители.

Показать ответ и решение

Вычтем из обеих частей $y+ 1$ и разложим левую часть на скобки

x2+ xy = y+ 92⇔ x2+ xy− y − 1 =91⇔ x2− 1+ y(x − 1)= 91⇔ ⇔ (x− 1)(y+ x+ 1) =91= 7⋅13

Так как $x,y ∈ ℕ, y+ x+ 1> x− 1,$ а также обе скобки неотрицательны. Значит возможны только следующие случаи:

[ x− 1= 1 и y+x +1 =91 x− 1= 7 и y+x +1 =13

Решив систему уравнений в натуральных числах в каждом из случаев, получаем ответ.

Ответ:

$(2,88),(8,4)$

Ошибка.
Попробуйте повторить позже

Задача 15#70327

Найдите все натуральные числа $x$ и $y$ , удовлетворяющие уравнению

3 2 x +2y = 2016

Источники: ПВГ-2016, 11.1 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Как вообще стоит решать данную задачу? Можно ли тут, например, разложить что-либо на скобки?

Подсказка 2

Можно было бы перебрать все пары (x;y), но их много. Есть ли способ сократить перебор?

Подсказка 3

2016 делится на 2, что можно тогда сказать про x?

Подсказка 4

x должно быть четным, представьте x как 2k, где k — целое число.

Подсказка 5

Аналогичным образом можно преобразовать и y.

Показать ответ и решение

Получить хорошее разложение на скобки тут не получится, а перебор всех пар $(x,y)$ большой. Сократим его, воспользовавшись четностью:

. x.. 2⇒ x =2k, k ∈ℕ ⇒ ⇒ 8k3+ 2y2 = 2016⇔ 4k3+y2 =1008; y ... 2⇒ y =2n, n ∈ℕ ⇒ ⇒ 4k3 +4n2 = 1008 ⇔ k3+n2 =252.

Так как $73 = 343 >252,$ разберем 6 возможных значений $k$ и выберем те, при которых $n∈ ℕ.$

⌊ k= 1 и n2 = 251 || k= 2 и n2 = 244 ||| k= 3 и n2 = 225⇒ x= 6, y = 30 || k= 4 и n2 = 188 ||⌈ k= 5 и n2 = 127 k= 6 и n2 = 36⇒ x =12, y = 12

Ответ:

$(6,30),(12,12)$

Ошибка.
Попробуйте повторить позже

Задача 16#74216

Решите в целых числах уравнение

6 3 x =y + 217

Источники: ПВГ - 2016, 9 класс(см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Когда нужно решить уравнение в целых числах, какие у нас обычно есть варианты действий?

Подсказка 2

Выбрать нужно вариант, который максимально сократит количество переборов. Для этого нужно внимательно посмотреть на уравнение: можно ли его как-то удобно преобразовать?

Подсказка 3

Обратите внимание на степени х и у. Случайно, не возникает никаких ассоциаций?

Подсказка 4

Можно перенести y³ влево и воспользоваться разностью кубов. Тогда что можно сделать с числом справа?

Подсказка 5

Что нужно сделать с числом 217, чтобы понять, какие значения могут принимать множители слева?

Подсказка 6

Да, разложим его на множители — останется только перебрать варианты.

Подсказка 7

Число 1 тоже может быть множителем.

Подсказка 8

Вышло несколько вариантов систем уравнений, которые нужно решить? А что можно сделать, чтобы решить систему?

Подсказка 9

Выражаем у через х и подставляем во второе уравнение. Осталось только всё найти)

Показать ответ и решение

Запишем уравнение в виде $(x2− y)(x4+ x2y +y2)= 217.$ Осталось просто перебрать всевозможные варианты значений скобочек. Чтобы сократить перебор, заметим, что первая скобка меньше второй, а значит она меньше $√--- 217.$ Таким образом, возможны варианты $1,217$ и $7,31,$ так как вторая скобка всегда положительна, значит и первая должна быть положительна. Ясно, что в обоих случаях надо выразить $y$ через $x$ и подставить во второе уравнение, получится квадратное уравнение, которое нужно решить и выписать целочисленных ответы ответы.

Ответ:

$(±3,8),(±1,− 6)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#90131

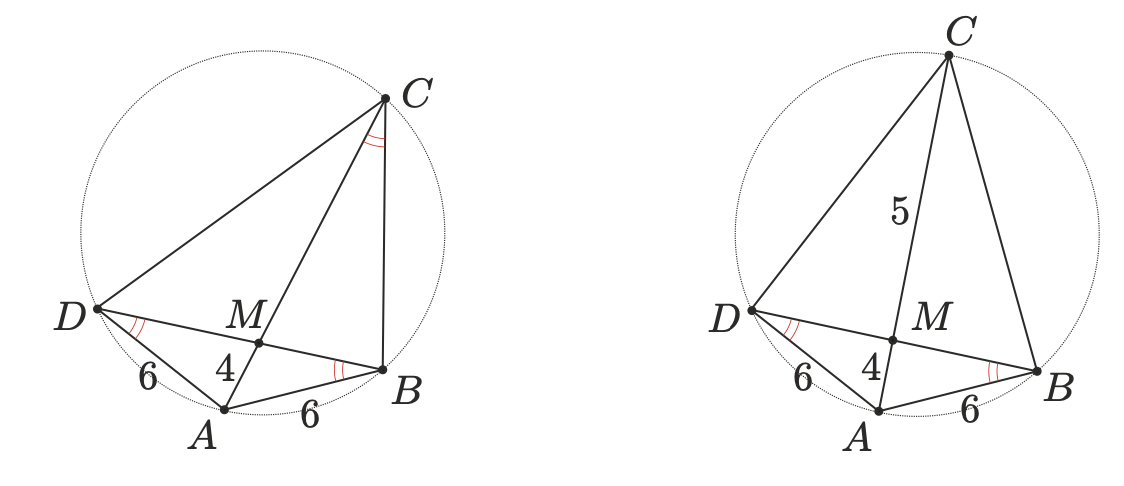
В окружность с центром $O$ вписан четырехугольник $ABCD$ , диагонали $AC$ и $BD$ которого пересекаются в точке $M$ , причем $AM =4,AB = 6$ . Определите, какой может быть наименьшая длина диагонали $BD$ , если известно, что стороны $AB$ и $AD$ равноудалены от точки $O$ .

Источники: ПВГ 2016

Подсказки к задаче

Подсказка 1

Какой вывод можно сделать из равноудаленности AB и AD от точки O?

Подсказка 2

Они равны! А что вытекает из равенства хорд в окружности?

Подсказка 3

Углы ACD, ADB, ABD равны! Не возникло ли где у нас подобия? Быть может, можно посчитать еще какие-то отрезки?

Подсказка 4

Треугольники ABM и ACB подобны! Отсюда можно посчитать какие-нибудь отрезки. Теперь попробуем подступиться к отрезкам на DB. Быть может, попробуем их выразить при помощи свойства отрезков на пересекающихся хордах?

Подсказка 5

DM * MB = CM * MA = 5*4, что есть DM = 5x, MB = 4/x. Осталось лишь минимизировать сумму ;)

Показать ответ и решение

Из равноудалённости сторон $AB$ и $AD$ от точки $O$ вытекает их равенство. Следовательно равны углы $∠ACD = ∠ADB = ∠ABD$ . Таким образом, треугольники $ABM$ и $ACB$ подобны. Откуда $2 AB = AM ⋅AC$ , т.e. $AC = 9$ , а следовательно, $MC = 5$ . Так как $DM ⋅MB = CM ⋅MA = 5⋅4$ , то $DM = 5x,MB = 4∕x.$ Следовательно,

4 ( 4) 2 √ - BD = 5x+ x = 5 x + 5x ≥ 5⋅2⋅√5-=4 5,

применяя $a2+ b2 ≥2ab$ . Остаётся заметить, что данный случай реализуется, когда $AC$ проходит через центр окружности.

$PIC$

Ответ:

$4√5$

Ошибка.
Попробуйте повторить позже

Задача 18#90802

Укажите все значения параметра $a$ , при каждом из которых система

{ x2+ 2y2+2y(x− a)+ a2 = 0 2−2−y⋅log x <1 2

имеет решения, и найдите эти решения.

Источники: ПВГ 2016

Подсказки к задаче

Подсказка 1

Внимательно рассмотрите первое уравнения, можно ли его красиво преобразовать? Аккуратная работа с ФСУ позволит нам установить соотношения между х, у и а.

Подсказка 2

Итак, подставляя полученные соотношения, мы получаем интересное неравенство, но как его решить? Попробуйте показательную функцию отправить в правую часть, а логарифм — в левую. Что можно сказать о полученном неравенстве?

Подсказка 3

Оцените возрастание/убывание функций с каждой стороны, чтобы сделать вывод о количестве пересечений и примерном виде графиков этих функций. Так мы получим решения для х.

Подсказка 4

Осталось воспользоваться найденными в начале соотношениями между х и а, чтобы установить искомые значения параметра!

Показать ответ и решение

ОДЗ: $x> 0.$

Из первого уравнения имеем $2 2 (x+ y) +(y− a)= 0⇒ x= −y, y = a.$ Подставим в неравенство:

−2+x 2 ⋅log2x< 1

x 2 log2x< 4

Поскольку функция в левой части монотонно возрастает, то меньше 4 она будет при всех $x$ до момента равенства. А равенство $2xlog2x =4$ достигается при $x = 2.$

В итоге с учётом ОДЗ $x∈ (0;2)$ , откуда $a∈ (− 2;0)$ , причём для каждого значения существует ровно одна пара $(x,y)= (−a,a).$

Ответ:

$a ∈(−2;0), (x,y)= (−a,a)$

Ошибка.
Попробуйте повторить позже

Задача 19#91545

Решите неравенство

√ -------- 3 3 2sinxcosx> cos x− sin x+ sinxcosx(sin x− cosx)

Источники: ПВГ - 2016, 10-11 классы, Уфа

Подсказки к задаче

Подсказка 1

Вспомните формулы сокращённого умножения.

Подсказка 2

Выражение в правой части сворачивается до cos(x) - sin(x).

Подсказка 3

Что, если правая часть меньше нуля?

Подсказка 4

В противном случае, можем возвести в квадрат.

Показать ответ и решение

Правая часть неравенства по формуле разности кубов равна

2 2 (cosx − sin x)(cos x+ sinxcosx+ sin x)− sin xcosx(cosx− sinx)=

2 2 =(cosx− sin x)(cos x+ sin x)= cosx− sinx

Поэтому получаем неравенство

∘sin(2x)> cosx− sinx

Если правая часть меньше нуля, то неравенство выполнено на ОДЗ $sin(2x) ≥0.$

[ π4 + 2πk< x≤ π2 +2πk,k∈ ℤ π+ 2πk≤ x< 54π+ 2πk,k∈ ℤ

Если правая часть неотрицательна, то неравенство равносильно

sin(2x)> (cosx− sinx)2

sin(2x)> 12

[ π12 + 2πk< x≤ π4 + 2πk,k ∈ℤ 5π4 + 2πk≤ x< 117π2-+2πk,k∈ ℤ

Объединяя эти два случая, получаем ответ.

Ответ:

$(π-+ 2πk;π +2πk]∪[π+ 2πk;17π+ 2πk);k∈ ℤ 12 2 12$

Ошибка.
Попробуйте повторить позже

Задача 20#92005

Найдите минимальное значение выражения

∘ -----2---2 ∘ -2-------2 (x+ 6) + y + x + (y − 4)

при условии $2|x|+ 3|y|= 6$ .

Источники: ПВГ 2016

Подсказки к задаче

Подсказка 1

Давайте подумаем, а в каких формулах нам встречались похожие выражение? Сумма квадратов по корнем...

Подсказка 2

Что-то похожее на условия нам встречалось в формуле нахождения расстояния от точки до точки! Осталось лишь понять, от какой и до какой ;)

Подсказка 3

Выражение из условия есть сумма расстояний от точки (x,y) до (-6, 0) и (0, 4). Теперь нам надо подумать, а где же лежит точка (x, y)? Что "рисует" второе выражение из условия? ;)

Подсказка 4

Второе выражение из условия есть ромб с центром в начале координат! Получается, нам нужно минимизировать сумму расстояний от точки на стороне ромб до двух фиксированных!

Подсказка 5

Попробуем воспользоваться идеей симметрии, чтобы найти подходящую точку ;)

Подсказка 6

Докажите, что нам подходит точка, равноудаленая от двух фиксированных!

Показать ответ и решение

Заметим, что выражение из условия есть сумма расстояний от точки с координатами $(x,y)$ до точек $(−6,0)$ и $(0,4)$ . А уравнение $2|x|+ 3|y|= 6$ задаёт ромб. Наша задача свелась к нахождению точки на границе ромба с минимальной суммой расстояний до двух выбранных. Докажем, что этот минимум достигается в точке, равноудаленной от точек $(−6,0)$ и $(0,4)$ .

Пусть точка $G$ лежит на прямой $l$ , параллельной $EF$ , и удаленной от прямой $EF$ на расстояние $h$ . Пусть также точка $H$ на прямой $l$ такова, что $EH =FH$ , а точка $P$ симметрична $F$ относительно прямой $l$ . Тогда получаем

EG + FG ≥EH + HP = EH + HF.

Причем равенство получается только, если точки $G$ и $H$ совпадают.

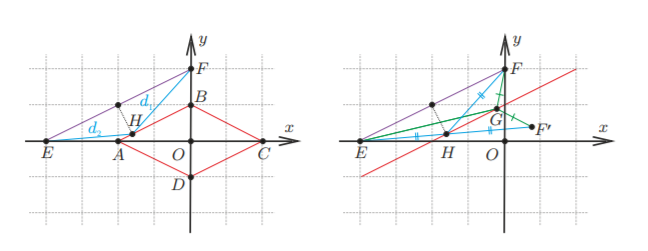
В нашем случае сторона ромба $AB$ параллельна $EF$ , а точка $H$ на прямой $AB$ , для которой $EH = FH$ , лежит на стороне ромба. Сумма расстояний от любой другой точки ромба до точек $E$ и $F$ больше $EH + FH$ . Остается найти $EF$ и расстояние между прямыми $EF$ и $AB$ . Применяя теорему Пифагора, получаем $√ ------ √-- EF = 16+36= 2 13$ . Расстояние между прямыми равно расстоянию от прямой $AB$ до начала координат, поэтому

h⋅AB = AO⋅BO,

откуда $h =√6-- 13$ .

Таким образом,

∘ 36---- ∘205 EH + FH =2 13 + 13= 2-13

Ответ:

$2∘ 205 13$