ПВГ 2012
Ошибка.
Попробуйте повторить позже
В окружности диаметр и хорда
пересекаются в точке
под прямым углом. Найдите длину биссектрис треугольника
если
,
Источники:
Подсказка 1
По сути, всё, что у нас сейчас есть на картинке — это два прямоугольных подобных треугольника PAC и QCB, у которых известная одна сторона, а также есть равенство из того, что это пересекающиеся хорды в окружности. Вы скажете, что это одно и тоже, но плюс в том, что у нас ещё появляется отношение AP к QB, которые, в свою очередь, удачно выражаются через стороны треугольника, хорды ведь пересекаются под прямым углом. Попробуйте применить рассуждения выше к тому, чтобы выразить все отрезки через некоторый в этой задаче (мы же поняли, что она счётная на подобия, поскольку у нас в условии есть только окружность и хорды).
Подсказка 2
Удобным здесь будет взять за х отрезок BC, поскольку именно он меньше в 8 раз отрезка AC. Тогда, чтобы выразить все отрезки хорд, остается лишь записать равенство на произведение отрезков хорд (или, говоря умными словами, расписать степень точки C относительно нашей окружности).
Подсказка 3
В силу наличия отношения уже указанных сторон, связанного с подобием, у нас есть равенство на х, откуда он находится. Значит, мы нашли все отрезки хорд и картинка фиксирована. Значит, мы можем найти все отрезки треугольника из условия. Остается только вспомнить формулу биссектрисы и факт про отношения на которые разбивает биссектриса сторону, и задача решена!
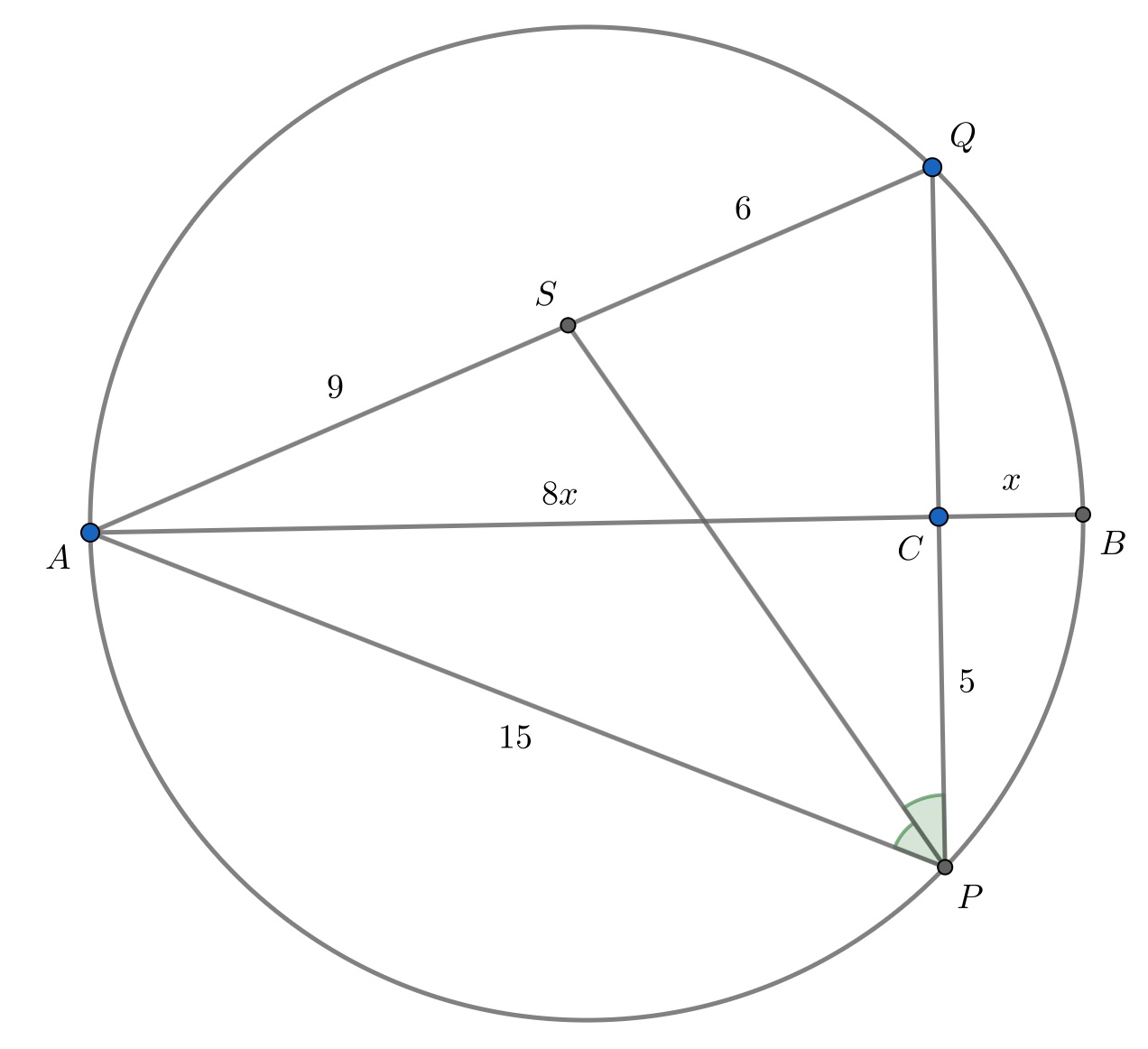
Обозначим тогда
и из
получаем, что
Поскольку
равнобедренный, то
биссектриса угла
и
По теореме Пифагора
Пусть биссектриса угла
пересекает
в точке
Taк как
то по свойству биссектрисы получаем:
Из
по
теореме косинусов получаем, что
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




