Тема Ломоносов - задания по годам

Ломоносов 2014

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ломоносов - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#39869Максимум баллов за задание: 7

Найдите все пары $(a,b)$ , при которых множество решений неравенства $log (x− a)> 2014$ $2x2− x− b$ совпадает с промежутком $(0;1)$ .

Источники: Ломоносов-2014, 11.4 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

В этом неравенстве есть и логарифм, и квадратичная функция... Стандартными способами такое не решишь( Обычно в таких случаях стоит подумать про какие-нибудь свойства функций, например, монотонность, чётность, выпуклость и т.д. Может, что-нибудь из этого набора нам поможет?

Подсказка 2

Монотонность у логарифма есть, но у квадратичной функции её нет. Чётность тоже не прослеживается... А вот что насчёт выпуклости? Логарифм в этом неравенстве — это выпуклая вверх функция, а вот квадратичная функция тут выпукла вниз. А нам нужно, чтобы график логарифма лежал выше параболы на целом отрезке (0; 1)... Что для этого достаточно и необходимо?

Подсказка 3

Ну конечно, график логарифма должен пересекать параболу в двух точках — в 0 и 1! Других точек пересечения быть не может в силу выпуклости. Что теперь мы можем сделать?

Подсказка 4

Да, просто приравниваем левую и правую части неравенства, решениями этого уравнения должны быть x = 0 и x = 1. Осталось решить получившуюся систему!

Показать ответ и решение

Заметим, что $f(x)= 2x2− x − b− log (x− a) 2014$ имеет не более двух корней, поскольку её вторая производная всегда положительна. Если $x =1$ не входит в ОДЗ, то $x< 1$ не могут быть решениями, потому возможны два случая

$x =0$ не входит в ОДЗ, тогда $a= 0$ , потому что ОДЗ $x> a$ , а любой $x > 0$ лежит в решениях, но не $x =0$ . Тогда при $x =1$ достигается равенство, поскольку функции с обеих сторон непрерывны (иначе единица также входила бы в решение)
$log20141= 2− 1− b ⇐ ⇒ b =1$
Если $x → 0$ , то логарифм стремится к $− ∞$ , тогда как в левой части в пределе будет $− 1$ , тогда нужное неравенство не выполняется и этот случай нам не подходит.
$x =0$ входит в ОДЗ и $a <0$ . В этом случае решениями являются оба конца промежутка
${ log (−a)= −b { −a= 2014−b { b= log 2013 log2014(1− a)= 1− b ⇐ ⇒ 1− a =20141−b =− 2014a ⇐⇒ a =− 20114 2014 2013$
Поскольку $f$ имеет положительную вторую производную и непрерывна, то отрицательна она только на промежутке между этими корнями (на бесконечности она положительна, как и при $x→ a$ ), то есть найденные значения подойдут.

Ответ:

$(− -1-,log 2013) 2013 2014$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#48589Максимум баллов за задание: 7

Маша выписала на доске подряд все натуральные числа от $2$ до $2015.$ Пришёл Ваня и заменил каждое из этих чисел суммой его цифр. Пришла Таня и сделала то же самое с получившимися числами. Так продолжалось до тех пор, пока на доске не осталось $2014$ однозначных чисел (цифр). Какова сумма всех оставшихся чисел?

Источники: Ломоносов-2014, 11.2 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Хмм… В задаче фигурирует число и его сумма цифр… А что мы знаем про число и его сумму цифр?

Подсказка 2

Верно! Что они сравнимы по модулю 9. То есть если мы возьмем число, а потом заменим его, на его сумму цифр, то остаток mod 9 не поменяется. А если еще раз так сделаем? А еще? Что тогда в конечном итоге останется от изначального числа?

Подсказка 3

Да, останется остаток числа при делении на 9. Для всех чисел. Остается теперь правильно посчитать сумму остатков чисел от 2 до 2015 и задача решена!

Показать ответ и решение

Первое решение.

При взятии суммы цифр не меняется остаток при делении числа на $9$ . Поскольку все выписанные числа были положительными, то $0$ получиться не может и если число было кратно $9$ , то вместо него останется цифра $9$ . Поэтому остаётся посчитать количество остатков каждого вида.

Заметим, что $2016$ кратно $9$ , $2016 9 = 224$ , тогда если взять числа от $1$ , до $2016$ , то получится $224$ подряд набора вида ${1,2,...9}$ , сумма всех полученных чисел будет равна $45⋅224.$ Но мы не брали числа $1$ и $2016$ , потому нужно вычесть из суммы $10$ , откуда и получаем ответ $45⋅224− 10 =10070.$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Число $a$ и сумма цифр числа $a$ при делении на 9 дают одинаковые остатки, поэтому в итоге на доске останется ряд чисел: $2,3,4,5,6,7,8,9,1,2,...,9,1$ , 2 , и так далее. Так как $2014 =9 ⋅223+ 7$ , то в этом ряду 223 раза встретится последовательность от 1 до 9 и будет ещё 7 цифр. Значит, ряд заканчивается цифрой 8, и искомая сумма чисел равна

(1+ 2+ ...+ 9)⋅224− 1− 9 =45⋅224− 10 =10070

Ответ:

$10070$

Ошибка.
Попробуйте повторить позже

Задача 3#63895Максимум баллов за задание: 7

В правильную треугольную призму $ABCA B C 1 1 1$ вписан шар радиуса $√2$ . Найдите площадь боковой поверхности вписанного в шар прямого кругового цилиндра, основание которого лежит в плоскости, проходящей через точку $A$ и середины рёбер $BB1$ и $CC1.$

Источники: Ломоносов-2014, 11.7 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте аккуратно нарисуем рисунок, попробуем выразить радиус основания цилиндра через его высоту и радиус сферы. Обозначим за D, D₁, M и N середины ребер ВС, В₁С₁, ВВ₁ и СС₁, Р – точка пересечения MN и DD₁. Как имеющиеся на рисунке отрезки связаны с радиусом сферы?

Подсказка 2

Давайте спроецируем центр сферы на плоскость основания цилиндра, нельзя ли теперь выделить на рисунке какую-нибудь пару подобных треугольников, которая поможет нам связать высоту цилиндра и радиус сферы?

Показать ответ и решение

Обозначим через $r$ радиус шара, а через $D,D ,M 1$ и $N$ — середины рёбер $BC,B C ,BB 11 1$ и $CC 1$ соответственно. Плоскость $AA D 1 1$ есть центральное сечение шара. Пусть $h$ — высота цилиндра, тогда радиус его основания равен $∘ -2--h2- R = r − 4$ . Пусть $P$ — точка пересечения отрезков $DD1$ и $MN$ .

$PIC$

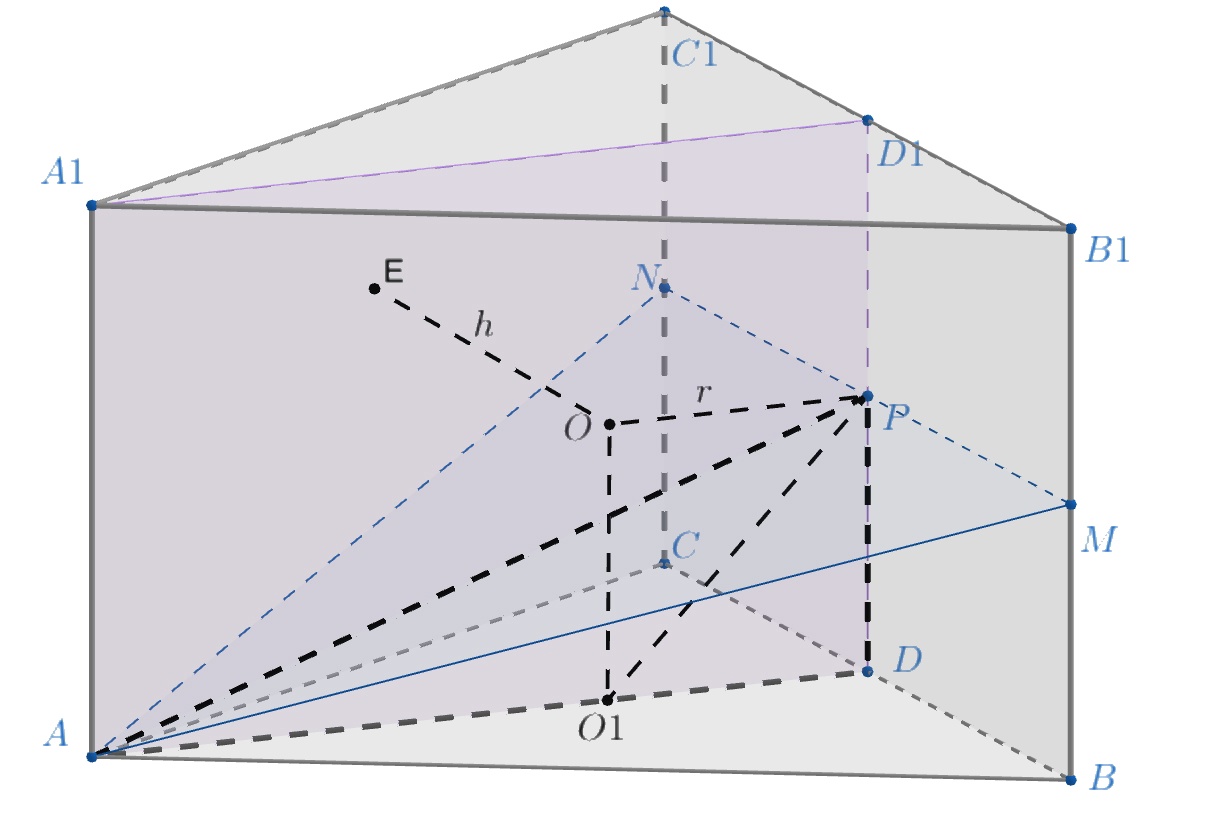
Справедливы соотношения $OP = r,PD = r,AD = 3r$ , где $O$ — центр шара. Если $O1$ — проекция точки $O$ на основание цилиндра, то из подобия прямоугольных треугольников $AP D$ и $OO1P$ получаем

OO PD -OP1= AP-

OO1-= √--r2--2-= √1- r 9r + r 10

Тогда

r√10- r√10 OO1 = 10 ,h =2 ⋅OO1 = 5

Значит, $3r√10 R= 10$ . Площадь боковой поверхности

6πr2 Sбок. = 2πRh= 5

Ответ:

$12π 5$

Ошибка.
Попробуйте повторить позже

Задача 4#73402Максимум баллов за задание: 7

Прямоугольная таблица состоит из $5681$ одинаковых клеток. Петя и Вася пронумеровали клетки натуральными числами $1,2,...,5681$ подряд. Петя нумеровал клетки по строкам слева направо (сначала первую строку, затем вторую и т. д.), а Вася по столбцам сверху вниз (сначала первый столбец, затем второй и т. д.). Оказалось, что ровно в $5$ клетках их номера совпали. Чему равна сумма числа строк и числа столбцов в этой таблице?

Подсказки к задаче

Подсказка 1

Пусть было m строк и n столбцов. Пусть клетка, получившая одинаковые номера, находится в строке с номером i и столбце с номером j. Какое число в ней стоит?

Подсказка 2

Можно вычислить это число по столбцам и по строкам.

Подсказка 3

Полученное выражение можно привести к равенству двух произведений.

Подсказка 4

Подумайте, как нам может помочь НОД.

Подсказка 5

Разложите 5681 на простые множители.

Подсказка 6

При переборе вариантов можете посмотреть на остатки по модулю 4.

Показать ответ и решение

Пусть в таблице $m$ строк и $n$ столбцов, а клетка, получившая одинаковые номера, расположена в строке с номером $i$ и в столбце с номером $j.$ Тогда, если считать по строкам, в этой клетке стоит число $(i− 1)n+ j,$ а если считать по столбцам, то это $(j− 1)m +i.$ Следовательно, $(i− 1)n+ j = (j− 1)m+ i,$ что равносильно $(i− 1)(n− 1) =(j− 1)(m− 1).$

Если $m =1$ или $n= 1,$ то номера Пети и Васи совпадут во всех клетках. Значит, $m > 1$ и $n> 1.$ Пусть $d= (m − 1,n − 1),$ тогда $n − 1= pd,m− 1= qd,$ где $(p,q)=1.$ Получаем $(i− 1)p= (j− 1)q.$ Поэтому $i− 1= kq,j− 1= kp,k =0,1,...,d,$ так как $j − 1≤ n− 1= pd,$ аналогично с $i− 1.$ Следовательно, количество клеток, получивших одинаковые номера, равно $d+ 1= (n− 1,m − 1)+ 1.$

Так как $5681 =13⋅19⋅23,$ то $n= 13,m = 19⋅23=437$ или, наоборот, $n= 437,m = 13$ (чтобы убедиться, что других вариантов нет, достаточно перебрать остатки по модулю 4). В любом случае, $m + n= 450.$

Ответ:

$450$