Ломоносов до 2010
Ошибка.
Попробуйте повторить позже
Точки 
и 
лежат на одной прямой. Отрезок 
является диаметром первой окружности, а отрезок 
— диаметром второй
окружности. Прямая, проходящая через точку 
пересекает первую окружность в точке 
и касается второй окружности в точке
, 
Найдите радиусы окружностей.
Возможны три случая расположения точек 
и 
на прямой.
1. Точка 
лежит между точками 
и С. Тогда 
находится внутри второй окружности и не существует прямой, проходящей через
и касающейся второй окружности.
2. Точка 
лежит между точками 
и 
.
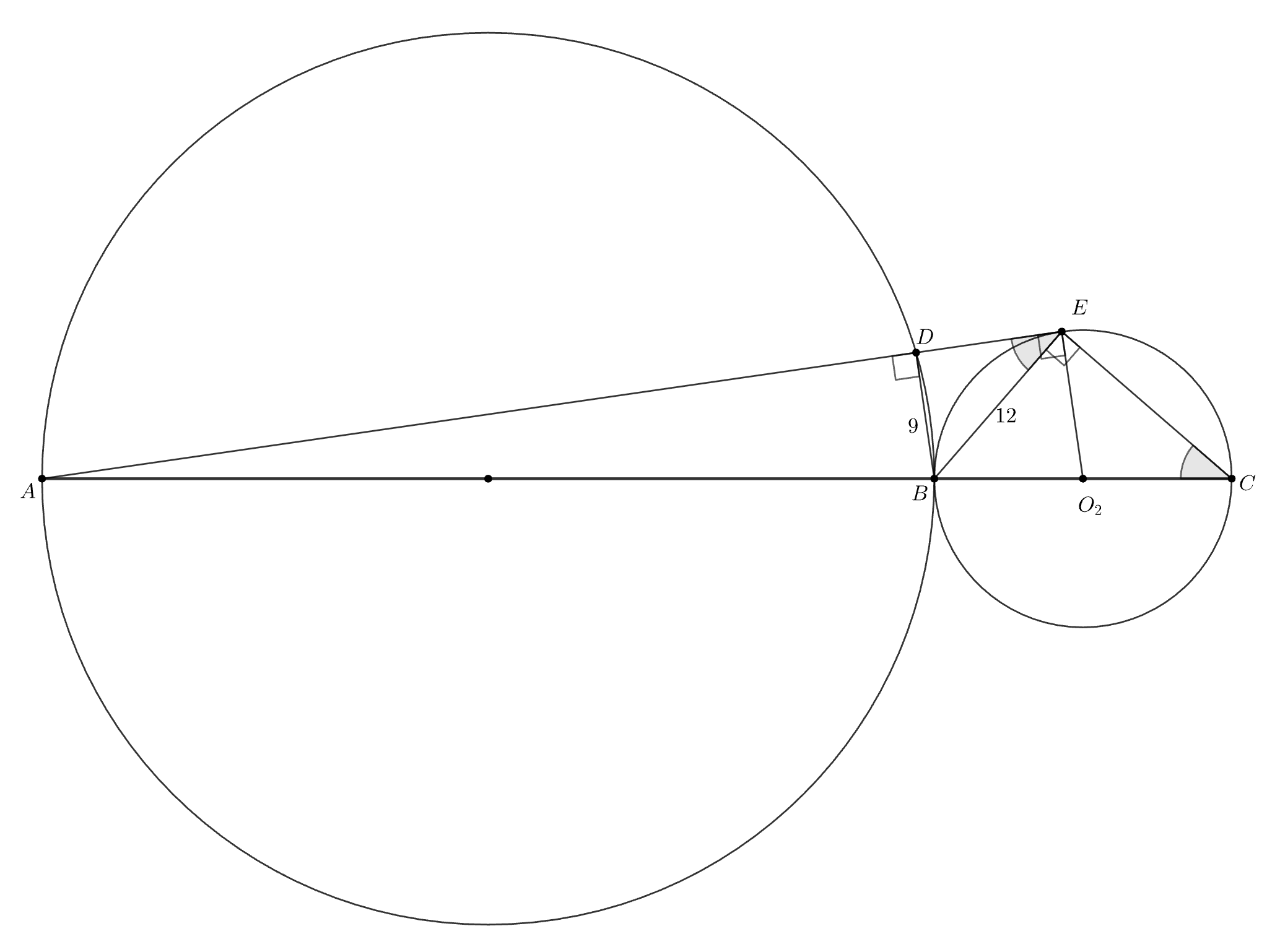
Имеем 
и 
как угол между касательной и хордой, равен 
Треугольники ВЕС и 
подобны по двум углам, откуда следует, что
Отрезки 
и 
параллельны, и должно выполняться неравенство 
а в то же время 
и 
так
что этот случай невозможен.
3. Точка 
лежит между точками 
и 
.
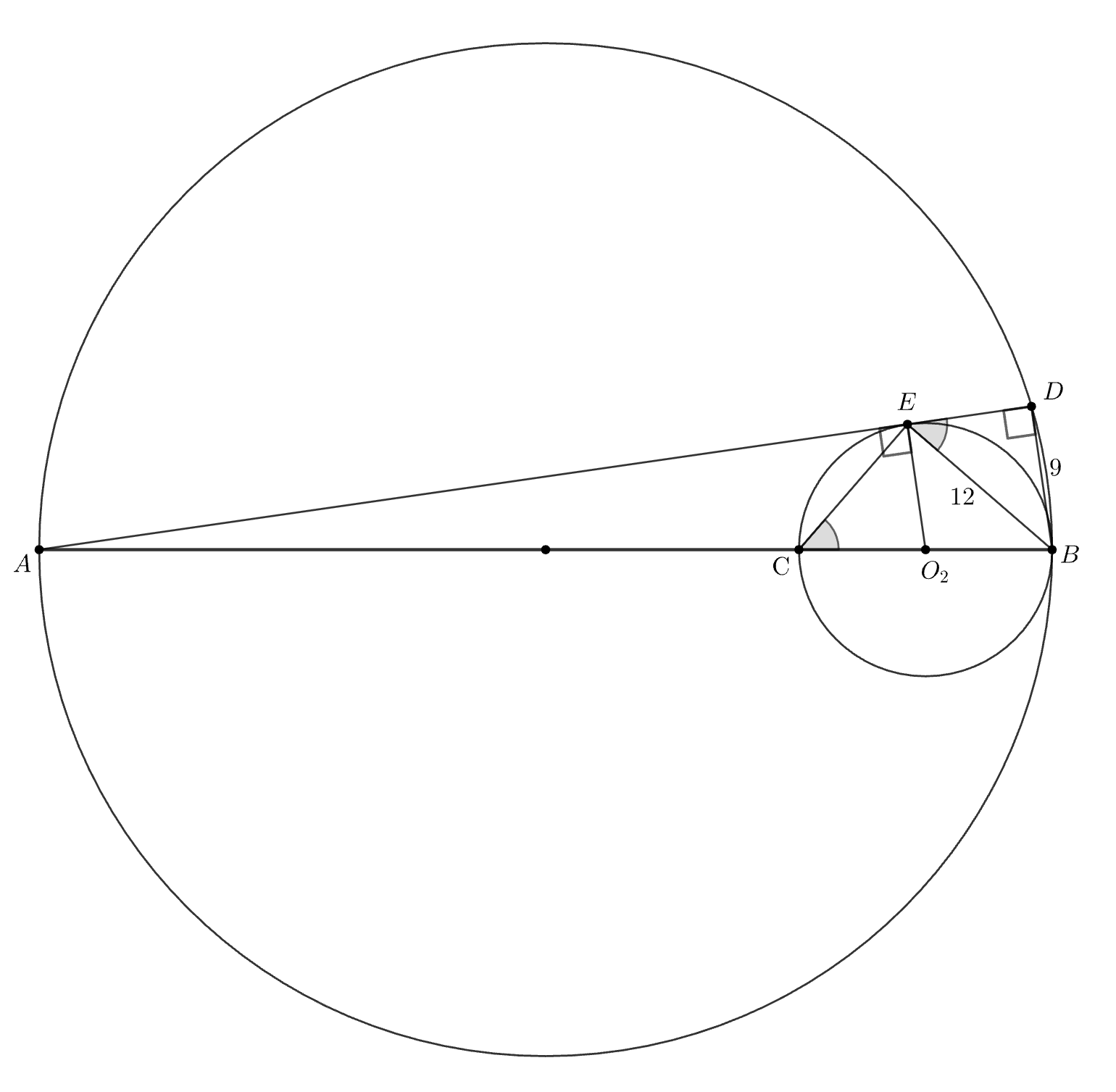
Дословно повторяя рассуждение из предыдущего случая, снова получаем 
Треугольники 
и 
также подобны по
двум углам, откуда следует, что
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
