Курчатов 2020
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На доске написаны числа т. е. все простые числа, не превосходящие
За одну операцию можно заменить
два числа
на максимальное простое число, не превосходящее
После нескольких операций на доске осталось одно число.
Какое максимальное значение оно может принимать?
Источники:
Подсказка 1
Если бы ответ был бы огромным, его было бы очень сложно искать(и проверять большие числа на простоту). Поэтому попробуем найти ответ среди тех, что уже записаны. Допустим, мы сделали одну операцию. Что можно сказать про новое число. Как можно его ограничить?
Подсказка 2
Оно лежит между числами, которые заменили на него. Тогда становится ясно, что 2017 не получить. А что получить можно и как?
Подсказка 3
Попробуем получить 2011. Работать с неизвестными нам простыми числами во второй тысяче сложно, поэтому попробуем найти алгоритм, которому не нужно точно описывать работу с ними. Как числа хотим оставить в конце для получения 2011?
по теореме косинусов это длина стороны напротив угла в
в треугольнике, поэтому она является средней из трёх сторон.
В связи с этим число
получиться не может, потому что каждое полученное в результате данной операции простое будет меньше
Поэтому наибольшее число, которое мы теоретически можем получить, это
Теперь приведём алгоритм, как получить 2011: будем последовательно выбирать два наибольших простых числа из всех, игнорируя
Так всегда будет оставаться меньшее из этих чисел, поскольку большее остаться не может, при этом на каждом шаге мы
рассматриваем два последовательных простых (это доказывается по индукции, поскольку на первом шаге мы оставим
из пары
и
и так далее). То есть на каждом шаге
при этом
— последовательные простые, поэтому между ними
других простых нет и мы будем выбирать
Наконец, останутся числа для них покажем, что
подходит:
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
Можно чисто алгебраически доказать неравенство при условии
Для этого достаточно возвести его
в квадрат и использовать
откуда сразу же получаем требуемое
Ошибка.
Попробуйте повторить позже
В Курчатовской школе за каждой партой сидит ровно 2 человека. Известно, что ровно у мальчиков сосед по парте – мальчик, а ровно
у
девочек – девочка. Во сколько раз мальчиков больше чем девочек?
Источники:
Подсказка 1
Мы знаем, какой процент мальчиков сидит за одной партой с мальчиком. Тогда сколько мальчиков сидит с девочкой?
Подсказка 2
Верно, 30%. Аналогично, 60% девочек сидит с мальчиками. Пусть количество мальчиков x, а девочек — y. Выразите через эти переменные количество мальчиков, сидящих с девочками, и количество девочек, сидящих с мальчиками. Что можно сказать про эти числа?
Подсказка 3
Верно, они равны! Теперь можно преобразовать равенство и найти ответ!
Пусть количество мальчиков , а девочек –
. Заметим, что
мальчиков сидит за партами с девочками и
девочек сидят за
партами с мальчиками. Так как за каждой партой сидит ровно 2 человека, то
, откуда
Таким образом, мальчиков в 2
раза больше, чем девочек.
Ошибка.
Попробуйте повторить позже
Найдите количество способов раскрасить все натуральные числа от 1 до 20 в синий и красный цвета так, чтобы оба цвета встречались и произведение всех красных чисел было взаимно просто с произведением всех синих чисел.
Источники:
Подсказка 1
Что можно сказать про числа из нашего набора, имеющие общий простой множитель?
Подсказка 2
Верно, они должны быть покрашены в один цвет! Тогда подумаем про раскраску чётных чисел.
Подсказка 3
Да, они будут одного цвета! Но тогда в эту же группу попадут числа, имеющие общий простой множитель с кем-то из чётных. Что это за числа?
Подсказка 4
Это числа, кратные трём, пяти, семи. Осталось совсем немного чисел, и теперь нужно понять, как будут раскрашены они:)
Заметим, что все чётные числа должны быть одного цвета. Так как среди них содержатся числа 6, 10 и 14, то числа, кратные 3, 5
и 7 должны быть того же цвета. Остались числа и 19. Заметим, что их можно распределить как угодно по
двум цветам. Таким образом, у нас есть 6 групп, каждая из которых может быть любого цвета, т. е. всего
способов
раскраски. Заметим, что из них не подходят 2 варианта, в которых все числа одного цвета, Итого получается
способа.
Ошибка.
Попробуйте повторить позже
Докажите, что при натуральном числа от 1 до
можно разбить на два множества так, чтобы произведения чисел в множествах
отличались не более чем в
раз.
Источники:
Подсказка 1
В задаче фигурирует n, поэтому можно было бы попробовать решать по индукции и аккуратно добавлять по числу. Какие трудности могут возникнуть в таком подходе? Как его скорректировать, чтобы было больше свободы в распределении чисел?
Подсказка 2
Можно вести индукцию с шагом 2. Тогда какие числа хочется добавить в каждое из множеств при доказательстве перехода?
Подсказка 3
Добавим n+2 в множество с меньшим произведением, а n+1 с большим произведением! Но нужно доказать, что оба частных меньше нужной нам дроби ;)
Докажем это утверждение индукцией по .
_________________________________________________________________________________________________________________________________________________________________________________
База при .
При разобьём на множества
и
, отношение равно
, что меньше
.
При разобьём на множества
и
. Отношение будет
, что как раз равно
.
При разобьём на множества
и
. Отношение равно
, что меньше
.
_________________________________________________________________________________________________________________________________________________________________________________
Переход индукиии от к
при
.
Пусть у нас есть разбиение чисел от 1 до , удовлетворяющее условию. Добавим в множество с меньшим произведением
число
, а в множество с бОльшим произведением
число
. Докажем, что произведения отличаются не более чем в
раз.
Так как , то
С другой стороны, так как , то
Докажем, что это не больше . Это равносильно
что верно при . Таким образом, переход доказан.
Ошибка.
Попробуйте повторить позже
Пусть — правильная четырёхугольная пирамида с основанием
На отрезке
нашлась точка
такая, что
и плоскости
и
перпендикулярны. Найдите отношение
.
Источники:
Подсказка 1
У нас точка M равноудалена от точек A и B. Быть может, попробуем найти ещё такие точки? Какое дополнительное построение может помочь найти все такие точки?
Подсказка 2
Постройте сечение плоскостью, являющейся серединным перпендикуляром к SB. Заодно и середину R у SB отметим, вдруг пригодится;) Какие точки и прямые туда попадут?
Подсказка 3
Именно, AC полностью лежит в построенной плоскости! Значит, теперь нам удобно работать со многими интересными треугольниками, которые лежат в этой же плоскости. Нам нужно найти некоторое отношение на AC, никаких длин нам не дано, поэтому имеем право обозначить AO за 1. Какие тогда отрезки мы можем посчитать?
Подсказка 4
AO = SO = 1, а OR — медиана в прямоугольном треугольнике, значит, можем посчитать и её ;) а что ещё можно сказать про R? в каких плоскостях она лежит, что примечательного есть в них?
Подсказка 5
RM перпендикулярна плоскости (SAB)! Тогда у нас возникли ещё прямоугольные треугольники, в которых также можно посчитать отрезки ;)
Обозначим центр основания за
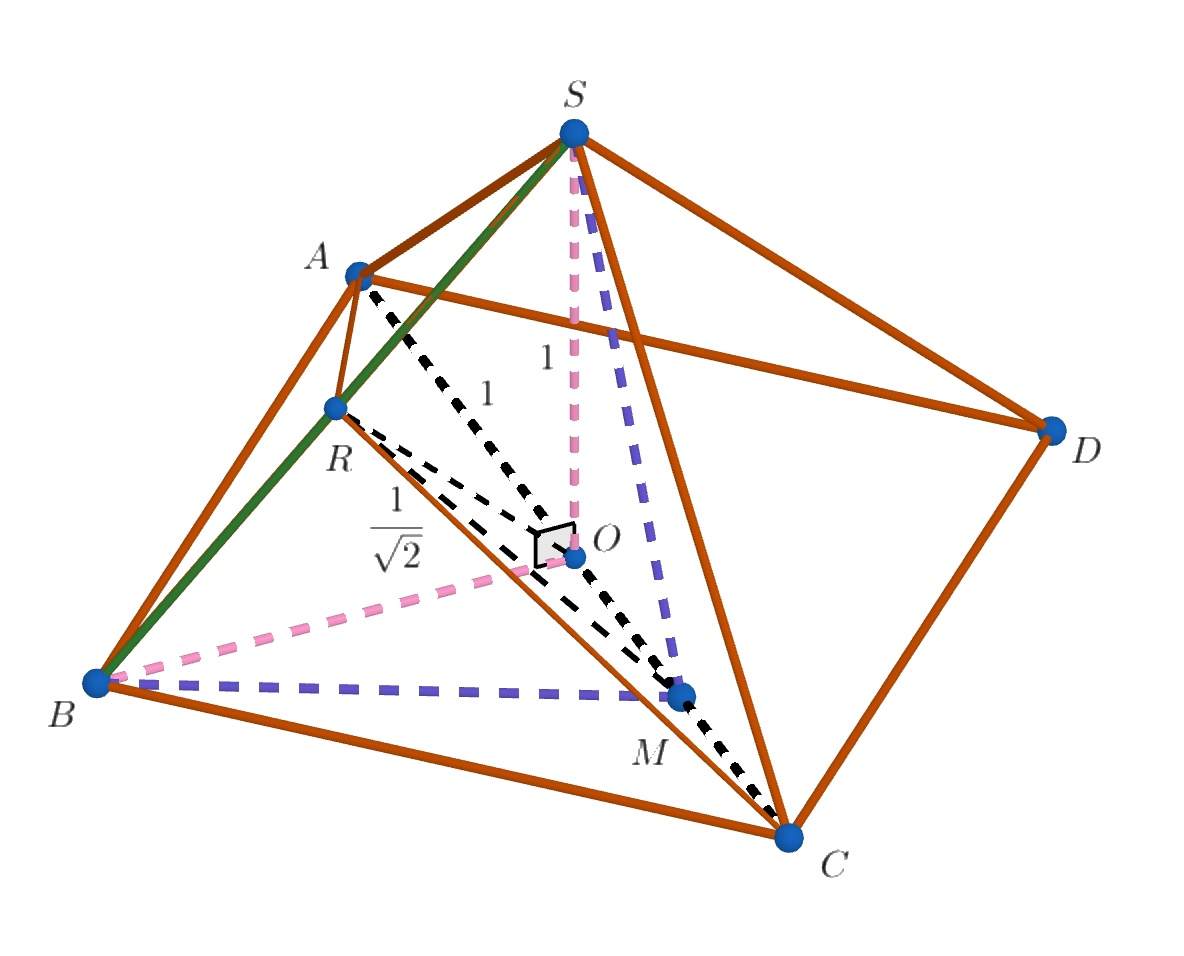
Тогда и
откуда
Это означает, что серединный перпендикуляр к отрезку
(это плоскость,
обозначим её за
) параллелен
С другой стороны, из
следует, что точка
лежит в
Тогда и вся прямая
должна содержаться в
Отсюда получаем
Середину обозначим за
. Заметим, что
лежит сразу в двух плоскостях, перпендикулярных
:
и
Это
означает, что
и сам перпендикулярен плоскости
а также отрезку
Примем длину за
Тогда
является медианой в прямоугольном равнобедренном треугольнике
; так как катеты этого треугольника равны по
имеем
.
Наконец, рассмотрим сечение тетраэдра плоскостью
Треугольник прямоугольный, причём
в нём — высота к гипотенузе. Имеем
, то есть
,
откуда
. Получаем
и
.
Замечание.
Утверждение о том, что боковое ребро пирамиды перпендикулярно скрещивающейся с ним диагонали, считается очевидным; за отсутствие его доказательства баллы не снижаются.
Ошибка.
Попробуйте повторить позже
Докажите, что существуют такие последовательности натуральных чисел и
что одновременно выполнены следующие
условия:
- последовательности и
являются неубывающими;
- последовательности и
неограниченно возрастают;
- последовательность ограничена.
Источники:
Подсказка 1
Попробуем строить последовательности а и b вокруг последовательности С. Пусть каждый k-тый член в ней равен 2 в степени (-k) — такая последовательность, конечно, ограничена. Как теперь собрать такие последовательности а и b, чтобы max(aₙ, bₙ)=cₙ?
Подсказка 2
Вспомним про раскраски! Разобьём натуральный ряд на цветные отрезки, и для каждого цвета одно число (аₙ или bₙ) равно 2^n, а второе число должно быть меньше него. Как бы это реализовать?
Подсказка 3
Для каждого числа "не на своём цвете" будем брать 2 и возводить в самое маленькое число на этом отрезке! То есть, если красный отрезок начинается с числа k, то (не умаляя общности) аₙ равен 2^n, а bₙ равен 2^k (для синих отрезков аналогично с точностью наоборот). Тогда мы действительно можем составить нашу последовательность c, а так же обе последовательности а и b будут неубывающими. Но как сделать так, чтобы и последовательности А и В были неограниченно возрастающими? Хорошо бы было, если бы на каждом красном отрезке сумма обратных значений b не была слишком маленькой...
Подсказка 4
Конечно! Пусть длина каждого отрезка, начинающегося на k, равна 2^k! Тогда сумма обратных на каждом отрезке равна единице, и последовательности будут не ограничены сверху!
Рассмотрим последовательность . Ясно, что все суммы
ограничены. Будем строить исходные последовательности и
так, чтобы
. Последовательно разобьём
натуральный ряд на отрезки подряд идущих чисел так, что если отрезок начинается с числа
, то его длина равна
. После этого
раскрасим все эти отрезки поочередно в красный и синий цвета.
Теперь зададим последовательность следующим образом:
- если - красное число, то положим
равным числу
;
- если - синее число, то положим
равным
, где
- первое число отрезка, содержащего
.
Последовательность зададим аналогично, но инвертируя цвета:
- если - синее число, то положим
равным числу
;
- если - красное число, то положим
равным
, где
- первое число отрезка, содержащего
.
Заметим, что для каждого синего отрезка сумма обратных значений последовательности на нём равна
поэтому
последовательность сумм
не ограничена сверху. Аналогично, для последовательности
сумма обратных значений на
каждом красном отрезке равна
поэтому последовательность сумм
не ограничена сверху.

