Тема Курчатов - задания по годам

Курчатов 2018

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела курчатов - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#30988

Вычислите значение выражения

(34+4)(74+ 4)(114+ 4)...(20154 +4)(20194+ 4) -(14+4)(54-+4)(94-+4)...(20134+-4)(20174+-4)-.

Источники: Курчатов-2018, 9.3 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Нам нужно провести какие-то преобразования с дробью, ибо пока она никак не сокращается. Подумаем, что бы мы могли преобразовать. Давайте попробуем выражение n⁴ + 4 разложить на множители. Тогда мы сможет посокращать получившиеся множители в числителе и знаменателе, и получить более красивую дробь.

Подсказка 2

Итак, значение n⁴+ 4 , воспользуемся тем, что
n⁴ + 4= (n² + 2)² − 4n². И попробуем преобразовать это выражение, а затем и наши скобки.

Показать ответ и решение

Посчитаем сначала значение $n4+ 4$ :

4 2 2 2 2 2 2 2 n + 4= (n + 2) − 4n = (n +2 − 2n)(n + 2+ 2n)=((n− 1) + 1)((n +1) + 1)

Подставим это вместо каждой такой скобки в дробь, получим:

(22-+1)(42+-1)(62+-1)...(20202+-1) 2 (02 +1)(22+ 1)(42+ 1)...(20182+ 1) = 2020 + 1.

Ответ:

$4080401$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#49160

Вершины правильного $100$ -угольника раскрашены случайным образом в два цвета: $50$ вершин — в белый цвет, $50$ — в черный. Докажите, что можно разбить все вершины на $25$ групп по $4$ вершины так, чтобы в каждой группе было по две вершины каждого цвета, и вершины каждой группы являлись вершинами некоторого прямоугольника.

Источники: Курчатов-2018, 11.2 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Давайте подумаем, а как красивым способом получить прямоугольники? И для чего нам условие правильности 100угольника, что с ним можно сделать?

Подсказка 2

Можно провести 50 диаметров этого 100угольника, тогда любые два диаметра являются диагоналями некоторого прямоугольника! Значит, нам нужно разбить их на 25 пар, в каждой из которых поровну черных и белых концов! Что для этого достаточно?

Подсказка 3

Чтобы полностью чёрных диаметров было столько же, сколько и полностью белых. Осталось лишь подумать, почему это так)

Показать доказательство

Проведём $50$ диаметров нашего $100$ -угольника. Нам требуется разбить их на пары так, чтобы в каждой паре было поровну чёрных и белых вершин. Для этого необходимо и достаточно, чтобы полностью чёрных диаметров было столько же, сколько и полностью белых. Действительно, если это не так, то один из таких диаметров останется без пары — ему не подойдут разноцветные диаметры. Если же это так, то мы бьём все одноцветные на пары с одинаковыми цветами, после чего остальных останется чётное количество (всего диаметров $50$ ) и их можно разбить как угодно.

Итак, почему же чёрных диаметров столько же, сколько и белых? Каждый разноцветный диаметр содержит одинаковое количество белого и чёрного цвета, потому на одноцветные приходится также равное количество этих двух цветов (изначально каждого по $50$ ). Но раз так, то количество чёрных и белых диаметров будет одинаковым, чтобы они содержали равное количество разных цветов, что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 3#73405

Натуральные числа $1,2,...,64$ записаны в клетках таблицы $8×8$ так, что для всех $k =1,2,3,...,63$ числа $k$ и $k+1$ находятся в соседних по стороне клетках. Каково максимальное значение возможной суммы чисел на главной диагонали?

Подсказки к задаче

Подсказка 1

Так-с, ну пример здесь приводить трудновато. Начнём с оценки. Возможно нам нужна раскраска... Действительно, соседние клетки отличаются на 1. Какая же раскраска будет полезна? Да, точно, в данном случае нам пригодится шахматная раскраска!

Подсказка 2

Давайте подумаем насколько большим может быть минимальное число на диагонали. В одной из сторон от диагонали лежит 1...Чуть чуть ещё поразмыслив, получаем оценку на число 26.

Подсказка 3

А как оценить остальные числа на диагонали? Они должны быть одной чётности, значит легко можно получить оценку на чётные числа от 52 до 64. Пример тоже придумать не так сложно!)

Показать ответ и решение

Оценка. Раскрасим клетки таблицы в шахматном порядке так, чтобы клетки на выбранной главной диагонали были белыми. Не умаляя общности, можно считать, что единица стоит не выше диагонали. Найдем максимальное значение наименьшего числа, попавшего на диагональ. Поскольку соседние числа стоят в клетках разного цвета, а белых клеток под диагональю находится всего $12,$ то одно из чисел от $1$ до $26$ обязательно попадает на диагональ. Остальные числа на диагонали гарантированно имеют одну четность, поэтому их сумма не превосходит суммы четных чисел от $52$ до $64.$ В итоге заключаем, что для суммы чисел на диагонали есть оценка сверху:

26 +52+ 54+56+ 58+ 60 +62+ 64= 432.

Пример подходящей расстановки:

$PIC$

Ответ:

$432$

Ошибка.
Попробуйте повторить позже

Задача 4#76411

В остроугольном треугольнике $ABC$ через вершину $A$ проведена прямая $ℓ$ , перпендикулярная медиане, выходящей из вершины $A$ . Продолжения высот $BD$ и $CE$ треугольника пересекают прямую $ℓ$ в точках $M$ и $N$ . Докажите, что $AM =AN$ .

Источники: Курчатов - 2018, 9.4(см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Сразу определим векторы, соответствующие сторонам треугольника и медиане. Как записать перпендикулярность «на языке векторов»?

Подсказка 2

Перпендикулярность векторов записываем как нулевое скалярное произведение! Теперь у нас есть 3 уравнения (скалярных произведения), попробуем их преобразовать и сделать выводы!

Подсказка 3

Нужное скалярное произведение есть 31/65 от суммы квадратов длин векторов AO и BO. А как учесть угол?)

Показать доказательство

Первое решение. Пусть $−A→B = ⃗b,−A→C = ⃗c,−A−M→ =⃗u$ и $−A−N→ =⃗v.$ Прямая $MN$ перпендикулярна медиане, следовательно,

⃗ ⃗u ⋅(b+ ⃗c)=0.

С другой стороны, $BM ⊥ AC$ и $CN ⊥ AB$ , поэтому

⃗ ⃗ (b− ⃗u)⋅⃗c= (⃗v− ⃗c)⋅b= 0.

Складывая три полученных равенства, выводим

(⃗u+ ⃗v)⃗b= 0

что возможно только если вектор $⃗u+ ⃗v$ нулевой, поскольку прямая $MN$ не перпендикулярна стороне $AB$ . Это обеспечивает равенство $AM =AN$ .

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Обозначим середину отрезка $BC$ за $T$ . Отразим точки $C$ и $N$ относительно $A$ , то есть построим точки $C′$ и $N ′$ такие, что $A$ является серединой отрезков $CC ′$ и $NN ′.$

$PIC$

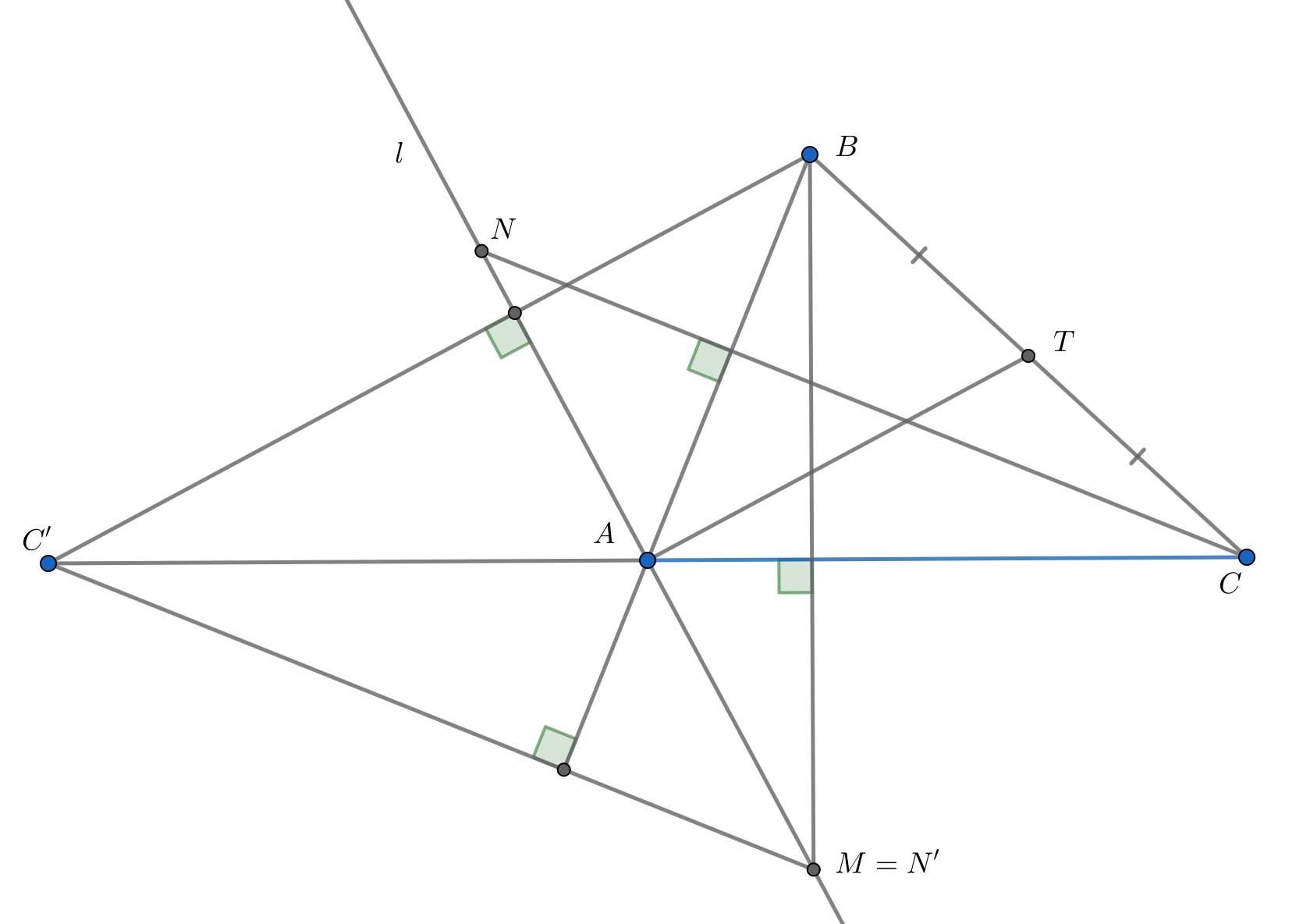
Ясно, что $C ′N′∥CN$ , что означает $C′N ′ ⊥BA$ . С другой стороны, $BM ⊥ C′A$ , так как $C′A$ и $CA$ - это одна и та же прямая. Наконец, отметим, что $ℓ⊥ C′B$ : это следует из того, что $ℓ$ перпендикулярна $AT$ , а $AT$ - средняя линия в треугольнике $CBA ′$ , то есть $AT ∥BC ′$ .

Осталось воспользоваться тем, что высоты $ℓ,BM$ и $C′N ′$ треугольника $ABC ′$ пересекаются в одной точке. Это означает, что $N′$ совпадает с $M$ , то есть $AM = AN ′ =AN$ .

Ошибка.
Попробуйте повторить позже

Задача 5#83238

Последовательность различных клеток $a ,a ,...,a 1 2 k$ клетчатого квадрата $n× n$ называется циклом, если, во-первых, $k ≥4$ , и, во-вторых, клетки $aj$ и $aj+1$ являются соседними по стороне при всех $j =1,2,...,k$ (считаем при этом, что $ak+1 = a1$ ). Множество $X$ клеток квадрата назовём разделяющим, если в любом цикле есть хотя бы одна клетка из множества $X$ . Найдите наименьшее вещественное число $C$ такое, что для любого натурального числа $n≥ 2$ в квадрате $n×n$ существует разделяющее множество из не более чем $2 C⋅n$ клеток.

Источники: Лига победителей - 2017, старшая лига (10 класс) и в том же условии Курчатов - 2018, задача 11.5

Подсказки к задаче

Подсказка 1

Кажется, все мы знаем раскраску, которая точно подойдёт под условие задачи. Точно! Давайте раскрасим квадрат в подобие шахматной раскраски с 3мя цветами. Очевидно, что условие задачи выполняется и мы получили пример на C = 1/3.

Подсказка 2

Как же доказать, что С не может быть меньше? С помощью графа! Давайте сделаем граф, вершинам которого соответствует стороны квадрата, а рёбрами соединим все соседние друг с другом клетки.

Подсказка 3

Теперь нужно удалить некоторые вершины так, чтобы в получившемся графе не было циклов. Если в графе нет циклов, то он является объединением деревьев, а максимальное количество рёбер в дереве очевидно ограничено сверху. Подобными рассуждениями можно выйти на нревенство, которое поможет строго оценить C.

Показать ответ и решение

Для построения примера разделяющего множества, в котором не более чем $n2∕3$ клеток, раскрасим все клетки в три цвета по диагоналям: первую диагональ - в первый цвет, вторую - во второй, третью - в третий, четвертую - опять в первый, и так далее.

$PIC$

Любой цикл из клеток, как легко видеть, пересекает как минимум три соседних диагонали и, следовательно, содержит клетки всех трех цветов. Клеток одного из цветов будет не более $n2∕3$ , и этот цвет можно использовать в качестве разделяющего множества.

Оценка. Покажем, что никакое $C < 1∕3$ не подходит.

Для этого построим граф, вершинами которого являются клетки. Две клетки соединим ребром, если они являются соседними. Получим граф, в котором $n2$ вершин и $2n(n − 1)$ ребер, при этом циклы задачи находятся во взаимно однозначном соответствии с циклами в графе. Требуется удалить несколько вершин так, чтобы в оставшемся графе не было циклов.

Предположим, мы удалили $k <C ⋅n2$ вершин. Если в оставшемся графе нет циклов, то этот граф является объединением деревьев и в нем не более чем $n2− k− 1$ ребро. При этом из каждой удаленной вершины выходило не более 4 ребер, и всего было удалено было не более $4k$ ребер. Таким образом, имеем неравенство

2 2n(n− 1)− 4k≤ n − k− 1,

откуда

(n − 1)2∕3 ≤k <C ⋅n2,

что невозможно при $C < 1∕3$ и достаточно большом $n$ .

Ответ:

$1 3$

Ошибка.
Попробуйте повторить позже

Задача 6#90887

Тетраэдр $ABCD$ с остроугольными гранями вписан в сферу с центром $O.$ Прямая, проходящая через точку $O$ перпендикулярно плоскости $ABC$ , пересекает сферу в точке $E$ такой, что $D$ и $E$ лежат по разные стороны относительно плоскости $ABC.$ Прямая $DE$ пересекает плоскость $ABC$ в точке $F$ , лежащей внутри треугольника $ABC.$ Оказалось, что $∠ADE = ∠BDE, AF ⁄= BF$ и $∘ ∠AF B = 80$ . Найдите величину $∠ACB.$

Подсказки к задаче

Подсказка 1

Нам бы очень хотелось, чтобы треугольники △ADE и △BDE оказались равны... Красиво ведь: равные углы, общая сторона, но условие о паре не равных отрезков рушит нам всё! Если они не равные, то что интересного можно заметить про эту пару?

Подсказка 2

В геометрических задачах часто бывает полезно посмотреть на каждое данное условие: зачем оно здесь, что можно из него вытащить? Из этих соображений было бы полезно посмотреть на точку Е — она может дать нам много равных отрезочков!

Подсказка 3

Итак, у вышеупомянутой пары треугольников есть две пары соответственно равных стороны и равные углы, но углы эти не между соответственно равными сторонами. Призовём на помощь теорему синусов, чтобы установить соотношение углов в этих треугольниках.

Подсказка 4

Всё равно нам пока не видно как выразить искомый угол... Красивую гипотезу о том, что F может быть центром окружности мы отмели ещё на условии о неравенстве отрезков, а делать что-то всё равно нужно. Попробуем провести доп построение, чтобы получить ещё один вписанный угол, опирающийся на дугу AB: попробуйте продлить AF до пересечения со сферой.

Подсказка 5

Самое время использовать свойства вписанного четырёхугольника и ту самую связь углов, которую мы получили ранее. Двух пар соответственно равных углов и общей стороны треугольников вполне достаточно, чтобы сделать выводы о равенстве!

Подсказка 6

Видим красоту: в плоскости (АВС) внезапно появился равнобедренный треугольник с искомым углом при основании и известным внешним углом. Осталось лишь немного счёта и задача решена :)

Показать ответ и решение

$PIC$

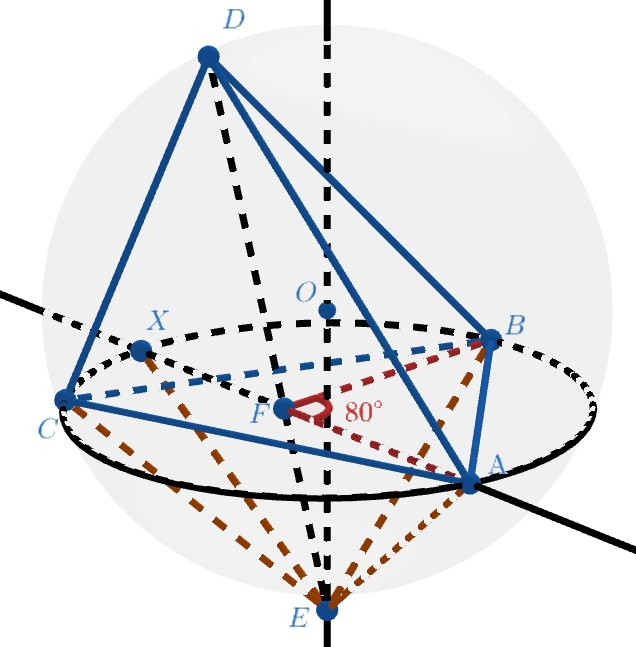
Первое решение.

Заметим, что точка $E$ равноудалена от точек $A,B,C$ , так ее проекция на плоскость $ABC$ совпадает с проекций точки $O$ на эту плоскость и является центром описанной окружности треугольника $ABC$ .

Рассмотрим треугольники $ADE$ и $BDE.$ Они имеют пару равных сторон $AE$ и $BE$ , общую сторону $DE$ и равные углы $ADE$ и $BDE.$ Из теоремы синусов следует, что эти треугольники либо равны, либо углы $DAE$ и $DBE$ дополняют друг друга до $180∘.$ Первая ситуация невозможна, так как в случае равенства треугольников $ADE$ и $BDE$ точки $A$ и $B$ равноудалены относительно любой точки на стороне $DE$ , но по условию $AF ⁄=BF.$ Значит, $∠DAE + ∠DBE = 180∘.$

Рассмотрим точку $X$ пересечения луча $AF$ со сферой $Ω$ , описанной около тетраэдра $ABCD.$ Заметим, что луч $AF$ лежит в плоскостях $ABC$ и $AED$ , а значит точка $X$ лежит на описанных окружностях треугольников $ABC$ и $AED.$ Точка $E$ равноудалена относительно всех точек описанной окружности треугольника $ABC;$ в частности, $AE = XE.$ Из вписанности четырехугольника $AEXD$ следует, что $∠DAE + ∠DXE = 180∘.$ Раз $AE = XE$ , то $E$ - середина дуги $AX$ описанной окружности треугольника $ADE$ , и значит $∠ADE =∠XDE$ .

Используя выведенные ранее равенства углов, заключаем, что треугольники $DBE$ и $DXE$ равны по второму признаку:

∠DBE = 180∘ − ∠DAE =∠DXE, ∠XDE = ∠ADE = ∠BDE,

сторона $DE$ – общая. Раз треугольники $DBE$ и $DXE$ равны, то вершины $B$ и $X$ равноудалены относительно любой точки на стороне $DE;$ в частности, $BF = FX$ .

Осталось посчитать углы в плоскости $ABC.$ Последовательно используя вписанность четырехугольника $ABXC$ , равнобедренность треугольника $BFX$ и теорему о внешнем угле для треугольника $BF X$ , пишем

∠ACB =∠AXB = 1⋅(∠FXB + ∠FBX )= 1⋅∠AF B = 40∘ 2 2

________________________________________________________________________________________

Второе решение.

Пусть луч $AF$ пересекает сферу $Ω$ , описанную около тетраэдра $ABCD$ , в точке $X$ . По построению точки $E$ верно соотношение $EX = EA$ , которое влечет за собой равенство $∠ADE = ∠EAF$ . Аналогичными рассуждениями получаем, что $∠BDE = ∠EBF$ , и, следовательно, $∠EAF = ∠EBF$ .

Обозначим точку пересечения прямой $OE$ с плоскостью $ABC$ , являющуюся центром описанной окружности треугольника $ABC$ , через $O1$ . Тогда $∠O1AE = ∠O1BE$ .

Рассмотрим трехгранные углы $AO1EF$ и $BO1EF$ . В них совпадают плоские углы $EAF$ и $EBF$ , плоские углы $O1AE$ и $O1BE$ и двугранные углы при ребрах $AO1$ и $BO1$ прямые. Следовательно, соответствующие трехгранные углы равны. А значит равны и плоские углы $∠FAO1 =∠F BO1$ . Отметим, что это равенство можно вывести и из теоремы косинусов для трехгранных углов. Указанное равенство возможно в двух случаях: либо точка $F$ лежит на серединном перпендикуляре к $AB$ (точки $A$ и $B$ симметричны относительно $FO1$ ), либо точка $F$ лежит на описанной окружности треугольника $ABO 1$ . Первый случай запрещен условием $AF ⁄= BF$ , значит, имеет место второй. Тогда $∠AOB = ∠AFB = 80∘$ и является центральным для угла $ACB$ в описанной окружности треугольника $ACB$ . В результате заключаем, что $∘ ∠ACB =40$ .

Ответ:

$40∘$