Росатом 2020
Ошибка.
Попробуйте повторить позже
Арифметическая прогрессия 
с ненулевой разностью такова, что последовательность 
также арифметическая
прогрессия с ненулевой разностью. Найти возможные значения первого члена и разности прогрессии 
если для всех 
справедливо
равенство 
Источники:
Подсказка 1
Какие выводы можно сделать из уравнения 2cos²(aₙ) = cos(a_{n+1}). Попробуйте выразить cos(aₙ).
Подсказка 2
При всех n cos(a_{n+1}) ≥ 0 и |cos(aₙ)| = √( cos(a_{n+1}) / 2 ) ≤ 1 / √2. Что тогда можно сказать об aₙ?
Подсказка 3
Все значения aₙ попадают на участок [π/4;π/2]. Попробуйте подумать о разности арифметической прогрессии - d.
Подсказка 4
Что, если d будет больше ближайшего к aₙ числа, кратного 2π?
Подсказка 5
Тогда некоторый член последовательности выйдет за пределы [π/4;π/2]. Проведите аналогичные рассуждения в меньшую сторону.
Подсказка 6
Получим, что d кратно 2π, или d = 2πk, k ∈ ℤ. Как мы можем это использовать?
Подсказка 7
Выразите cos(aₙ) при помощи a₁ и d.
Подсказка 8
Получится, что cos(aₙ) = cos(a₁). Подставьте это в уравнение из условия.
Подсказка 9
Мы получим несколько решений относительно a₁, выразите через них aₙ и bₙ.
Из уравнения
следует, что при всех 
На тригонометрическом круге все значения 
попадают на участок ![[π π]
4;2 .](/api/latex-service/v1/GetSession/260298/index-354afaef73fbd9c68828efcb338ac1dc.svg)
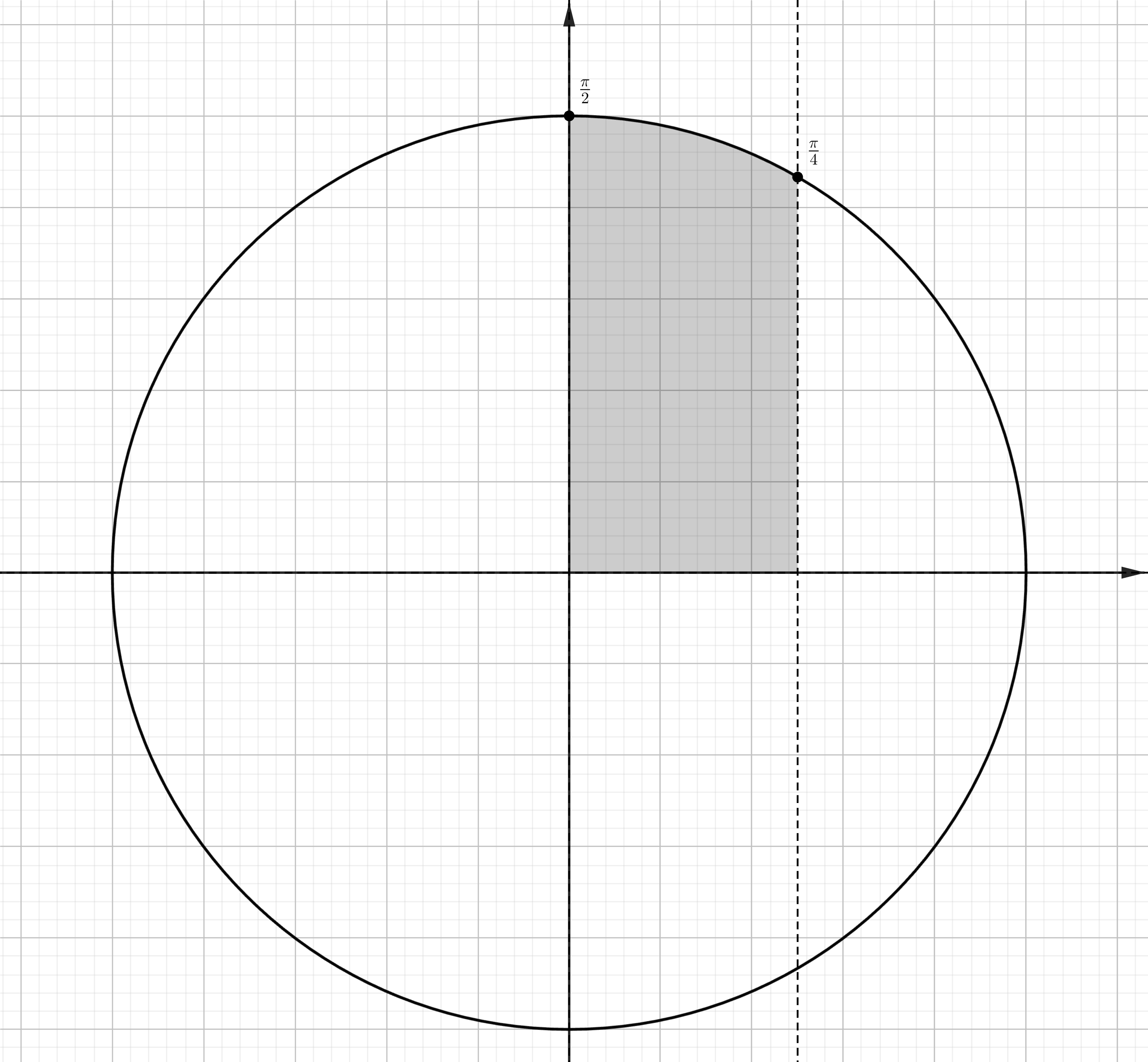
является арифметической прогрессией, докажем, что ее разность 
должна быть кратна длине окружности
Если бы величина 
была больше ближайшего к 
числа, кратного 
то один из следующих членов последовательности,
располагаясь на единичной окружности против часовой стрелки от 
и смещаясь от него на постоянное значение вдоль дуги, выйдет за
участок ![[ ]
π4;π2 .](/api/latex-service/v1/GetSession/260298/index-03093646052c75b753e8fc62492005e3.svg)
Аналогично, если величина 
меньше ближайшего к 
числа, кратного 
то один из следующих членов прогрессии, располагаясь
по часовой стрелке от 
и смещаясь от него на постоянное значение вдоль дуги, выйдет за участок ![[π4;π2].](/api/latex-service/v1/GetSession/260298/index-ba4ae54c9aa6a20d9420212cc4897b48.svg)
Тогда получаем, что
По условию, 
следовательно, 
Получаем, что при всех 
Определим первый член прогрессии
Тогда из первого решения получаем
Из двух оставшихся
1) 
2) 
3) 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
