Росатом 2019
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
совершенно случайно взяты точки
и
. Найти вероятность того, что площадь
треугольника
окажется не меньше трети площади треугольника
.
Подсказка 1
Хм, как же решать такую задачу...Нам поможет графический подход. Давайте нарисуем квадрат 1:1 и будем наугад выбирать точку, координаты которой соответствуют отношению, в котором точки из условия делят сторону треугольника.
Подсказка 2
Так, искомая вероятность тогда равна площади под графиком. Вот теперь начинаются фокусы. Не испугаемся и возьмём неопределённый интеграл!
Обозначим . Тогда имеем условие
, где
равномерно распределены на отрезке
.
Представим это в виде квадрата
— выбор
аналогичен выбору случайной точки из квадрата:
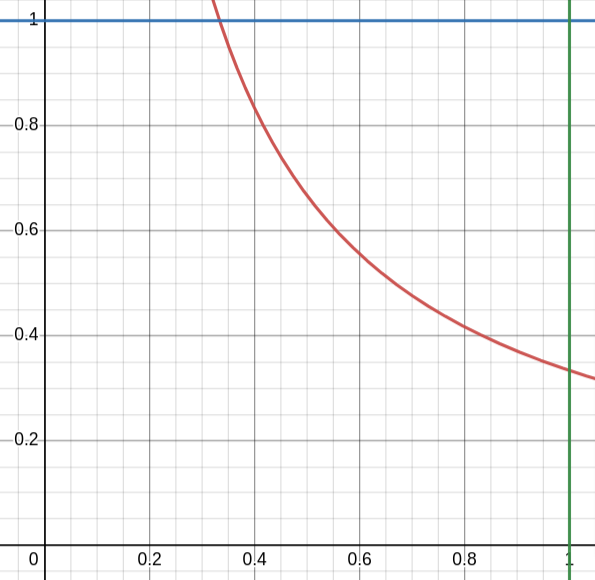
Нас интересует площадь над гиперболой внутри этого квадрата.
Гипербола пересекается с прямой при
, поэтому для искомой площади нам нужно из площади прямоугольника
вычесть площадь под гиперболой, которая равна
Итак, получаем
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
совершенно случайно взяты точки
и
. Найти вероятность того, что площадь
треугольника
окажется не больше половины площади треугольника
.
Источники:
Подсказка 1
Хм, как же решать такую задачу... Нам поможет графический подход. Давайте нарисуем квадрат 1:1 и будем наугад выбирать точку, координаты которой соответствуют отношению, в котором точки из условия делят сторону треугольника.
Подсказка 2
Так, искомая вероятность тогда равна площади под графиком. Вот теперь начинаются фокусы. Не испугаемся и возьмём неопределённый интеграл!
Обозначим . Тогда
, где
равномерно распределены на отрезке
. Представим это в
виде квадрата
— выбор
аналогичен выбору случайной точки из квадрата.
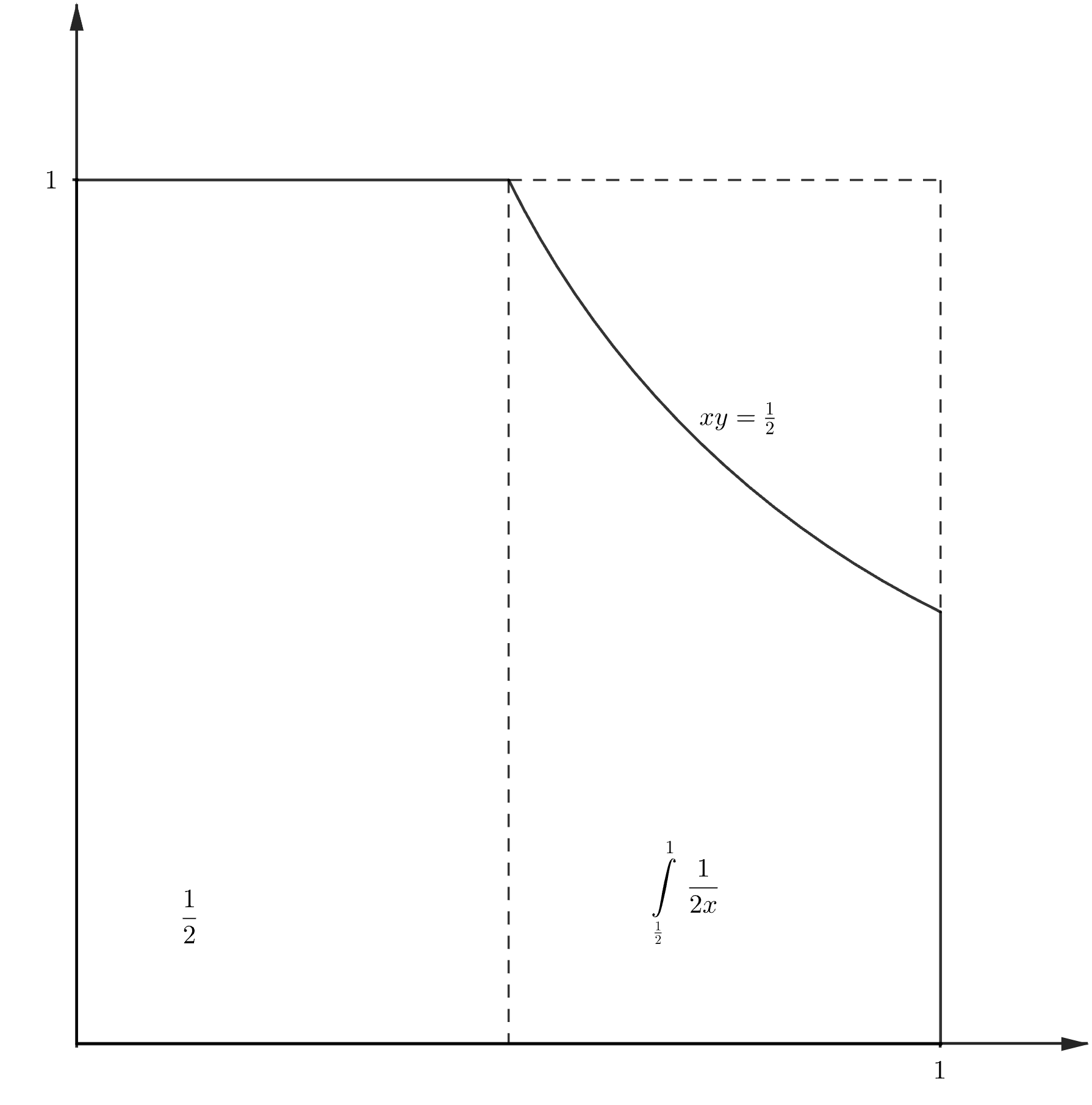
Нас интересует площадь под гиперболой внутри этого квадрата, которая равна
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
расположены точки
и
так, что
. Точка
– середина отрезка
, точка
– середина стороны
Угол при вершине
треугольника
равен
Найти длину отрезка
Источники:
Подсказка 1
Вспомните, как векторно выразить среднюю линию четырёхугольника
Подсказка 2
Затем вспомните, что длина это корень из скалярного квадрата
Первое решение.
Давайте вспомним, что отрезок между серединками каких-то сторон может быть удобно посчитать через векторы:
Тем более нам дан угол между векторами и
— он равен углу между векторами
и
(ведь
сонаправлен
, а
сонаправлен
) то есть
градусам. Осталось вспомнить, что длина связана со скалярным
квадратом:
Раскрываем квадрат суммы:
Отсюда
Второе решение.
![]()
Давайте заметим, что если сдвинуть точку и
по стороне
на вектор
, то условие останется выполненным, а точки
и
сдвинуться на вектор
. Значит длина
не измениться. Аналогично, можно сдвинуть точки
и
вдоль
так, чтобы условие и
длина
сохранилась. Сдвинем
и
в точку
и получим.
![]()
Тогда ,
и
. Значит, перед нами равносторонний треугольник и
медиана в нем. Значит, ее
длина равна
Ошибка.
Попробуйте повторить позже
Ученикам на входе в школу разрешалось брать из коробки любое количество карандашей. Позже выяснилось, что не менее
карандашей, полученных любой группой из десяти человек, оказывались у одного ученика из этой группы. Докажите, что в школе есть
ученик, забравший более
карандашей, взятых всеми школьниками из коробки.
Источники:
Подсказка 1
Нам нужно доказать, что существует ученик, который взял достаточно много карандашей. Также есть условие про то, что в любой группе из 10 человек есть человек, который взял хотя бы 60 процентов карандашей из их группы. Это наталкивает на мысль упорядочить учеников по убыванию кол-ва взятых ими карандашей и доказывать что-то про ученика, который взял больше всех!
Подсказка 2
Давайте попробуем записать условие про группу из 10 человек, которые идут подряд по убыванию после нашего упорядочивания) Выйдет что-то вида x_k/(x_k + x_{k+1}+..+x_{k+9}) >= 0,6. Во что это можно преобразовать, чтобы получить оценку x_k через другой один x?
Подсказка 3
Например, можно получить что x_k >= 27/2 * x_{k+9}! Мы понимаем, что мы умеем оценивать x_1 через первые 10 иксов. А можем ли мы оценить теперь сумму вообще всех иксов через сумму первых десяти иксов?
Подсказка 4
Можем! С помощью нашего полученного неравенства) Остаётся только использовать обе эти оценки, чтобы получить оценку x_1 через сумму всех иксов, и станет понятно, что задача решилась!
Пусть ученики школы упорядочены по убыванию числа взятых ими карандашей: ученик под номером взял из коробки
карандашей
и
По условию для любого выполняется неравенство. Преобразуем его
То есть для любого
Тогда для любого
По условию
Суммируя прогрессию, получим неравенство.
Если в школе учеников, то
Итого, ученик под номером забрал более
карандашей.
Ошибка.
Попробуйте повторить позже
В квадрате со стороной
расположена точка
отстоящая от сторон
и
на расстояние
Через точку
совершенно
случайно проводится прямая
разделяющая квадрат на две части. Найти вероятность того, что площадь одной из частей не превосходит
Подсказка 1
Что мы можем сказать об отсекаемой части? Какой у нее минимум или максимум площади? Какой случай для нашей прямой мы можем зафиксировать и отталкиваться от него?
Подсказка 2
Пусть М и N - точки пересечения нашей прямой со сторонами квадрата! Тогда наименьшая площадь отсекаемого квадрата появляется тогда, когда MD = MN. Какая она? Если точки пересечения будут другие(Х и Y), как изменится наша площадь квадрата? Выражать удобнее через отрезки, полученные с помощью точек на сторонах квадрата (например, проекций точки О на AD и DC). Поворачивая нашу прямую вокруг точки О, мы меняем угол между XY и NM. Какие углы нам подходят?
Подсказка 3
Пусть Н и Т это проекции О на DC и AD. Мы понимаем, что прямая из подсказки 2 нам подходит. Выразив площадь DYX через отрезок HX, понимаем, что мы можем крутить прямую до HX = 1(почему?). Осталось лишь осознать, какие значения угла HOX нам подходят и записать ответ!)
Случай прямая
пересекает стороны
квадрата
Пусть — проекции
на стороны
а в точках
прямая
пересекает эти стороны.
Если то
а прямая
делит квадрат на равные треугольники площадью по
Поэтому точки
различны, прямая
делит квадрат на треугольник и пятиугольник:
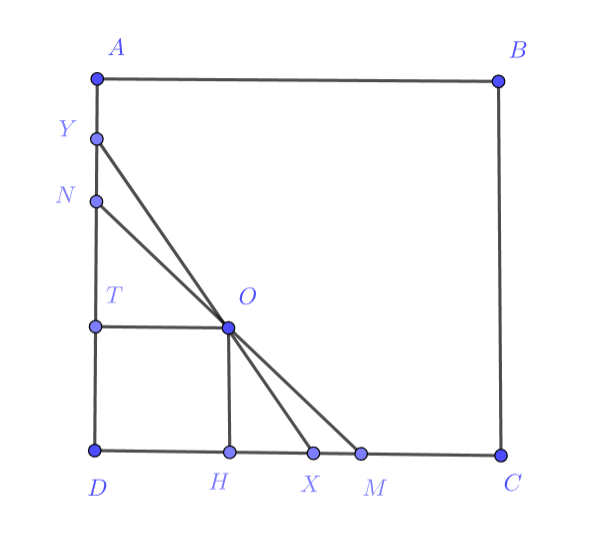
Обозначим С учётом
и подобия
получаем
Запишем условие на
площадь:
Мы выяснили, что нам подходят
и
как раз соответствуют случаям, когда
проходит через
и
и
соответственно.
Случай прямая
пересекается только с одной из сторон
то есть делит квадрат
на два четырёхугольника.
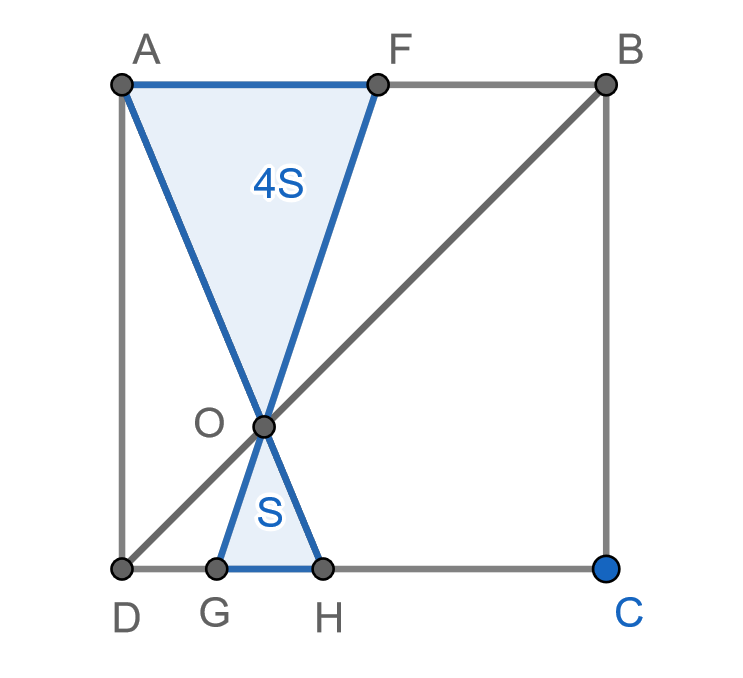
Покажем, что в таком случае площадь обоих частей Выше мы уже заметили, что в случае совпадения прямой
с прямой
или в случае совпадения с прямой
площадь меньшей из отсекаемых частей в точности равна
Предположим, что прямая пересекает стороны
Пусть она пересекает
в точке
в точке
Треугольники
подобны, при этом коэффициент подобия равен
поэтому
Заметим, что если мы перейдем от прямой к прямой
то площадь меньшей из частей увеличится на
Но так как площадь
то площадь
Случай, если пересекает стороны
разбирается аналогично (просто рассматривается прямая
вместо
).
В результате получаем ответ
Можно в числителе применить формулу разности арктангенсов
Ошибка.
Попробуйте повторить позже
Координаты вершин треугольника
являются решениями уравнения
Найти наименьшее возможное значение площади треугольника.
Подсказка 1
Какие знаки будут у выражений, записанных слева и справа?
Подсказка 2
Равенство достигается только тогда, когда обе части равны 0. Теперь надо решить простейшие тригонометрические уравнения.
Подсказка 3
Получим, что все вершины треугольника лежат на прямых двух семейств. Как теперь минимизировать площадь?
Подсказка 4
Попробуйте взять вершины треугольника на соседних прямых одного семейства.
Уравнение равносильно системе
Решения расположены в узлах «косой» решетки на плоскости образованной семейством прямых
Если две вершины, например, и
, искомого треугольника
наименьшей площади лежат на прямых семейства
, то
и
являются соседними вершинами решетки (в противном, его площадь может быть уменьшена) и
Вершина находится на соседней (параллельной) прямой из семейства
(иначе площадь может быть уменьшена). Поскольку
расстояние между соседними прямыми из семейства
одинаковое и равно
, площадь треугольника
равна
.
Если две вершины, например,
и
, находятся на прямой семейства
и являются соседними узлами решетки,
то
Вершина находится на соседней (параллельной) прямой семейства
Поскольку расстояние между соседними прямыми из
семейства
одинаковое и равное
, площадь треугольника равна
Ошибка.
Попробуйте повторить позже
Известно, что дробь сократимая для некоторых взаимно простых целых чисел
и
. Найти наибольшее простое число
,
на которое делится числитель и знаменатель дроби.
Подсказка 1
Если дробь A/B сократима на d, это значит, что и числитель A, и знаменатель B делятся на d без остатка. Запишите это по-умному.
Подсказка 2
Раз у нас d делит произведения, давайте рассмотрим возможные комбинации. Всего их четыре.
Подсказка 3
Посмотрите на условие: m и n — взаимно простые. Может ли у них быть общий простой делитель d? Подумайте, что это значит.
Подсказка 4
Вспоминаем важный приём из теории чисел: если d | a и d | b, то d делит и их линейную комбинацию (например, сумму). Примените это здесь.
Подсказка 5
Если d делит (m + 69n) и d делит m, то d делит их разность ((m + 69n) - m) = 69n. Мы знаем, что d простое. Может ли d делить n?
Подсказка 6
Разложите 69 на простые множители и сделайте вывод, каким может быть d. Разберите симметричный случай.
Подсказка 7
В последнем случае надо доказать, что d не может делить n, и тогда d будет делить (69² - 1). Разложите это число на простые множители.
Рассмотрим три случая
Если делится на
, и
делится на
, то и их разность делится на
, поэтому
делится на
, но
взаимно просто с
, следовательно и с
. Откуда
делится на
, значит,
.
Случай: делится на
, и
делится на
разбирается аналогично.
Если же и
делятся на
, то и число
делится на
.
Случай, когда делится на
был рассмотрен выше. Значит, можно считать, что
делится на
,
откуда в этом случае
.
Осталось привести пример на . Подходят
.



