Тема ОММО - задания по годам

ОММО 2018

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела оммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#32097

$n$ грибников ходили в лес и принесли суммарно $200$ грибов (возможно, некоторые из грибников не принесли домой ни одного гриба). Мальчик Петя, узнав об этом, заявил: «Какие-то двое из них обязательно принесли одинаковое количество грибов!» При каком наименьшем $n$ мальчик Петя наверняка окажется прав? Не забудьте обосновать свой ответ.

Источники: ОММО-2018, номер 2, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1!

1) Для начал было бы полезно примерно прикинуть оценку. В каком случае Петя не мог быть уверен, что у грибников есть двое с одинаковым количеством грибов?

Подсказка 2!

2) Верно, нужно допустить, что у всех было разное, и посчитать, сколько вообще можно взять грибников на 200 грибов! Только было бы здорово еще доказать, что при числах меньше нашей оценки он может быть не прав!

Показать ответ и решение

Для начала докажем, что при $n ≤20$ Петя может ошибиться. Предположим, что первые $n − 1$ грибников собрали соответственно $0,1,...,n − 2$ гриба, а $n$ -й - все остальные. Поскольку

0+ 1+ ...+ (n − 2)≤ 0+ 1+...+18= 171= 200− 29

то последний грибник собрал не менее $29$ грибов, т.е. больше, чем каждый из остальных. Итак, при $n ≤ 20$ существует пример, когда Петя мог быть не прав.

Покажем, что при $n= 21$ Петя всегда окажется прав. Предположим, что он не прав. Пусть грибники собрали $a <a < ...< a 0 1 20$ грибов. Несложно видеть, что $a ≥ i i$ , откуда получаем

200= a0+ a1+...+a20 ≥ 0+ 1+...+20= 210

противоречие.

Ответ:

$21$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#34206

Найдите все значения параметра $a$ , при каждом из которых уравнение

x2−2ax+a2 2 2 3 2 3 = ax − 2a x+ a +a − 4a+ 4

имеет ровно одно решение.

Источники: ОММО-2018, номер 8, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Очень хочется подсократить выражение, поэтому давайте сделаем замену t=x-a (повлияет ли это на количество решений?). Тогда что интересного можно заметить в обеих частях уравнения?

Подсказка 2

Конечно же симметрию! Если t - это решение, то -t тоже является решением! Отсюда получается и единственное значение t, которое должно быть решением уравнения! Осталось проанализировать, при каких именно значениях а, это решение будет единственным.

Подсказка 3

Получили а=1 и а=3. В первом случае попробуйте оценить 3^x снизу, чтобы выяснить количество решений для данного уравнения.

Подсказка 4

Во втором же случае удобно перебрать значения в нескольких точках, чтобы сделать вывод о количестве решений для данного уравнения!

Показать ответ и решение

Обозначим $x− a$ через $t$ . Заметим, что количество решений уравнения от такой замены не меняется. Тогда исходное уравнение приобретёт вид

t2 2 2 3 =at +a − 4a+ 4.

Заметим, что выражения в обеих частях не меняются при замене $t$ на $− t$ , поэтому нечётное число решений (в частности, ровно одно решение), это уравнение может иметь только если $t =0$ является его корнем:

0 2 3 = a⋅0+a − 4a+ 4,

т.е. $a2− 4a+ 3= 0$ , откуда $a= 3$ или $a= 1$ . Итак, кроме этих двух чисел, никакие другие значения параметра $a$ не могут удовлетворять условию.

Пусть $a = 1$ . Тогда уравнение примет вид $3t2 = t2+ 1$ . Заметим, что $3x > xln3+ 1$ при $x >0$ (что можно доказать, например, взяв производные обеих частей и учтя значение в нуле). Тогда при $t⁄= 0$ получаем $3t2 >$ $t2ln3 +1 >t2+ 1$ . Итак, при $a =1$ уравнение имеет единственное решение.

Пусть $a = 3$ . Тогда уравнение примет вид $3t2 = 3t2+ 1$ . Заметим, что $31 = 3,3⋅1+ 1= 4$ , но $322 = 81$ , $3⋅22+ 1= 13$ , т.е. при $t= 1$ левая часть меньше правой, а при $t= 2−$ наоборот. Следовательно, по теореме о промежуточном значении, уравнение имеет ещё хотя бы корень на интервале $(1,2)$ . Следовательно, $a= 3$ не удовлетворяет условию.

Ответ:

$1$

Ошибка.
Попробуйте повторить позже

Задача 3#36668

В трапецию $ABCD$ вписана окружность, касающаяся боковой стороны $AD$ в точке $K$ . Найдите площадь трапеции, если $AK = 16,DK =4$ и $CD = 6$ .

Источники: ОММО-2018, номер 4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Для начала подумаем, а какие данные нам нужны, чтобы найти площадь трапеции? Быть может, мы можем найти какие-то отрезки, если правильно воспользоваться информацией о касательных к вписанной окружности? Возможно, какая-то новая информация может показаться нам лишней, но условие кажется очень маленьким, поэтому любые новые знания нам нужны) Как же всё-таки воспользоваться длинами DK, CD и AK?

Подсказка 2

Отрезки касательных к одной окружности, проведенные из одной точки, равны! Это значит, например, что можно как-то обозначить все точки касаний окружности и сторон трапеции и найти почти все отрезки, на которые точки касания делят стороны) Теперь у нас есть одно из оснований, часть другого, нужна высота... Что же на нашем рисунке может намекать на перпендикулярность(связанное с окружностью)? Что для этого нужно отметить?

Подсказка 3

Вспоминаем, что некоторые радиусы вписанной окружности перпендикулярны сторонам. Тогда отметим у окружности центр I и опустим радиусы на каждую из сторон. Понятно, что радиусы на основания образуют высоту, т.е. теперь достаточно найти радиус. Для этого нам понадобится найти IK (перпендикуляр IK опущен на сторону, у которой мы знаем длины обоих отрезков). Какой факт о DI и AI можно использовать?

Подсказка 4

DI перпендикулярен AI! Тогда в прямоугольном треугольнике DIA мы можем найти высоту IK (из различных подобий), т.е. радиус. Аналогично можно поступить с прямоугольным треугольником CIB, тогда мы найдем еще один отрезок касательной, т.е. нам уже известна высота (2 радиуса) и оба основания, а, значит, и высота) Главное не ошибиться в счёте!

Показать ответ и решение

Первое решение.

Пусть точки касания с $CD,BC$ и $AB$ будут $N,M$ и $L$ соответственно. Из равенства отрезков касательных $DN = 4$ и $NC = CM =2$ , а также $AL= 16.$

$PIC$

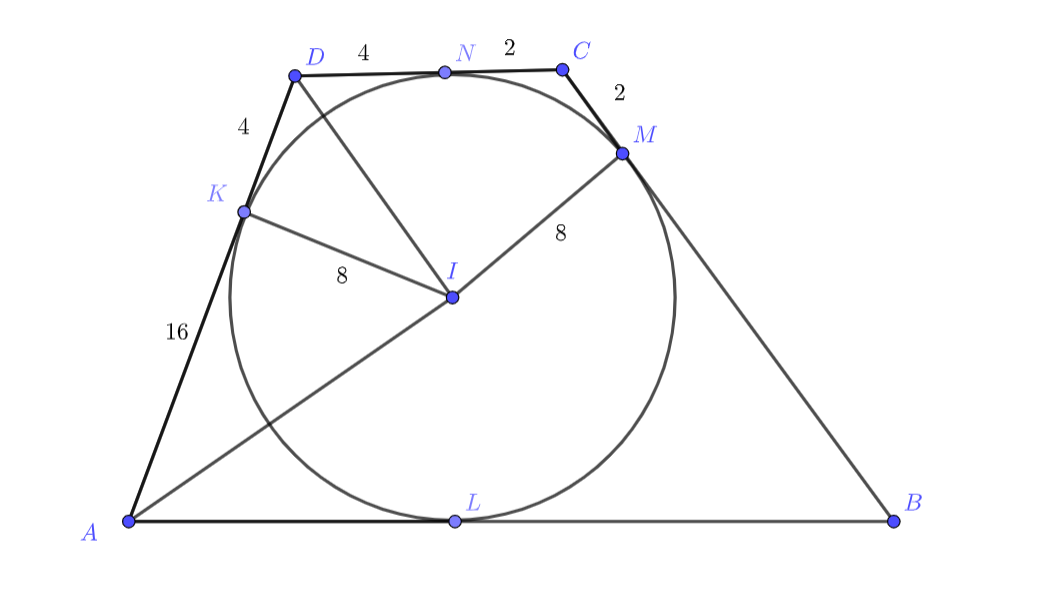
Как известно, $DI ⊥ AI$ , как биссектрисы углов трапеции, но тогда $KI$ — высота прямоугольного треугольника и равна $√ ---- 4⋅16 =8$ . Аналогично из прямоугольного $△BIC$ имеем $2 IM =CM ⋅BM =⇒ BM =32$ . Откуда легко посчитать, что $CD+AB- SABCD = 2 ⋅2NI =(16+ 32 +6)⋅8= 432$ .

Второе решение.

Пусть $N$ — точка касания окружности и стороны $DC.$ Так как $DK$ и $DN$ — отрезки касательных, то они равны. Значит, $DN = 4$ $⇒$ $NC = 2.$

Пусть $M$ — точка касания окружности и стороны $BC.$ Аналогично $NC = CM = 2.$

Пусть $L$ — точка касания окружности и стороны $AB.$ Проведем диаметр $NL$ и опустим высоту $DH$ на сторону $AB.$

$AK =AL = 16$ (как отрезки касательных), следовательно, $HL = DN = 4$ и $AH =AL − HL =12.$ Тогда по теореме Пифагора

∘--------- √ --- DH = AD2 − AH2 = 256= 16.

$PIC$

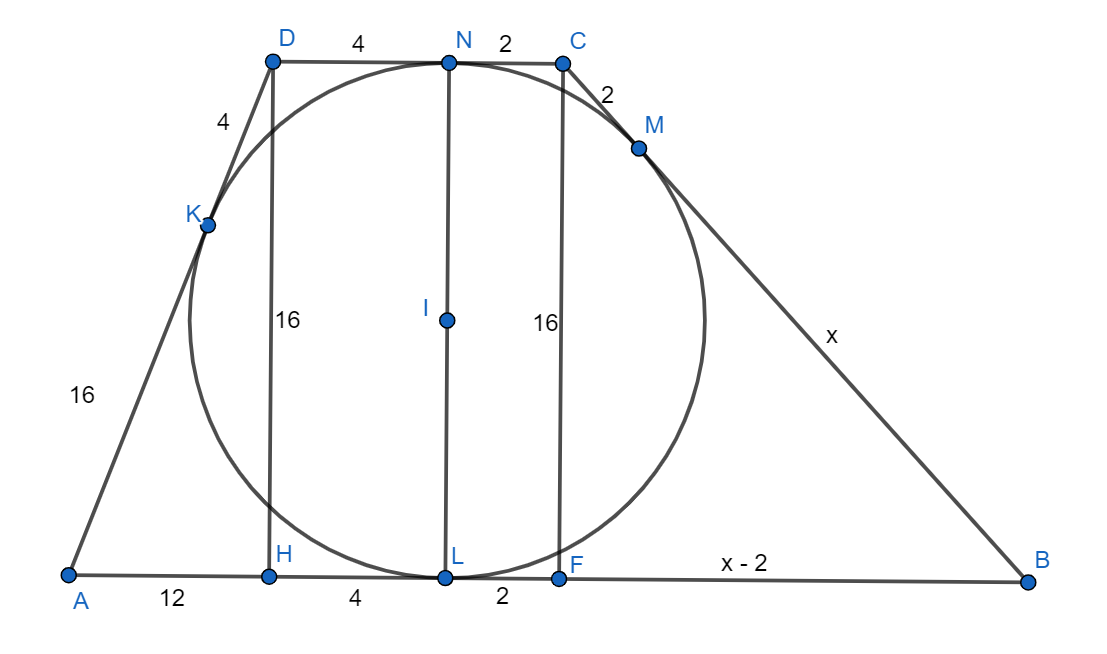
Опустим из точки $C$ перпендикуляр $CF$ на сторону $AB,$ он будет равен $16.$ Обозначим за $x$ отрезок $MB,$ тогда $FB = BL − LF = BM − 2= x− 2.$ По теореме Пифагора

2 2 2 (x+ 2) =16 + (x − 2)

2 8x =16

x= 32

Тогда

SABCD = DC-+2AB-⋅CF = 6+248⋅16= 432

Ответ:

$432$

Ошибка.
Попробуйте повторить позже

Задача 4#43271

Изобразите (с обоснованием) на координатной плоскости $Oxy$ множество решений неравенства

( 2 2 ) ( 2 2 ) y − arcsin (sinx) ⋅ y − arcsin(sin(x +π∕3))⋅

( 2 2 ) ⋅ y − arcsin(sin(x− π∕3)) <0.

Источники: ОММО-2018, номер 6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Мы работаем с арксинусами, в аргументах которых синусы -> прибавление к аргументу синуса 2π (или вычитание) ничего не изменит. Значит, нам достаточно работать только с отрезком длины 2π, возьмем, например, от -π/2 до 3π/2. Посмотрим на то, как именно раскрывается arcsin(sin(x)) на отрезках от -π/2 до π/2 и от π/2 до 3π/2.

Подсказка 2

На первом отрезке арксинус превратится в х², а на втором - в (π-х)². Тогда мы можем, грамотно применив разность квадратов, нарисовать области, которые нам подходят. Достаточно будет выбрать одну, и если она не будет подходить, то все соседние к ней подойдут, ведь при переходе через "ноль" будет меняться знак исходного выражения.

Подсказка 3

Важно отметить, что скобки отличаются собой только аргументами синуса, а это значит, что графики этих выражений будут идентичны и смещены друг от друга на расстояние π/3. Поэтому получится очень много квадратиков (так как изначально график любой изначальной скобки и составлял цепочку квадратов), и именно отсюда, после получения цепочек квадратиков нужно будет найти один подходящий, а затем дважды переходить через "ноль" и закрашивать нужную область.

Показать ответ и решение

Выражение слева не меняется при изменении $x$ на период $2π$ . Поэтому достаточно разобраться с графиком на отрезке длины $2π$ , например, $π 3π [−2; 2 ].$

Если $π π x∈ [− 2;2],$ то $2 2 arcsin (sinx)= x .$

Если $π 3π x∈ [2; 2 ],$ то $2 2 arcsin (sinx)= (π − x) .$

Рассмотрим в выражении из условия первую скобку, для второй и третьей построение будет аналогично, но со сдвигом на $π 3.$

Если $π π x∈ [− 2;2],$ то получаем неравенство $(y− x)(y+ x)<0.$

Если $π 3π x∈ [2;-2 ],$ то получаем неравенство $(y +π − x)(y +x− π)< 0.$

Теперь рассмотрим график ниже, отметим области под одной прямой и над другой:

$PIC$

$y2 − arcsin2(sinx)< 0$ в квадратах.

Для второй и третьей скобки будут те же квадраты, только сдвинутые на $π3$ и на $− π3$ по оси $x.$

Ответ:

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 5#49060

Вася хочет найти все целые числа $a$ такие, что выражение

3 5 10n − 3n +7an

делится на $15$ для всех целых $n$ . Какие остатки может давать число $a$ при делении на $15?$ Укажите все возможные ответы или докажите, что таких целых чисел $a$ нет.

Источники: ОММО-2018, номер 3, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

В задачах на делимость мы что делаем в первую очередь? Конечно, сравниваем выражение по модулю того числа, на которое оно должно делиться. Но 15 - число составное, с ним работать будет неудобно. Давайте перейдём для начала к сравнениям по модулю 3 и 5. Потом мы справимся найти остаток и по модулю 15. Нужно упростить наше выражение. Какую теорему можно вспомнить, чтобы это сделать?

Подсказка 2

Верно, есть малая теорема Ферма (она утверждает, что n^p сравнимо с n по модулю p), к тому же здесь удачно совпали степени. Попробуйте упростить теперь наше выражение по модулю 3 и 5. Как же можно в лоб найти остаток a?

Подсказка 3

Ага, мы нашли, что остаток при делении на 3 и 5 число -1. Теперь можно просто перебрать числа дающие остаток -1 по модулю 3, чтобы какой-то из них совпал по модулю 5. Китайская теорема об остатках утверждает, что такое число существует и единственное. Несложным перебором получается ответ, победа!

Показать ответ и решение

Первое решение.

По малой теореме Ферма $3 n ≡3 n$ и $5 n ≡5 n.$

Теперь взглянем на исходное выражение по модулю $3 :$

10n− 3n+7an ≡3 7n(a+ 1)≡3 0 =⇒ a≡3 −1

Теперь взглянем на исходное выражение по модулю $5 :$

10n3− 3n5+ 7an ≡5 − 3n +7an ≡5 7n+ 7an≡5 7n(a+ 1) =⇒ a ≡5 − 1

Итак, $a ≡3 − 1$ и $a ≡5 − 1$ . По Китайской теореме об остатках решение такой системы сравнений по модулю, равном произведению модулей, существует и единственно, легко находим, что это $a ≡15−1 ≡1514.$

Второе решение.

Подставим $n =1$ и получим, что если такое $a$ и существует, то $7+ 7a$ должно делится на $15,$ то есть $a$ должно давать остаток $14$ при делении на $15.$ Осталось проверить, что если $a ≡ 14 15$ , то указанное выражение делится на $15$ для любого натурального $n.$

Докажем это утверждение индукцией по $n$ (для $n= 0$ делимость очевидна, для отрицательных $n$ доказывается аналогично или сводится к случаю положительного $n$ заменой $n → −n)$ . Если $n= 1$ , утверждение уже проверено. Предположим теперь, что мы уже доказали, что $10n3− 3n5+ 7an$ делится на $15$ и докажем, что $10(n +1)3− 3(n+ 1)5+ 7a(n +1)$ также делится на $15.$ Посмотрим на разность этих двух выражений:

10((n+ 1)3− n3)− 3((n +1)5− n5)+ 7a((n+ 1)− n)= 10(3n2 +3n+ 1)− 3(5n4+ 10n3+10n2+ 5n +1)+ 7a.

После раскрытия скобок все слагаемые в правой части, кроме $10− 3+ 7a$ , делятся на $15,$ но $10− 3+7a$ делится на $15,$ поскольку $a ≡14 15$

Ответ:

$14$

Ошибка.
Попробуйте повторить позже

Задача 6#49308

Точки $A ,B ,C 1 1 1$ — точки пересечения продолжений высот остроугольного треугольника $ABC$ с описанной вокруг $ABC$ окружностью. Окружность, вписанная в треугольник $A1B1C1$ , касается одной из сторон $ABC$ , а один из углов треугольника $ABC$ равен $∘ 40$ . Найдите два других угла треугольника $ABC.$

Источники: ОММО-2018, номер 7, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

С помощью свойств ортоцентра докажите, что H - инцентр A_1 B_1 C_1

Подсказка 2

Нужно доказать, что треугольник H B C_{1} --- равносторонний.

Показать ответ и решение

Первое решение.

$PIC$

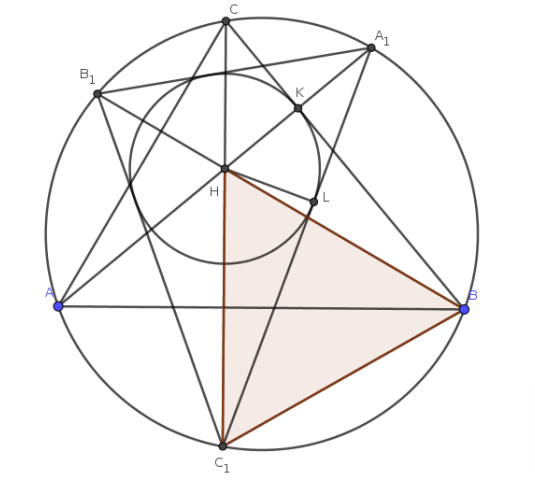
Не умаляя общности, пусть окружность $ω$ , вписанная в $A1B1C1$ , касается стороны $BC$ . Пусть $H$ - точка пересечения высот треугольника $ABC,K$ - точка касания $ω$ и $BC,L−$ точка касания $ω$ и $A1C1.$

Известно, что высоты $△ABC$ являются биссектрисами его ортотреугольника. При гомотетии с центром в точке $H$ и коэффициентом $2$ ортотреугольник переходит в $△A1B1C1,$ так что биссектрисы $△A1B1C1$ тоже пересекаются в точке $H.$

По свойству ортоцентра $H$ и $C1$ симметричны относительно прямой $AB$ , так что $HB = BC1.$ Кроме того, $∠HC1L = ∠HBK$ ( $∠HC1L = ∠CAA1 =90∘− ∠C =∠B1BC$ ), поэтому прямоугольные треугольники $HC1L$ и $HBK$ равны по катету ( $HL =HK$ ) и острому углу. Поэтому $HC1 =HB.$

В итоге получили $HC1 = HB = BC1.$ Тогда $∠BAC = ∠BC1C = 60∘$ , откуда с учётом условия и следует ответ.

Второе решение.

$PIC$

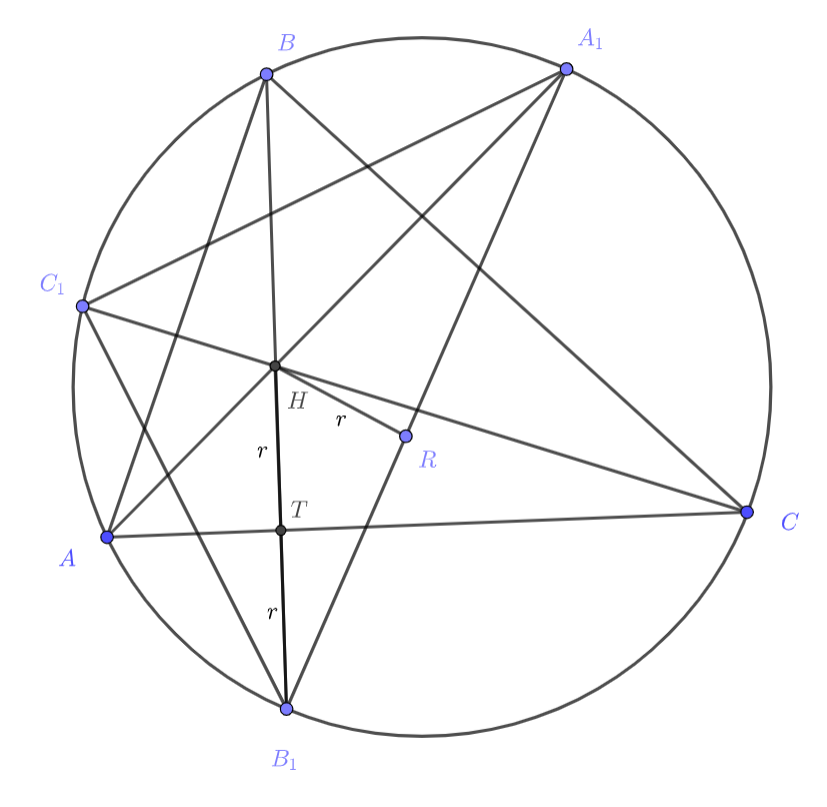
Пусть высоты $△ABC$ пересекаются в точке $H$ . Заметим, что

⌢ ⌢ ∠BB1C1 = ∠BCC1 =90∘− ∠ABC = ∠BAA1 =⇒ C1B = BA1

Отсюда следует, что $H$ лежит на биссектрисе угла $C1B1A1$ . Делая то же самое для остальных углов, имеем, что $H$ — центр вписанной окружности $△A1B1C1.$

Обозначим радиус этой окружности за $r$ и, не умаляя общности, $ρ(H,AC )=HT = r$ (касание из условия). Нетрудно видеть, что $BT$ является высотой треугольника $ABC$ . Поскольку мы уже знаем, что $⌢ ⌢ C1A= AB1$ ( $AA1$ — также биссектриса $△A1B1C1$ ), то $∠HCA = ∠ACB1 =⇒ HT = r= TB1$ (получили высоту и биссектрису $△HCB1$ ). Пусть также $HR ⊥ A1B1,R¯$ точка касания вписанной окружности. Тогда в прямоугольном $△HRB1$ катет равен половине гипотенузы и $30∘ = ∠HB1R = ∠HB1C1 =∠BCC1 =90∘− ∠ABC =⇒ ∠ABC =60∘$ . Поскольку мы знаем, что какой-то другой угол $△ABC$ равен $40∘$ , то третий будет $80∘.$

Ответ:

$60∘$ и $80∘$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#49483

Решите систему уравнений

(| x2 = (y− z)2− 3; { y2 = (z− x)2− 7; |( 2 2 z = (x− y) + 21.

Источники: ОММО-2018, номер 5, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

хм, пока не очень понятно, что можно сделать с этими уравнениями, а давайте попробуем перенести квадрат разности в другую часть и естственно применить разность квадратов.

Подсказка 2

заметим, что множители в наших трех итоговых уравнениях частично совпадают! // для удобства можно заменить их на a, b, c. тогда у вас есть ab, bc и ac, а надо найти каждое по отдельности, для этого помогло бы узнать abc, например!

Показать ответ и решение

Перенесём в каждом уравнении квадрат разности в левую части и применим формулу для разности квадратов:

(| (x− y +z)(x +y− z)= −3 { (y− z +x)(y +z− x)= −7 . |( (z− x +y)(z +x− y)= 21

Обозначим $X = −x+ y+ z,Y = x− y+ z,Z =x +y − z$ . Тогда

(| YZ =− 3 { ZX =− 7 |( XY = 21

Перемножая все получившиеся равенства, имеем $(XY Z)2 = 3⋅7⋅21$ , откуда $XY Z =21$ или $XYZ = −21.$

Разберём случай $XYZ = 21$ . В нём $X = (XYZ)∕(YZ)= −7,Y = −3,Z =1$ ; тогда $x= Y+2Z-=$ $− 1,y =− 3,z = −5.$

Второй случай разбирается аналогично и в нём $x= 1,y = 3,z = 5.$

Ответ:

$(−1,−3,− 5),(1,3,5)$

Ошибка.
Попробуйте повторить позже

Задача 8#92040

Докажите неравенство

log20151+-log20152+-...+-log20152016- log20152017 > 2016

Показать доказательство

Первое решение.

Так как

log20152017> log20152016> ...> log20151,

то

2016log20152017 >log20152016+ ...+ log20151

log 2017 > log20151+-log20152+-...+-log20152016- 2015 2016

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

После умножения обеих частей на 2016 и применения свойств логарифмов, получаем, что нам достаточно доказать неравенство

2016 log20152017 > log2015(1⋅2⋅...⋅2016)

Указанное неравенство следует из того, что $20172016 > 1⋅2⋅...⋅2016$ , а последнее получается перемножением 2016 неравенств $2017> 1,2017 >2,...,2017> 2016.$

Замечание. Можно получить и более сильную оценку, применим неравенство о средних:

2016√----------- 1+-...+2016 2017 1⋅2⋅...⋅2016≤ 2016 = 2 < 2017