Тема ИТМО - задания по годам

ИТМО 2018

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела итмо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#73684Максимум баллов за задание: 7

В некоторой стране $450$ городов и $6$ авиакомпаний. Каждые два города соединены рейсами одной из шести авиакомпаний. Можно ли утверждать, что найдется авиакомпания и больше $150$ городов, между любыми двумя из которых можно добраться рейсами этой авиакомпании (возможно, с пересадками)?

Источники: ИТМО 2018

Подсказки к задаче

Подсказка 1

Подобные задачи стоит начинать решать с попытки построения примера или антипримера.

Подсказка 2

Попробуйте разбить города на группы, связанные внутри рейсами одной авиакомпании.

Подсказка 3

Более того, можно сказать, что внутри любой группы города связаны рейсами первой авиакомпании. Теперь свяжите группы между собой так, чтобы получить противоречие утверждению из условия.

Показать ответ и решение

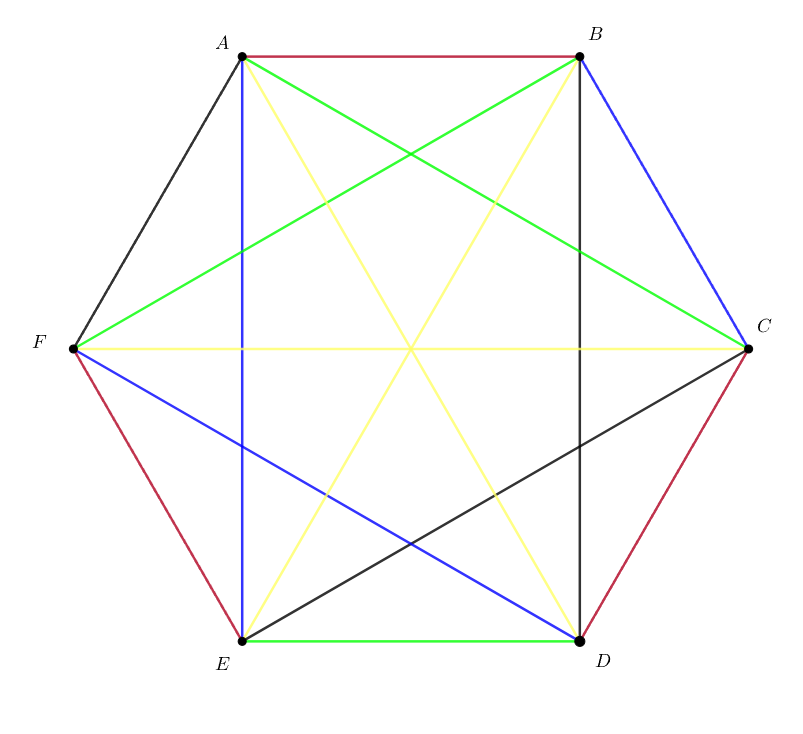
Построим контрпример. Разобьём города на $6$ групп по $75$ городов. Назовём эти группы $A,B,C,D,E,F.$

Внутри каждой группы соединим города рейсами компании номер $1.$

Компания номер $2$ будет соединять города группы $A$ с городами группы $B,C$ с $D,$ а $E$ с $F.$

Компания номер $3$ будет соединять города группы $A$ с городами группы $D,B$ с $E,$ а $C$ с $F.$

Компания номер $4$ будет соединять города группы $A$ с городами группы $C,B$ с $F,$ а $D$ с $E.$

Компания номер $5$ будет соединять города группы $A$ с городами группы $E,B$ с $C,$ а $D$ с $F.$

Компания номер $6$ будет соединять города группы $A$ с городами группы $F,B$ с $D,$ а $C$ с $E.$

Таким образом, рейсы компании номер $1$ связывают по $75$ городов, а рейсы остальных компаний ровно по $150.$

Это построение схематически изображено на рисунке. Разные компании обозначены разными цветами.

$PIC$

Ответ:

Нет