Тема ИТМО - задания по годам

ИТМО 2016

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела итмо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68312

Дан треугольник $ABC,$ точка $I$ — центр его вписанной окружности. На лучах $BI$ и $CI$ соответственно отмечены такие точки (отличные от $I$ ) $E$ и $F,$ что $AI = AE = AF.$ Докажите, что площади треугольников $BIF$ и $CIE$ равны.

Источники: ИТМО-2016, 10.7 (см. olymp.itmo.ru)

Подсказки к задаче

Подсказка 1

У нас есть интересное условие: AI = AE = AF... Никакое условие не напоминает?)

Подсказка 2

Лемма о трезубце! Давайте как раз обозначим за D середину дуги BC, и тогда DI = DB = DC. Попробуйте здесь найти подобия)

Подсказка 3

Да, можно доказать, что треугольники DIB и AIE подобны, также как DIC и AIF. Попробуйте записать эти условия подобий через отрезки, и сможете понять, почему площади требуемых треугольников равны)

Показать доказательство

$PIC$

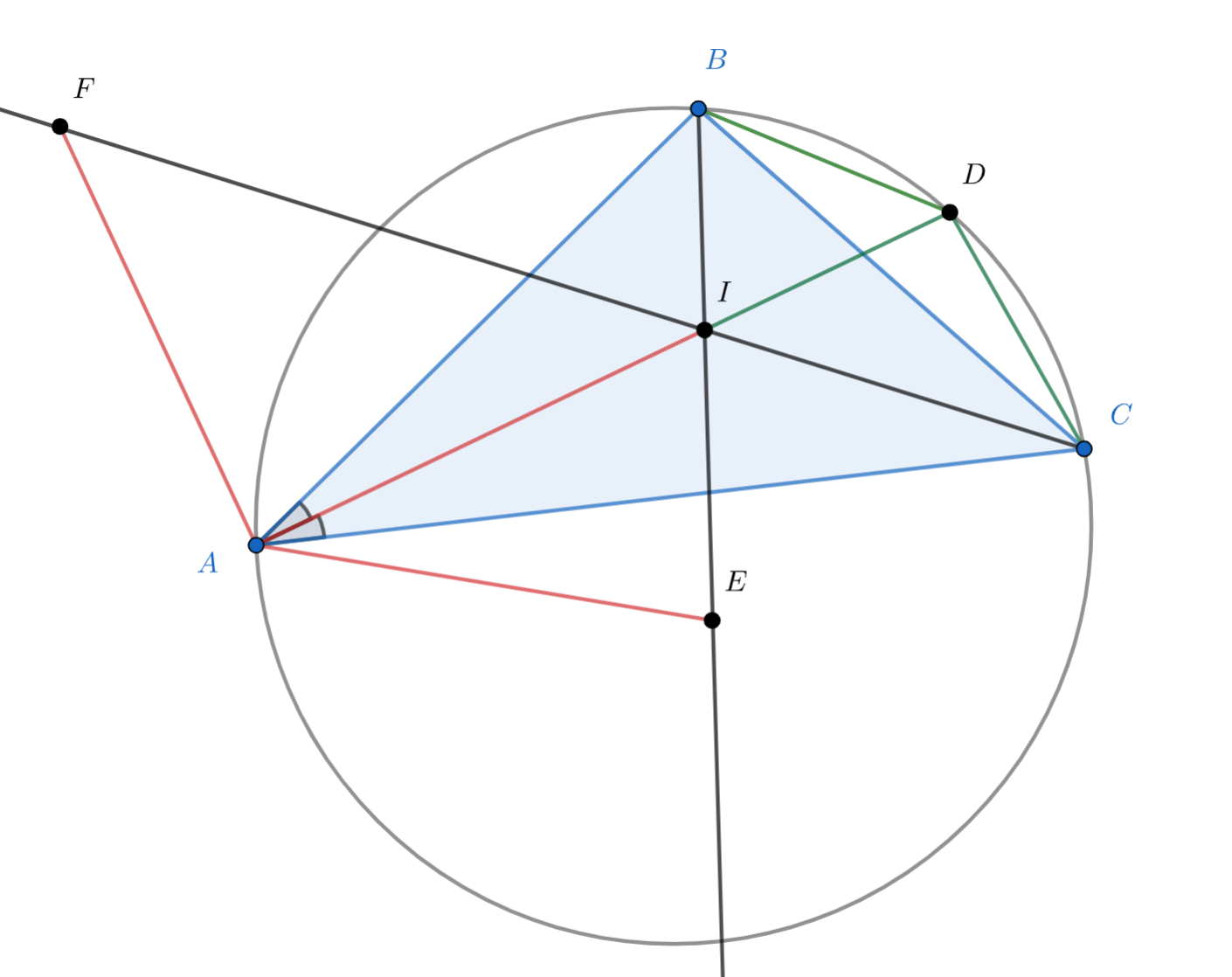
Рассмотрим точку $D$ — середину дуги $BC$ описанной окружности треугольника $ABC$ . По лемме о трезубце $DB = DC = DI$ . Треугольники $DBI$ и $AEI$ подобны, так как это равнобедренные треугольники с равными углами при основании (углы в точке $I$ равны как вертикальные, потому что точки $A, I$ и $D$ лежат на одной прямой — биссектрисе угла $A$ ). Аналогично подобны треугольники $DCI$ и $AFI$ .

Отсюда получаем

BI= DI-= CI- EI AI FI

(первое равенство из первого подобия, второе — из второго). Раскрывая пропорцию, имеем $BI⋅FI = CI ⋅EI$ . Из этого равенства следует требуемое равенство площадей треугольников $BIF$ и $CIE$ , поскольку углы при вершине $I$ в треугольниках $BIF$ и $CIE$ равны как вертикальные.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#68313

Дан треугольник $ABC,$ точка $I$ — центр вписанной окружности, точка $A 1$ взята таким образом, что точка $A$ является серединой отрезка $A1I.$ Докажите, что точка $A1$ и центры вневписанных окружностей треугольника $ABC$ лежат на одной окружности.

Источники: ИТМО-2016, 9.8 (см. olymp.itmo.ru)

Подсказки к задаче

Подсказка 1

У нас есть условие, что A - середина отрезка IA₁, а также есть центры вневписанных окружностей...Какой можно использовать факт или теорему, где тоже какие-то точки являются серединами каких-то отрезков, причем этот факт или теорема связана с центрами вневписанных окружностей?)

Подсказка 2

Лемма о трезубце конечно! Если отметить середины дуг AB, BC и CA, то эти середины дуг являются серединами отрезков IC₁, IA₁ и IB₁ соответственно, где A₁, B₁, C₁ - центры вневписанных окружностей. У нас есть теперь достаточно много середин, которые завязаны на точке I...Что можно в этом случае сделать?

Подсказка 3

Посмотреть на сами серединки дуг и на точку A) Они все уже лежат на описанной окружности треугольника ABC, а дальше становится ясно что делать!

Показать доказательство

Докажем, что точки $A , D , E 1 1 1$ и лежат на одной окружности с центром в $O . 1$

$PIC$

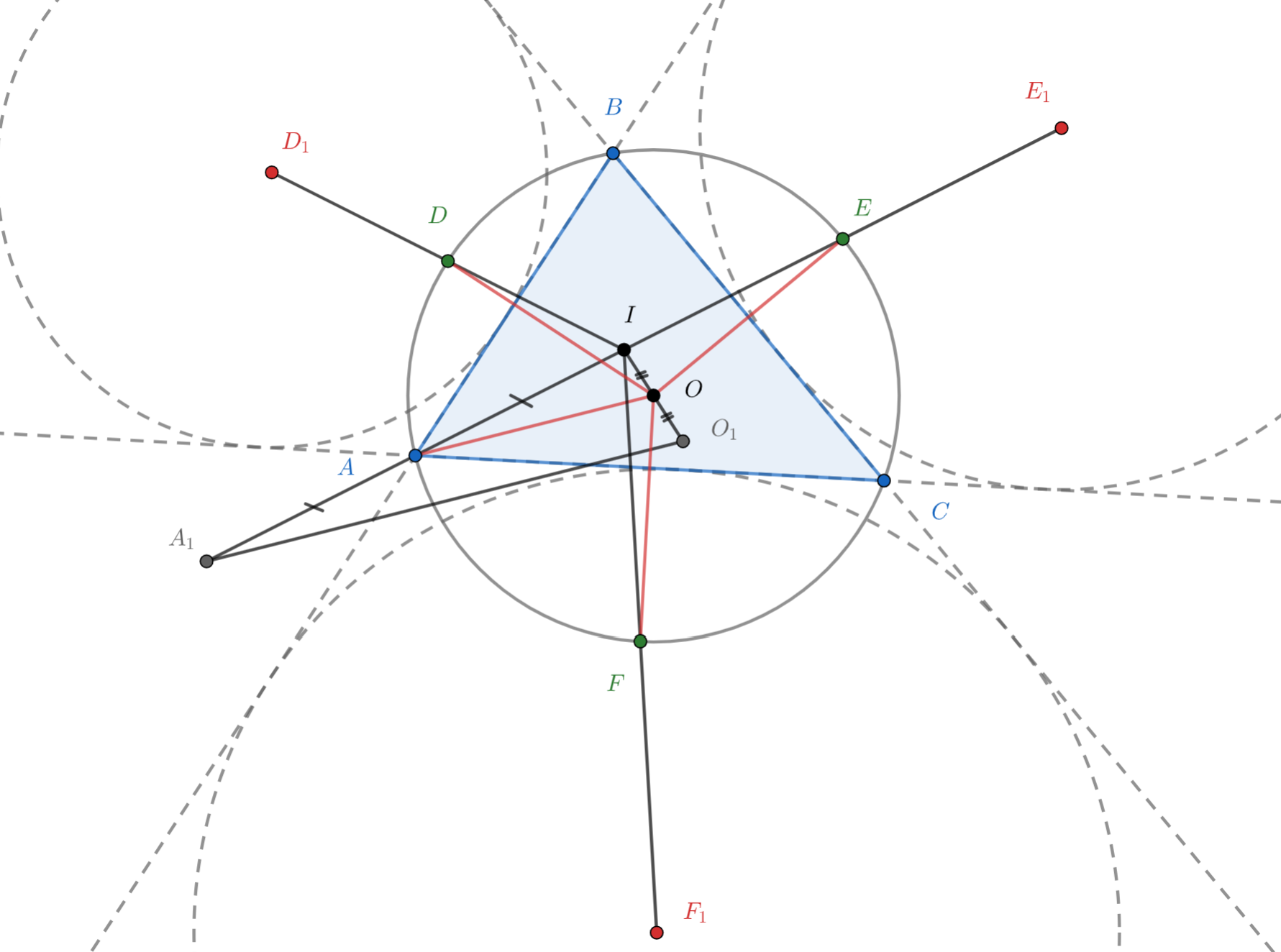
Пусть точка $O$ — центр описанной окружности треугольника $ABC$ ; $O1$ — такая точка, что $O$ середина $O1I$ ; точки $D, E$ и $F$ — середины дуг $AB, BC$ и $AC$ описанной окружности треугольника $ABC$ , а точки $D1, E1, F1$ — центры вневписанных окружностей треугольника $ABC$ , касающихся сторон $AB, BC$ и $AC$ соответственно. Тогда по лемме о трезубце точки $D, E$ и $F$ — середины $D1I, E1I$ и $F1I$ соответственно.

В треугольнике $A1O1I$ отрезок $AO$ является средней линией, значит $O1A1 = 2OA$ . Аналогичные равенства получаем и для остальных пар отрезков:

$D1O1 = 2OD, F1O1 = 2OF, E1O1 = 2OE$ и так как $OA =OD = OE = OF$ , получаем

O1A1 =O1D1 = O1E1 = O1F1

то есть точки $A1, D1, E1$ и лежат на одной окружности с центром в $O1$ , что и требовалось доказать. Заметим, что вместо последнего абзаца можно было применить преобразование подобия (гомотетию) с центром в точке $I$ и коэффициентом $2.$

Ошибка.
Попробуйте повторить позже

Задача 3#72122

Мальчик Вася выписал в тетрадку ненулевые коэффициенты многочлена $P (x)$ десятой степени. Затем у получившегося многочлена вычислил производную и выписал ее ненулевые коэффициенты, и так далее, пока не получилась константа, которую он также выписал. Какое наименьшее количество различных чисел у него могло получиться? Коэффициенты выписываются с учетом знака, свободные члены также выписываются, если имеется одночлен вида $n ± x$ , выписывается $±1.$

Подсказки к задаче

Подсказка 1

Раз уж многочлен P(x) имеет степень 10, то как минимум 1 ненулевой коэффициент у него есть! И стоит он перед... чем? Давайте обозначим его а и посмотрим на то, каким он становится при вычислении производных

Подсказка 2

Стоит он перед x¹⁰, конечно, а иначе у нас многочлен не 10 степени) При вычислении производных он умножается на соответствующую степень х, то есть на 10, 9, и т.д. до 0. Сколько ненулевых чисел получилось? Могли ли какие-то из них быть равны?

Подсказка 3

Конечно они не равны, а ведь не 0, получается как минимум 10 различных чисел у нас есть. Остаётся придумать пример!

Подсказка 4

Давайте просто возьмём тот многочлен, который рассматривали, когда придумывали оценку - а ⋅ x¹⁰, берём любое ненулевое а и побеждаем :)

Показать ответ и решение

Оценка: так как многочлен имеет степень $10$ , у него совершенно точно есть ненулевой коэффициент при $x10$ назовём его $a$ . Тогда старший коэффициент производной этого многочлена равен $10a$ , старший коэффициент второй производной равен $10 ⋅9a$ и т.д., старшие коэффициенты девятой и десятой производных равны $10!⋅a$ причем все эти числа, кроме двух последних, различны. Таким образом, $10$ различных чисел точно есть

Пример:

x10 x9 10! + 9! + ...x+ 1

даёт ровно 10 различных чисел, так как каждый следующий одночлен — производная предыдущего.

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 4#73448

Докажите, что для положительных $x,y,z$ выполняется неравенство

375 (x+ y+ z)(4x+ y+2z)(2x+ y+ 8z)≥ 2 xyz

Показать доказательство

Рассмотрим первые две скобки и заметим, что

2 2 (x +y+ z)(4x+ y+ 2z)= (2x+y) + 3z(2x+ y)+ 2z +xy

Тогда мы можем переписать требуемое неравенство в виде

(2x+-y)2+-3z(2x+-y)+2z2 2x+-y+8z- 375- ( xy +1)⋅ z ≥ 2

Теперь зафиксируем $z$ и $2x+ y$ и будем сдвигать $2x$ и $y$ друг к другу. При этом $xy$ увеличивается, и достигает максимума при $2x= y,$ остальные части выражения остаются постоянными. Значит, требуемое равенство будет следовать из неравенства, полученного подстановкой в него $y = 2x,$ то есть

(3x+ z)(6x+ 2z)(4x +8z)≥ 375x2z

Обозначим $x t= z,$ тогда неравенство превращается в

8(3t+ 1)2(t+ 2)− 375t2 ≥ 0

Взяв производную, можно убедиться, что минимум левой части достигается при $t= 43$ и равен $0,$ что доказывает требуемое неравенство. (таким образом, минимум исходного выражения достигается при $x:y :z = 4:8:3.$ )

Ошибка.
Попробуйте повторить позже

Задача 5#99086

Известно, что $x,y,z,t$ неотрицательные числа такие, что

xyz =1,y+ z+t= 2.

Докажите, что

2 2 2 2 x +y + z + t≥ 3.

Источники: ИТМО-2016, 9.7 (см. olymp.itmo.ru)

Подсказки к задаче

Подсказка 1

Давайте постепенно пытаться придумать, как пользоваться тем, что нам дали в условии(а может и не всё пригодится). В неравенстве, которое нам нужно доказать, фигурирует целых 4 переменных. Как можно попытаться избавиться от некоторых из них?

Подсказка 2

От квадратов довольно легко избавиться, потому что тогда выражение будет явно меньше. Но нужно, чтобы после этого осталось что-то хорошее. Давайте попробуем добавить что-то и вычесть для этого. Что это может быть?

Подсказка 3

Сначала давайте ещё внимательно посмотрим на неравенство. Справа у нас стоит тройка, но тогда, скорее всего, это результат применения неравенства о средних для трёх чисел. Давайте попробуем добавить и вычесть 2yz. Как это хорошо преобразуется?

Подсказка 4

Верно, тогда можно собрать (y-z)², а 2yz заменить на 2/x из равенства в условии. Давайте теперь вспомним вторую подсказку. К какому хорошему неравенству можно свести выражение?

Подсказка 5

Конечно, к x²+2/x(если убрать квадраты, то выражение будет точно не больше). Теперь остался последний шаг — это грамотно применить неравенство о средних.

Показать доказательство

Запишем выражение, для которого нам нужно доказать неравенство, и преобразуем его:

2 2 2 2 2 2 2 2 2 2 2 x + y +z + t =x + 2yz+ y − 2yz+ z +t = x +2yz+ (y− z) + t

По условию известно, что $xyz = 1.$ Тогда можем заменить $yz$ на $1. x$ К тому же будет верна следующая оценка:

2 2 2 2 2 2 x + x + (y− z) + t≥ x + x

Тогда запишем неравенство о средних в следующем виде:

1 1 ∘ ---1-1- x2 +x + x ≥ 3⋅ 3 x2⋅x ⋅x = 3

Итого получаем то, что нам нужно было доказать.