ШВБ 2020
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Для всех неотрицательных значений вещественной переменной функции
выполняется условие
Вычислите , если
.
Источники:
Подсказка 1
В равенстве из условия можно выразить f(x+1) через f(x). Кажется, это намекает на какую-то рекурсию, попробуем выразить f(x) через f(x-1) и т.д. Заметна ли какая-то закономерность?
Подсказка 2
Да, на самом деле для натурального n можно выразить f(n) через f(0) = 2020, получится равенство f(n) = 2020 - n + 43(1/(1×2) + 1/(2×3) + ... + 1/(n×(n+1))). Подумайте, как можно свернуть сумму дробей в скобках.
Подсказка 3
Попробуйте каждую дробь из суммы расписать как разность двух дробей так, чтобы при суммировании почти все члены сокращались.
Подсказка 4
1/(k(k+1)) = 1/k - 1/(k+1), тогда все члены сокращаются, кроме первого и последнего, получаем f(n) = 2020 - n + 43(1 - 1/(n+1)). Что можно применить, чтобы доказать эту формулу для любого натурального n?
Подсказка 5
Конечно же, индукцию! База легко проверяется, переход также несложно доказывается. Остаётся посчитать f(2020) :)
Докажем по индукции, что
_________________________________________________________________________________________________________________________________________________________________________________
База очевидна:
_________________________________________________________________________________________________________________________________________________________________________________
Переход несложно доказать:
_____________________________________________________________________________________
Таким образом, по доказанной формуле
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Вот как прийти к решению:
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение выражения
если — произвольная квадратичная функция, удовлетворяющая условию
и принимающая неотрицательные
значения при всех действительных
Источники:
Подсказка 1
Давайте не побоимся и подставим вместо f(1), f(0) и т.д. их настоящие значения через a, b, c и вспомним, когда квадратных трёхчлен принимает только неотрицательные значения?
Подсказка 2
Верно, при a > 0, D <= 0, это даёт нам оценку на c и a, как бы нам это использовать?
Подсказка 3
Можно заметить, что там, где есть множитель b, модуль степени a на 1 меньше, может быть получится сделать какую-нить замену?
Подсказка 4
Да, можно вынести a (a > 0) и сделать замену t = a/b, а у выражения относительно t мы легко можем найти точки минимума. Остаётся только ...
Подсказка 5
Проверить, что этот минимум достигается
Имеем
Тогда исходное уравнение принимает вид
Поскольку — произвольная квадратичная функция, принимающая неотрицательные значения при всех
действительных
то
Тогда
где
Рассмотрим функцию и найдем ее наименьшее значение при
при производная
равна
и, проходя через эту точку, меняет знак с «минуса» на «плюс», следовательно,
Ошибка.
Попробуйте повторить позже
Решите систему уравнений
Источники:
Подсказка 1
Хм, в обоих уравнениях слева есть общий множитель. Что можно с этим сделать?
Подсказка 2
Да, можно выразить/поделить одно уравнение на второе и аналогичные действия. Тогда получим соотношение между x и y, а значит, подставив его в одно из уравнений, получим квадратное и решим его, не забудем посчитать и вторую переменную!
Разделим первое уравнение системы на второе:
Подставим в уравнение:
Ошибка.
Попробуйте повторить позже
Окружность проходит через вершины и
равнобедренного треугольника
и пересекает стороны
и
в точках
и
соответственно.
хорда этой окружности, равная по длине
содержит точку
лежащую на
и являющуюся основанием высоты треугольника
Прямая, проходящая через точку
и
перпендикулярная
пересекает прямую
в точке
Найти радиус окружности, описанной около треугольника
если
Источники:
Подсказка 1
Что можно сказать о четырёхугольнике AMNC?
Подсказка 2
AMNC — равнобокая трапеция! Было бы полезно найти окружность, на которой лежать точки K, M, L. Например, найти вписанный четырёхугольник, вершинами которого являются эти точки. Какие есть подозрения на четвёртую вершину?
Подсказка 3
Давайте попробуем доказать, что BMKL — вписанный! Равенство каких углов нам для этого нужно?
Подсказка 4
Попробуем доказать, что углы MBK и MLK равны! Очень часто помогает идея разбить нужные углы на части, а затем доказать попарное равенство частей.
Подсказка 5
Что можно сказать о треугольниках CBH и NLC?
Подсказка 6
Треугольники CBH и NLC подобны! Тогда можно будет выписать соответствующие отношения сторон и попробовать найти другие подобные треугольники!
Подсказка 7
Рассмотрите треугольники KCL и BHK. Можно можно сказать про отношение их сторон? А о тупых углах в них?
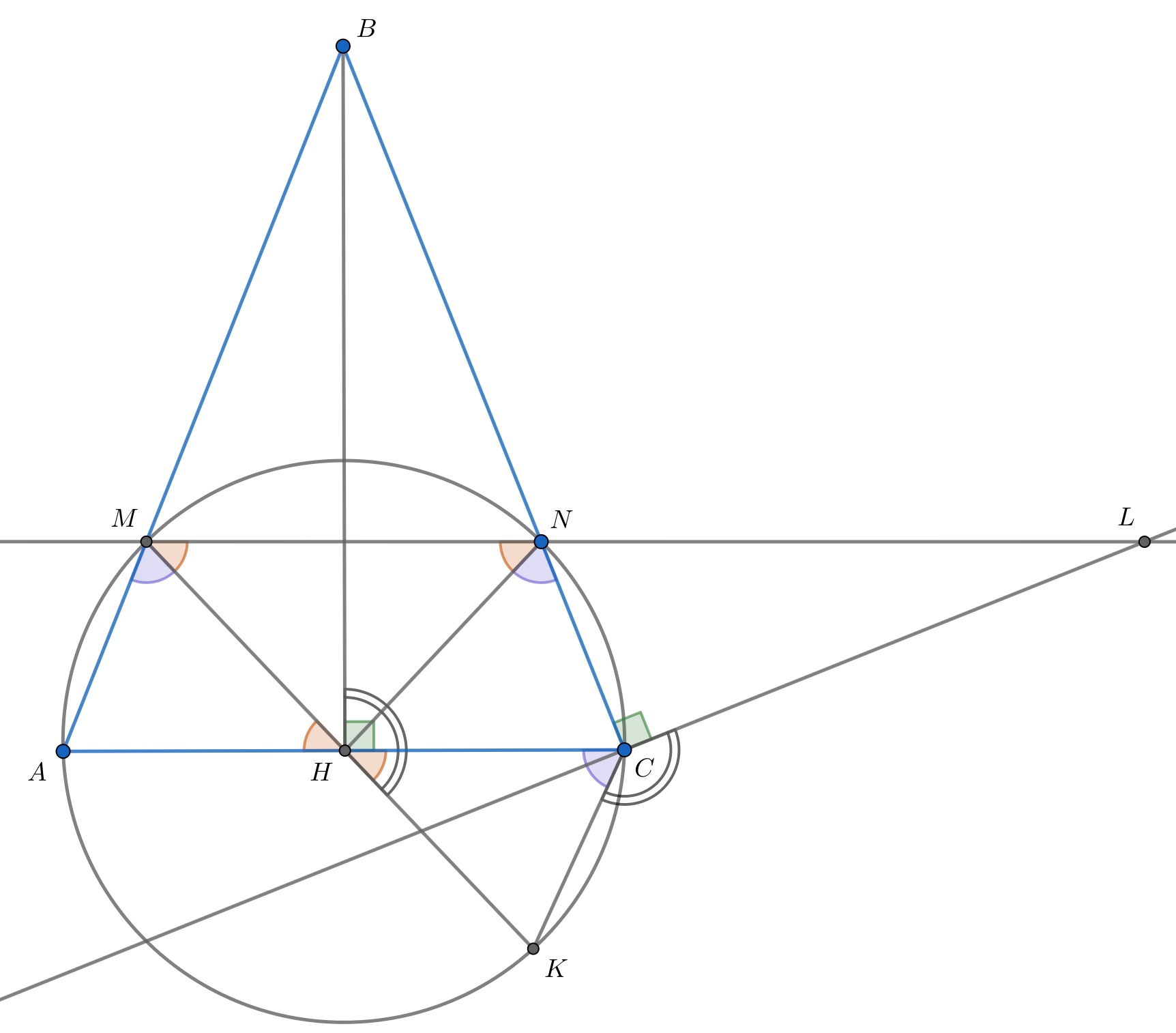
Четырехугольник — равнобедренная трапеция. Треугольники
и
равны по двум сторонам и углу между ними.
Тогда:
(как углы равных треугольников и как углы, опирающиеся на одну дугу). Следовательно, треугольник подобен треугольнику
и треугольник
подобен треугольнику
по двум углам. Значит,
и учитывая, что , получаем подобие треугольника
и треугольника
следовательно,
а значит, точки лежат на одной окружности и
Ошибка.
Попробуйте повторить позже
Четыре лифта небоскреба, отличающиеся цветовой гаммой (красный, синий, зеленый и желтый) движутся в разных направлениях и с разной, но постоянной скоростью. Наблюдая за лифтами, некто включил секундомер, и, глядя на его показания, стал записывать: 36-я секунда — красный лифт догнал синий (двигаясь с ним в одном направлении). 42-я секунда — красный лифт разминулся с зеленым (двигаясь в разных направлениях), 48-я секунда — красный лифт разминулся с желтым, 51-я секунда — желтый лифт разминулся с синим, 54-я секунда — желтый лифт догнал зеленый лифт. На какой секунде от начала отсчета зеленый лифт разминется с синим, если за период наблюдения лифты не останавливались и не меняли направления движения?
Источники:
Подсказка 1
В задаче описано много величин, поэтому записывать все уравнения и решать их не хочется. Скорость движения лифтов постоянна, поэтому графиком координаты от времени будет являться прямая.
Подсказка 2
Без ограничения общности можно считать, что красный лифт едет наверх. Тогда направления остальных лифтов определяются однозначно. Теперь нужно использовать геометрические соображения.
Подсказка 3
Времена из условия имеют чёткую связь между собой: 42 = (48+36)/2 и 51 = (48 + 54)/2. Мы много знаем про чевианы, которые делят сторону треугольника в отношении 1:1. Теперь нужно понять, координата по времени какой точки в треугольнике нас интересует.
Занумеруем лифты: красный — первый, синий — второй, зеленый — третий, желтый — четвертый. Лифты движутся с постоянными
скоростями, следовательно, для каждого лифта пройденное расстояние в некоторой системе координат зависит от времени
по закону.
По условию задачи красный и синий лифт движутся в одном направлении, причем красный догоняет синий, следовательно:
Пусть тогда и
Зеленый и желтый лифты движутся в противоположном направлении с двумя первыми, и желтый догоняет зеленый, следовательно:
Построим графики функций согласно условию задачи.
![]()
Нужно определить абсциссу точки Точка
— точка пересечения медиан треугольника
Воспользуемся теоремой
Фалеса:
на 46 секунде
Ошибка.
Попробуйте повторить позже
Найдите все натуральные числа для которых число
является квадратом натурального числа.
Источники:
Подсказка 1
В точный квадрат все простые множители входят в чётных степенях. В нашей задачей рассматривают сумму, которая содержит степени двойки, так что можно рассмотреть именно степень вхождения двойки.
Подсказка 2
Попробуем провести разумный перебор. Допустим, самая маленькая степень вхождения двойки в слагаемые будет в 3*2ⁿ. Тогда она должна быть чётной, мы можем явно проверить эти случаи.
Подсказка 3
Пусть теперь n достаточно большое. Тогда можно вынести 2¹⁰, останется какая-то нечётная сумма, которая должна быть равна (2k+1)² для какого-то k.
Подсказка 4
После раскрытия скобок можно будет сократить на 4, а после разложить на множители. Остаётся заметить, что скобки, связанные с k, имеют разную чётность, а значит, одна из них гарантированно маленькая.
Рассмотрим несколько случаев
1) Пусть тогда
второй сомножитель — нечетное число,
- Если
то
не является квадратом натурального числа.
- Если
то
не является квадратом натурального числа.
- Если
то
не является квадратом натурального числа.
- Если
то
не является квадратом натурального числа.
2)
- Пусть
тогда
не является квадратом натурального числа.
- Пусть
тогда
не является квадратом натурального числа.
- Пусть
тогда
не является квадратом натурального числа.
3) Пусть тогда
и
Числа и
разной четности, следовательно, одно из них является делителем 3. Поскольку
, то либо
,
либо
13, 15
Ошибка.
Попробуйте повторить позже
В треугольнике проведена биссектриса
Известно, что центры вписанной в треугольник
и описанной около треугольника
совпадают. Найдите
если
Ответ не должен включать обозначения тригонометрических функций и обратных к
ним.
Подсказка 1
На картинке есть центр вписанной окружности, давайте тогда попробуем посчитать углы! Пусть угол ∠A=α, ∠B=β. Какие углы на картинке можно выразить через них?
Подсказка 2
Посчитайте ∠BAO и ∠ABO. Посмотрите, теперь мы можем выразить один через другой, использовав условие! Быть может, выразим через углы α и β все углы треугольника ABC?
Подсказка 3
α = 2β, то есть в равнобедренном треугольнике у нас один угол в два раза больше другого. Тогда несложно найти их все!
Подсказка 4
Нам нужно найти CD, который по сути является одним из отрезков, на которые делит биссектриса угла противоположную сторону! Каким свойством можно воспользоваться для поиска этого отрезка?
Подсказка 5
Хотелось бы воспользоваться свойством биссектрисы про отношение сторон треугольника! Но перед этим было бы хорошо выразить BD и AC (чтобы уравнение решалось). А что можно сказать про треугольники ABD и ADC? ;)
Пусть Точка
— центр вписанной в треугольник
окружности. Тогда
так как центр вписанной окружности лежит на биссектрисе. Поскольку — центр описанной вокруг
окружности, то треугольник
равнобедренный. Следовательно,
![]()
Треугольники и
равнобедренные, и
Поскольку
Так как
то треугольник равнобедренный, а
Пусть Треугольники
и
подобны по трём углам:
По условию поэтому
2
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при котором для любого значения параметра
неравенство
не выполняется хотя бы для одного значения
Источники:
Подсказка 1
Выражения, связанные с x, являются тригонометрическими функциями, так что полезно сделать замену cos 2x = y. Тогда мы знаем, какие значения принимает y, и при этом избавились от косинусов.
Подсказка 2
У нас получается парабола от y с ветвями вверх. Нас интересует её минимум на отрезке: он будет или на границе отрезка, или в вершине параболы. Это позволяет получить какие-то системы неравенств.
Подсказка 3
Теперь задачу можно изобразить на графике в осях aOb, поскольку у нас как раз 2 параметра. Тогда значения параметров, для которых существует хотя бы один плохой y, лежат внутри пересечения графиков.
Подсказка 4
Нас интересуют такие b, что весь отрезок [-2; 1] будет лежать в области внутри графиков. Осталось подставить крайние значения для a и получить ответ.
Пусть Тогда:
Найдем при каких и
неравенство выполняется для любых
Рассмотрим функцию
Ее графиком является парабола с ветвями вверх и вершиной в точке Рассмотрим три случая местоположения
вершины относительно отрезка
На координатной плоскости изобразим множество точек
удовлетворяющих всем трём условиям. Точки, для которых
неравенство не выполняется хотя бы для одного
, лежат внутри области, ограниченной графиками. Проверим область на
замкнутость:
![]()
Точки пересечения графиков и
Точки пересечения графиков и
Аналогично проверяем точки пересечения графиков с Точки совпадают, значит, область замкнутая.
В итоге, точки, для которых неравенство не выполняется хотя бы для одного
образуют
замкнутую область, граница которой состоит из графиков двух окружностей и гиперболы, граница включается. Для решения задачи
необходимо найти такие значения
при которых точки
попадают в получившуюся область для любых
Такие значения
образуют отрезок
найдем, подставив
в уравнение гиперболы.
найдем, подставив
в уравнение окружности
Получаем
Ошибка.
Попробуйте повторить позже
Основанием пирамиды является ромб
Высота пирамиды
равна 1, точка
лежит на прямой, содержащей
диагональ основания
причем
Боковое ребро
равно
а боковые грани наклонены к плоскости основания
под углами
и
Найдите длину стороны основания и угол между боковым ребром
и плоскостью боковой грани
Источники:
Подсказка 1
Чтобы найти сторону основания, нужно собрать про него побольше информации. Нам даны углы наклона боковых плоскостей к основанию, а также длина высоты. С помощью этого можно найти длины некоторых отрезков в основании, используя теорему о трёх перпендикулярах.
Подсказка 2
Проведите перпендикуляр из K к прямым AB и DC. Обозначьте точки пересечения с ними M и N. Как раз там и будут углы между боковыми плоскостями и основанием. Теперь вы можете легко посчитать KM, KN, CK. А дальше небольшой счёт в ромбе даст вам длину стороны.
Подсказка 3
Давайте теперь построим угол между TA и TCD. Для этого нам нужен перпендикуляр из точки A на плоскость TCD. Пусть FA || TK и F лежит на TC, а AL || DC и L лежит на MC. Может поискать его в плоскости AFL?
Обозначим точки пересечения прямых и
с перпендикуляром из точки
к этим прямым за
и
соответственно.
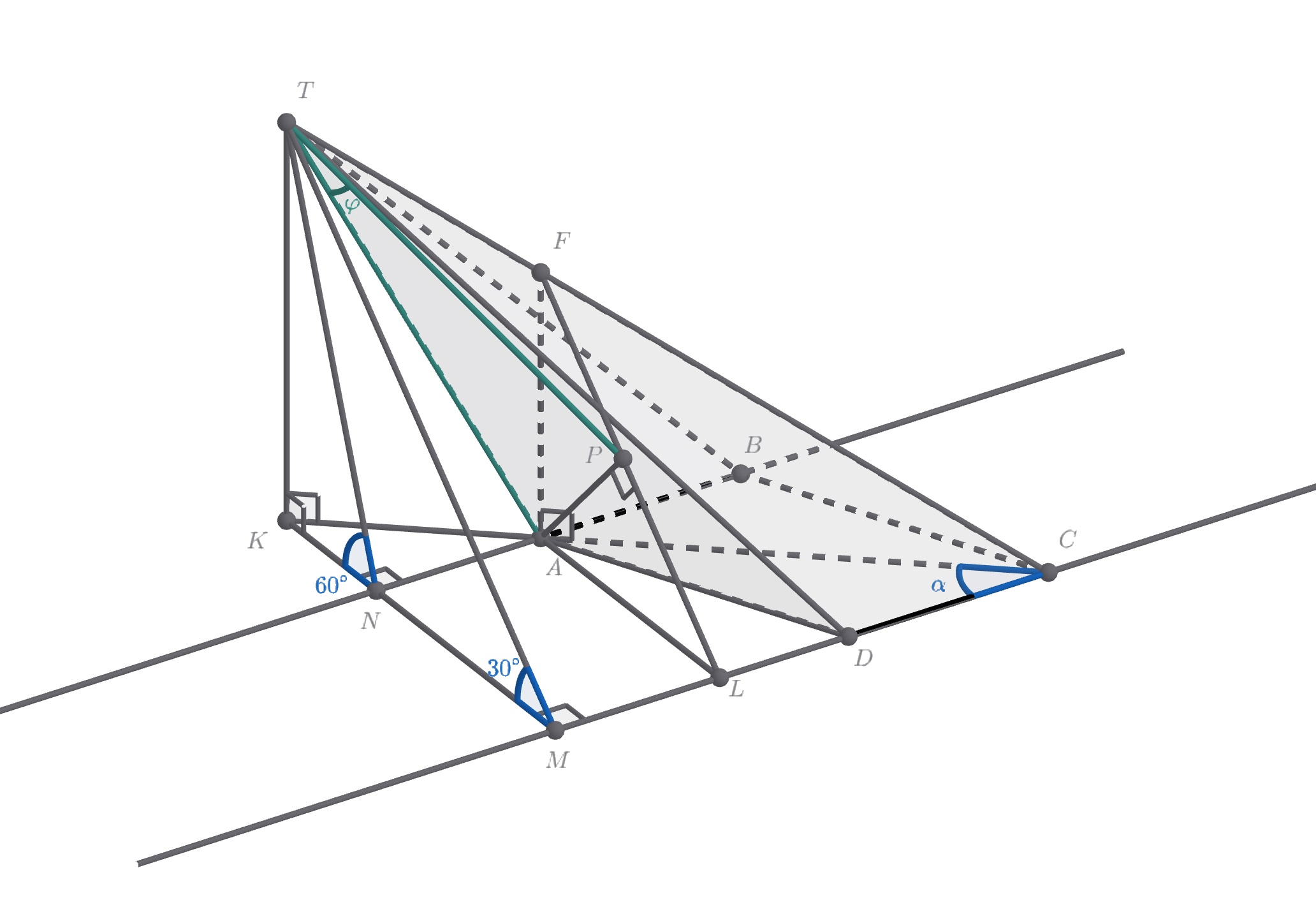
Тогда, так как угол и
— перпендикуляр к плоскости основания, получаем. что
Аналогично для угла
Так как треугольник прямоугольный с гипотенузой
то по теореме Пифагора
Аналогично для треугольника
Пусть тогда
По формуле синуса двойного угла получим
Тогда сторона основания равна
Откуда получаем
Так как то
Проведем так как
то
откуда получим
Построим перпендикуляр Так как
— прямоугольник, то
Из прямоугольного треугольника получаем
Построим — проекция
на плоскость
угол
— искомый угол.
тогда
Ошибка.
Попробуйте повторить позже
Решите неравенство
Подсказка 1
Посмотрите внимательно на нашу дробь: что можно сказать про знак её числителя?
Подсказка 2
Верно, он неотрицателен. А когда дробь с неотрицательным числителем является неположительной?
Подсказка 3
Да, либо когда её числитель равен нулю, либо когда знаменатель отрицателен. Осталось только разобрать два этих случая. Не забудьте про ОДЗ!
Для начала распишем ОДЗ:
Числитель дроби неотрицателен, так как является суммой двух модулей. Тогда, для того, чтобы дробь была не положительной, нужно, чтобы либо знаменатель был не положительным, либо числитель был равен нулю. Поэтому, с учетом ОДЗ, получим совокупность:
Решим первое неравенство:
Теперь решим уравнение из рассматриваемой совокупности. Оно имеет решение тогда и только тогда, когда каждый модуль равен 0 :
Решим первое уравнение:
Подставляя и
во второе уравнение системы, видим, что они являются его корнями:
Но не ответ по ОДЗ, а
является решением системы, а, значит, и решением исходного неравенства.
Таким образом,


