Тема ШВБ - задания по годам

ШВБ 2018

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела швб - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#69859

Ваня и Дима пошли на рынок. У Вани было $1000$ рублей, а у Димы — $2000$ рублей. Они покупали что-то независимо друг от друга, а в какой-то момент они встретились и решили купить модель танка за $1800$ рублей. Найдите вероятность того, что оставшейся у них суммы хватит на это. Замечание. Условие нужно понимать так: у обоих мальчиков в момент встречи равновероятно может оказаться любое количество рублей, не превосходящее исходной суммы.

Источники: ШВБ-2018, 9.3 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

Давайте отобразим количество денег у ребят на координатной плоскости! То есть, по х отметим количество денег у Вани, а количество денег у Димы по y. Тогда с помощью координат каждой точки внутри прямоугольника (который образован исходным количеством денег у ребят) - мы можем посчитать количество денег, которое осталось у ребят!

Подсказка 2

Да, тогда мы можем сказать что у нас получился прямоугольник 5x10(так как у одного денег в два раза больше, чем у другого, то есть единичный отрезок равен 200 рублей). Тогда какие точки внутри этого прямоугольника нам подойдут?

Подсказка 3

Верно, все точки, координаты которых в сумме не меньше 9! То есть, все точки нужные нам лежат над прямой y=9 - x. Осталось посчитать площадь трапеции, лежащей над этой прямой и найти отношение полученной площади к площади прямоугольника!

Показать ответ и решение

Визуализируем вероятности на координатной плоскости. Заметим, что, взяв в качестве длины одного деления $200,$ мы можем считать, что равновероятно находимся в каждой точке прямоугольника размера $5 ×10ABCD$ (или размера $1000× 2000$ ).

$PIC$

Нас интересует, когда $x +y ≥1800$ — на нашей плоскости это не ниже прямой $x +y = 9.$ Нетрудно посчитать, что она пересекает прямоугольник в точках $E(0,9),T(4,5).$ Тогда итоговый ответ можно найти, как отношение площадей

p= STEBC-= 1+26⋅5 =0.35 SABCD 50

Ответ:

$0,35$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#70301

Решите уравнение

4 2019 2018 sin (2025x)+ cos (2016x)⋅cos (2025x) =1

Источники: ШВБ-2018 (см. olymp.bmstu.ru)

Показать ответ и решение

ОТТ: $sin2(2025x)+cos2(2025x)= 1$

Чтобы из ОТТ получить исходное, нужно домножить первое слагаемое на $2 sin (2025x)$ , а второе на $2016 2019 cos (2025x)⋅cos (2016x)$ . Заметим, что при этом левая часть точно не увеличилась. Следовательно, чтобы сохранилось равенство, возможны только следующие случаи:

Либо одно из слагаемых 0 и тогда не важно, на что его домножаем, но важно, чтобы другое слагаемое было равно 1 и домножилось на 1. Либо домножили оба слагаемых на 1.

$2 2 1)1+ 0= 1.Заметим, чтоsin(2025x)= 1 при cos (2025x)=0.$ Поэтому имеем:

π πk cos(2025x)=0 ⇔ x= 4050 + 2025

$2)0+ 1= 1:$

{ { { cos2016(2025x)⋅cos2019(2016x)= 1 ⇔ cos(2025x)=±1 ⇔ 2025x= πn,n ∈ℤ ⇒ cos2(2025x)= 1 cos(2016x)=1 2016x= 2πk,k∈ ℤ

⇒ 2025k= 1008n⇒ k ...1008⇒ k =1008t,t∈ ℤ

Подставим в систему, получим: $x = πt.$ Проверим, что подходит:

2025πt= πn⇔ n = 2025t,n∈ ℤ

3) Оба слагаемых домножили на 1:

{ sin2(2025x)= 1 cos2019(2016x)⋅cos2016(2025x)= 1

sin2(2025x)= 1⇒ cos(2025x)= 0

Система не имеет решений.

Ответ:

${-π-+ -πk,πk,k ∈ℤ} 4050 2025$

Ошибка.
Попробуйте повторить позже

Задача 3#85349

Найдите все такие $k$ и $b$ , при которых система уравнений

{ y+2|x|= 2; y = kx +b

имеет бесконечно много решений.

Подсказки к задаче

Подсказка 1

Построим график функции, соответствующей первому уравнению, он без параметра, никуда не двигается. А вторая функция может задавать любую прямую.

Подсказка 2

Прямая может пересекать галочку в бесконечном числе точек, только если прямая совпадает с одной из “половинок” этой галочки. Осталось всего лишь выписать уравнения прямых, соответствующих двум половинкам галочки и выразить оттуда k и а.

Показать ответ и решение

Посмотрим на график первого уравнения. Это галочка с вершиной в точке $(0;2)$ , пересекающая ось $OX$ в точках $(−1;0)$ и $(1;0).$

$PIC$

Уравнение $y = kx+ b$ задает прямую. Предположим, что $k$ отлично от $2$ и $− 2.$ Тогда прямая непараллельна ни одному из лучей графика первого уравнения, и поэтому пересекает его не более, чем в двух точках.

Если $k= 2,$ то прямая либо содержит левый луч графика модуля, либо параллельна ему, а также имеет не более одной общей точки с правым лучом. Бесконечное число решений получится, если прямая содержит левый луч графика. Это происходит при $b= 2,$ так как тогда точка $(0;2)$ принадлежит прямой.

Аналогично при $k =−2$ получаем $b =2.$

Ответ:

$k =2;b= 2$ или $k =− 2;b= 2.$

Ошибка.
Попробуйте повторить позже

Задача 4#88134

Найдите наименьшее натуральное число, имеющее ровно 42 натуральных делителя (включая единицу и само число).

Подсказки к задаче

Подсказка 1

Подумаем, а что мы вообще знаем о количестве делителей?

Подсказка 2

Количество делителей равно произведению степеней, в которых простые числа входят в число (пусть M), увеличенных на единицу! Тогда рассмотрим разложение M и составим уравнение по условию!

Подсказка 3

Пусть простые делители входят в M в степенях k₁, k₂, …, kₙ. Тогда (k₁+1)(k₂+1)…(kₙ+1) = 42. Остается лишь разобрать случаи ;)

Показать ответ и решение

Пусть $n$ — искомое натуральное число, разложим на простые:

k1 k2 km n =p1 ⋅p2 ⋅...⋅pm

Любой натуральный делитель этого числа имеет вид

l1 l2 lm d= p1 ⋅p2 ⋅...⋅pm

где $li ∈{0,1,...,ki},i= 1,...,m$ . Число делителей числа $n$ равно

(k1+1)(k2+1)⋅⋅⋅(km+ 1)= 42.

Разложим число 42 на неединичные сомножители всеми возможными способами и выберем из них наименьшее $n.$ Поскольку $42= 2⋅3⋅7$ , то имеем пять случаев:

1) $42 =42$ , наименьшее число $n =241 > 3000$ ;

2) $42 =21⋅2$ , наименьшее число $n =220⋅31 >3000$ ;

3) $42 =14⋅3$ , наименьшее число $n =213⋅32 >3000$ ;

4) $42 =7⋅6$ , наименьшее число $n =26⋅35 = 64⋅243 >3000$ ;

5) $42 =7⋅3⋅2$ , наименьшее число $n =26⋅32⋅51 = 2880$ .

Ответ: 2880

Ошибка.
Попробуйте повторить позже

Задача 5#97397

Найдите площадь сечения правильной треугольной призмы $ABCA B C 1 1 1$ плоскостью, которая параллельна диагонали $AC1$ боковой грани $AA1C1C,$ проходит через середину стороны $AB$ основания $ABC$ и точку $M,$ лежащую на стороне $B1C1,$ если, $MC1 =3B1M,$ расстояние между $AC1$ и секущей плоскостью равно $3,$ а сторона основания призмы равна $√-- 2 14.$

Подсказки к задаче

Подсказка 1

Попробуйте сначала построить само сечение (через параллельные прямые) и понять, что за фигура получается в сечении.

Подсказка 2

Правильно, в сечении получается трапеция. Для нахождения площади сечения можем использовать теорему о площади ортогональной проекции. Проекцию на какую плоскость удобнее всего рассматривать?

Подсказка 3

Рассматриваем проекцию на плоскость основание призмы. Как мы можем найти её площадь?

Подсказка 4

Находим площадь проекции как разность площадей двух треугольников, её составляющих (очевидно, как из этого получается площадь трапеции). Что теперь нам нужно найти для применения теоремы из подсказки 2?

Подсказка 5

Нужно найти косинус угла наклона плоскости сечения к плоскости основания призмы. Для этого нужно построить дополнительную плоскость, проходящую через B перпендикулярную линии пересечения двух плоскостей. Строим в ней прямоугольный треугольник и находим необходимый косинус угла!

Показать ответ и решение

В плоскости основания $ABC$ проводим прямую $EA,$ параллельную $B C 1 1$ , $EA = MC 1$ , и прямую $ME,$ параллельную $AC ,ME 1$ лежит в плоскости сечения. В плоскости основания $ABC$ проводим прямую, соединяющую точку $E$ с серединой $D$ стороны $AB$ , точка $K$ — точка пересечения этой прямой со стороной $BC$ . В плоскости основания $A1B1C1$ проводим прямую $MN$ , параллельную $DK.$ Точка $N$ — точка пересечения прямой $MN$ со стороной $A1B1.$ Трапеция $DKMN$ — искомое сечение.

$PIC$

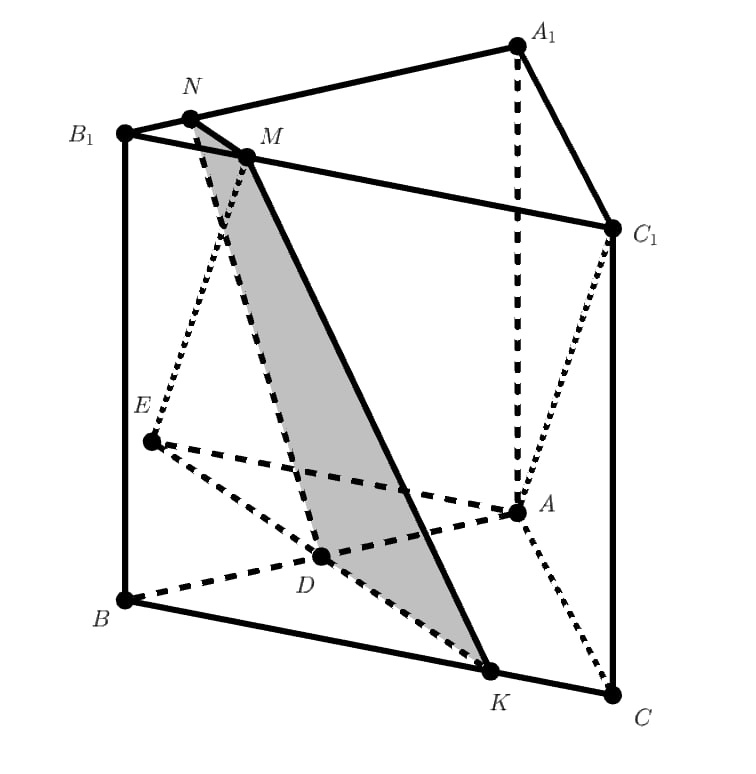
Найдём площадь проекции сечения на плоскость основания призмы. Обозначим сторону основания через $a$ . Тогда $BK = EA = MC1 = 34a,BD = a2$ . Пусть $Q$ — проекция точки $M$ на основание $ABC,BQ = a4$ . Пусть $G$ — проекция точки $N$ на основание $ABC$ . Поскольку $GQ$ и $DK$ параллельны, то $BQ :BK = BG :BD$ , и $BG = a6$ . Проекцией сечения на плоскость основания $ABC$ является трапеция $DKQG$ , её площадь

( ) 2√- √- Sпр = SBDK − SBGQ = SABC 3⋅ 1 − 1⋅ 1 = 1SABC = a-3 = 14-3 4 2 4 6 3 12 3

$PIC$

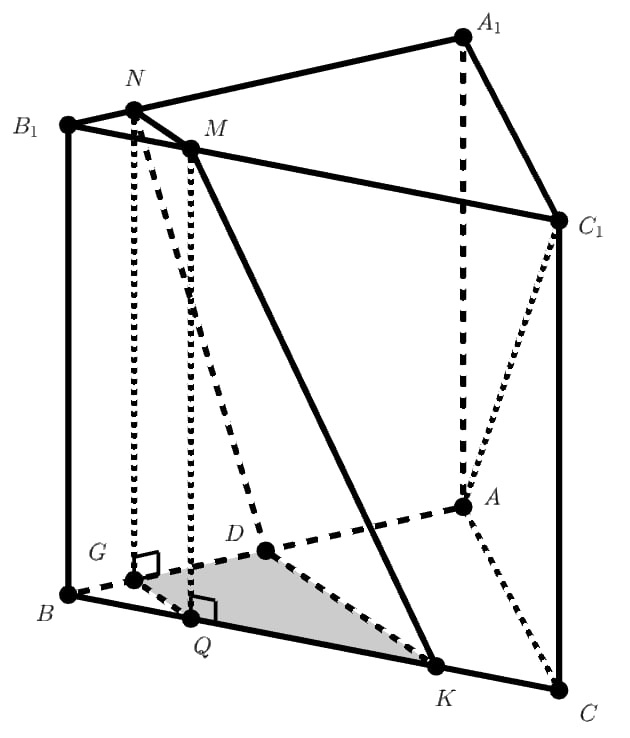
Найдём косинус угла $α$ наклона плоскости сечения к плоскости основания призмы. Расстояние $d$ от прямой $AC1$ до плоскости сечения равно расстоянию от точки $A$ до плоскости сечения, которое, в свою очередь, равно расстоянию от точки $B$ до плоскости сечения (так как $AD = DB$ , $D$ принадлежит плоскости сечения).

Построим плоскость $BHF,$ проходящую через точку $B$ и перпендикулярную $DK$ линии пересечения основания и плоскости сечения ( $BH$ и $F H$ перпендикулярны $DK$ ). Проведем прямую $BP$ перпендикулярную $FH$ , тогда расстояние $d$ равно $BP :$

$PIC$

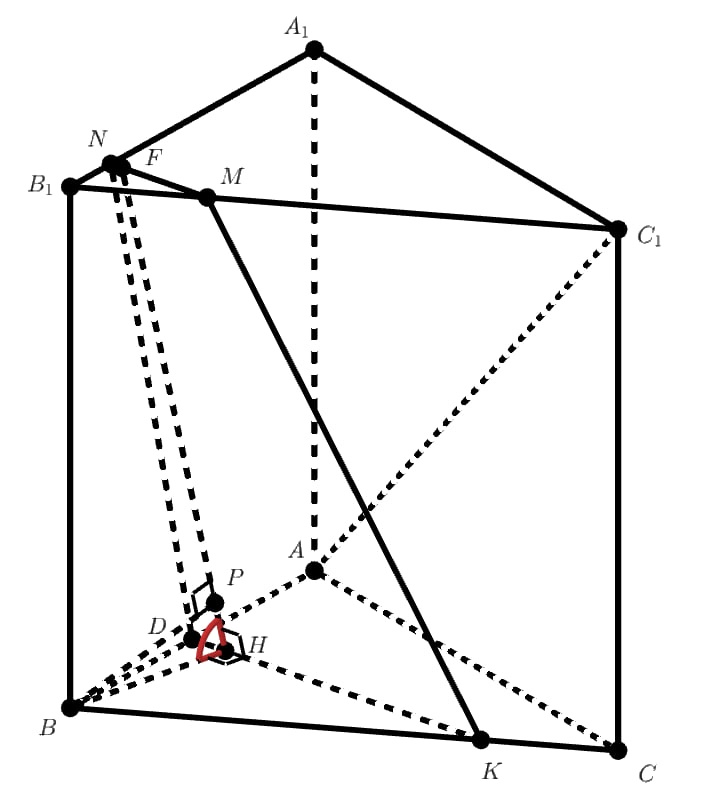
Угол наклона плоскости сечения к плоскости основания равен углу $BHL$ . Находим:

--------- ┌││ (--√-)2--(-)- √ - √- DK = ∘DQ2 + QK2 =∘ a-3- + a 2 = a-7= 7-2 4 2 4 2 BH ⋅DK = BD ⋅BK sin60∘ 3a√3 3√6- BH = -4√7- = -2-

В треугольнике $BPH$ имеем

sinα =-d- = 2√-- BH 6

-1- cosα= √ 3

Итого по теореме о площади ортогональной проекции

√ - √- Sсеч = Sпр-= 14-3⋅ 3= 14 cosα 3

Ответ: 14

Ошибка.
Попробуйте повторить позже

Задача 6#98979

Дима посадил в центре прямоугольного листа бумаги размером $15$ см на $20$ см круглую кляксу радиусом $2$ см. Сразу после этого Дима посадил ещё одну такую кляксу, которая также целиком оказалась на листе. Найдите вероятность того, что эти две кляксы пересекаются.

Показать ответ и решение

Так как клякса имеет радиус $2$ см, следовательно центр кляксы будет расположен внутри прямоугольника $11$ см на $16$ см. Чтобы кляксы пересекались нужно чтобы расстояние между центрами двух клякс было не больше $4$ см. Тогда вероятность того, что вторая клякса будет пересекаться с первой будет равна:

π ⋅42 π 11⋅16 = 11

Ответ:

$-π 11$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#106820

Найдите все значения параметра $a$ , при каждом из которых система уравнений

{ log (ax)=2log (x+ y), 3−|x x−1=|∘x2-−-6x-+|xy−1+|8-

имеет единственное решение, и найдите это решение при каждом $a$ .

Показать ответ и решение

Второе уравнение равносильно системе

{ x≤ 3, x2− 6x+y +8 =x2− 6x+ 9.

Следовательно, можем подставить $y = 1$ в исходную систему, учесть ограничения и получить равносильную систему:

(|{ x2+ (2− a)x+ 1= 0, y = 1, |( −1< x ≤3,x⁄= 0,x ⁄=1,x⁄= 2.

Выясним, при каких значениях параметра $a$ уравнение $x2+(2− a)x +1= 0(∗)$ имеет единственное решение, если $− 1< x ≤3,x⁄= 0,x ⁄=1,x⁄= 2$ .

1) $D= a(a− 4),D= a(a− 4),x= a−22$ . При $a =0$ корень $x =− 1$ не подходит; при $a =4$ корень $x =1$ не подходит.

2) Выясним, при каких $a$ точки $x= 0,x =1,x= 2$ являются решениями уравнения (*).

$x= 0$ не является решением ни при каком $a$ ;

$x= 1$ является единственным решением уравнения $(∗)$ при $a =4$ ;

∗ x= 2 является решением ( ) при a= 4,5,

поскольку при подстановке $x = 2$ в уравнение (*) имеем $22+(2− a)2 +1= 0,2a= 9$ . Однако, при $a= 4,5$ уравнение (*) имеет второе решение $x= 0,5$ , удовлетворяющее поставленным условиям.

Следовательно, при $a= 4,5$ система имеет единственное решение $x= 0,5,y = 1$ .

3) Если дискриминант уравнения (*) больше нуля, то уравнение имеет два различных решения, но при условии $f(− 1)f(3)< 0$ , где $f(x)= x2 +(2− a)x+ 1$ , один корень будет посторонним, а один будет удовлетворять неравенству $− 1< x< 3$ . Имеем $f(−1)= a,f(3)=16− 3a$ , приходим к неравенству $a(16− 3a)< 0$ , и $a∈ (− ∞;0)∪(16∕3;+∞ )$ .

Если $a∈ (−∞; 0)$ , то

√ ------ x= a−-2+--a2− 4a 2

Если $a∈ (16∕3;+∞ )$ , то $√----- x= a−2−-a2−4a- 2$ .

4) Проверим случаи, когда $f(−1)= 0$ и $f(3)= 0$ . Первое равенство выполняется при $a =0$ , уравнение (*) не имеет решений, удовлетворяющих поставленным условиям. Второе равенство справедливо при $a= 16∕3$ . В этом случае уравнение (*) имеет вид $x2+ 10x+ 1= 0 3$ , и имеет два решения $x= 1∕3$ и $x =3$ , которые оба подходят.

Ответ:

$(1;1) 2$ при $a= 9 2$

$a−2+√a2−4a ( 2 ;1)$ при $a∈ (−∞; 0)$

$a−2−√a2−4a ( 2 ;1)$ при $(16 ) a∈ 3 ;+∞$

Ошибка.
Попробуйте повторить позже

Задача 8#107090

Решите неравенство

(|x− 5|−-|x−-1|)log4(6−-x) (9x− 12⋅3x+ 27)log3x ≤0.

Подсказки к задаче

Подсказка 1

Хотим в перспективе применить метод рационализации. Какие преобразования в таком случае нужно сделать?

Подсказка 2

Хотим представить 9^x - 12 * 3^x + 27 в виде произведения разностей 3^g - 3^f, а логарифмы — в виде разности логарифмов. Вспомним, что логарифм частного — это разность логарифмов, пользуемся этим для приведения к необходимому виду.

Подсказка 3

Теперь все множители имеют требуемый для применения метода рационализации вид. Не забываем, что его можно применять только на ОДЗ, так что находим его, а потом находим решения с помощью метода интервалов.

Показать ответ и решение

Найдём ОДЗ:

x > 0, 6− x >0, x ⁄= 1, x⁄= 2

x∈ (0;1)∪(1;2)∪ (2;6)

Запишем неравенство из условия в виде

(log4(6−-x)−-log41)(|x− 5|−-|x−-1|) ≤0 (3x− 9)(3x− 3)(log3x− log31)

На ОДЗ исходное неравенство по методу рационализации эквивалентно следующему

(5− x)(x − 5− (x− 1))(x− 5+ (x − 1)) ---------(x-− 2)(x-− 1)2-------≤ 0

(x−-5)(x−-3) ≤0 (x− 2)

По методу интервалов

x∈ (0;1)∪(1;2)∪ [3;5]

Ответ:

$(0;1)∪ (1;2)∪[3;5]$

Ошибка.
Попробуйте повторить позже

Задача 9#110248

Решите неравенство

√ - (− x2+81+ (x− 9)√x2+-6x−-27) ∘ x−-3- 1 x⋅ -9-− x2+-(x+3)√x2+-6x−-27 ⋅ x+-9 ≥ √x

Подсказки к задаче

Подсказка 1

Какими формулами можно воспользоваться, чтобы преобразовать числитель?

Подсказка 2

Воспользуемся формулой разности квадратов! Отлично, тогда можно будет разложить и числитель, и знаменатель на множители :) А что делать с подкоренным выражением?

Подсказка 3

Можно найти корни у подкрошенного выражения и также разложить его на множители ;) И тогда будет видно, как же можно сократить числитель и знаменатель, чтобы максимально упростить выражение!

Подсказка 4

После всех сокращений получаем, что (9-x)/(x+3) ≥ 1/x.

Подсказка 5

Домножьте обе части неравенства на x(x+3).

Показать ответ и решение

Подкоренное выражение $x2+ 6x− 27$ имеет нули

∘ 2----- x= −3± 3+ 27= −3± 6,

поэтому раскладывается на множители как $(x +9)(x − 3).$

C учётом ограничения $x> 0$ для существования правой части исходного неравенства получаем, что корень $∘ (x-+9)(x-− 3)$ определён при $x ≥3$ и равен $√x-+9⋅√x-− 3.$