Тема Курчатов - задания по годам

Курчатов 2025

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела курчатов - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#120650Максимум баллов за задание: 7

Дан прямоугольный треугольник с натуральными длинами сторон. Пусть $α$ — его острый угол, а угол $β$ таков, что $tg2β = tg3α.$ Докажите, что величина $tgβ$ рациональна.

Источники: Курчатов - 2025, 11.1 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Давайте обозначим катеты через p и q. Соответсвенно, тангенс будет равен p/q. Теперь попробуйте расписать тангенсы двойного и тройного углов.

Подсказка 2

Получилось что-то совсем неприятное, слева — выражение от tgβ, справа — выражение от p и q. Как насчёт того, чтобы обозначить это выражение через n и попытаться понять, при каких n уравнение относительно tgβ будет иметь рациональные корни?

Подсказка 3

Нетрудно заметить, что это уравнение относительно tgβ является квадратным. Значит, для его рациональности достаточно лишь проверить, что дискриминант является квадратом рационального числа. При проверке не забывайте, что гипотенуза тоже имеет рациональную длину!

Показать доказательство

Пусть катеты треугольника будут $p$ и $q,$ тогда $tgα= p. q$ По формулам двойного и тройного аргументов получаем следующие формулы:

2tgβ tgα(3− tg2α) p(3q2 − p2) 1−-tg2β-= tg2β =tg3α= --1−-3tg2α--= q(q2− 3p2) :=n

Значит, $tg2β +2ntgβ − 1= 0.$ Это уравнение имеет рациональные корни тогда и только тогда, когда дискриминант этого квадратного уравнения будет точным квадратом. Вычисляя дискриминант, находим

( ) D ∕4 =n2+ 1= p(3q2− p2) 2+ 1=-(p2+q2)3- q(q2− 3p2) p2(3q2− p2)2

Видно, что это число является квадратом рационального числа, поскольку гипотенуза тоже натуральное число, а значит, $2 2 p + q$ тоже точный квадрат.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#120652Максимум баллов за задание: 7

В некоторой школе все ребята увлекаются геометрией и состоят в различных геометрических клубах. Известно, что у любых двух клубов есть хотя бы один общий член. Докажите, что можно раздать школьникам циркули и линейки таким образом, чтобы у одного человека были и циркуль, и линейка, у каждого из остальных были или циркуль, или линейка (но не оба инструмента сразу), и в каждом клубе у его членов нашлись бы и циркуль, и линейка.

Источники: Курчатов - 2025, 11.2 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Попробуйте сначала придумать, в каком клубе должен оказаться человек с циркулем и линейкой.

Подсказка 2

Если в каком-то клубе только один человек, то, конечно, необходимо отдать именно ему циркуль и линейку. А может ли оказаться, что таких клубов больше одного?

Подсказка 3

Верно, не может, ведь тогда эти два клуба не имеют общих людей! А как можно раздать циркуль и линейку остальным людям?

Подсказка 4

Верно! Достаточно отдать всем остальным участникам этого клуба только циркуль, а всем остальным ребятам — только линейку. А что, если клуба из одного человека нет? Можно ли действовать аналогично? И не забудьте проверить, что всё действительно выполняется!

Показать доказательство

Рассмотрим самый маленький по численности участников клуб $A$ (если таких несколько, выберем любой). Одному его участнику (назовем его Паша) выдадим и циркуль, и линейку, остальным участникам этого клуба дадим только циркуль, а всем остальным ребятам — только линейку. Докажем, что условие задачи будет выполняться.

Действительно, рассмотрим произвольный клуб $X.$ Если в нем есть Паша, то условие сразу выполнено. В противном случае клуб $X$ пересекается с клубом $A,$ причём в $X$ есть люди не из $A :$ Паши там нет, а количество людей хотя бы как в $A.$ Таким образом, в $X$ есть люди из $A$ с циркулем и люди из не $A$ с линейкой, что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 3#120662Максимум баллов за задание: 7

Высоты $BE$ и $DK$ параллелограмма $ABCD$ пересекаются в точке $H.$

a) Докажите , что прямые $CH$ и $KE$ перпендикулярны;

б) Найдите длину диагонали $BD$ , если $KE = 3,CH =3,2.$

Замечание. Пункт а) выполнен не во всех случаях.

Источники: Курчатов - 2025, 11.3 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Давайте заметим, что в условии не указано, на какие стороны опущены высоты. Значит, возможно несколько вариантов. Рассмотрите их. На всех ли картинках действительно будет выполняться эта перпендикулярность?

Подсказка 2

Давайте во втором пункте сначала рассмотрим случай, когда высоты BE и DK опущены на AD и AB. Мы хотим связать BD с KE и CH. Это совсем нетрудно сделать, если вспомнить про наличие подобных треугольников, связанных с ортоцентром, и теорему синусов.

Подсказка 3:

Давайте обозначим ∠BAD через γ. Треугольники △AEK и △ABD подобны. А знаете, с каким коэффициентом? Теорему синусов же стоит применять где-то в окружности (CBHD), там тоже фигурирует угол γ.

Подсказка 4:

Во втором случае ситуация иная. Можно сразу вычислить sin(γ), если поработать с окружностью (CKHE). Если дальше вспомнить про подобие, то задача решится)

Показать ответ и решение

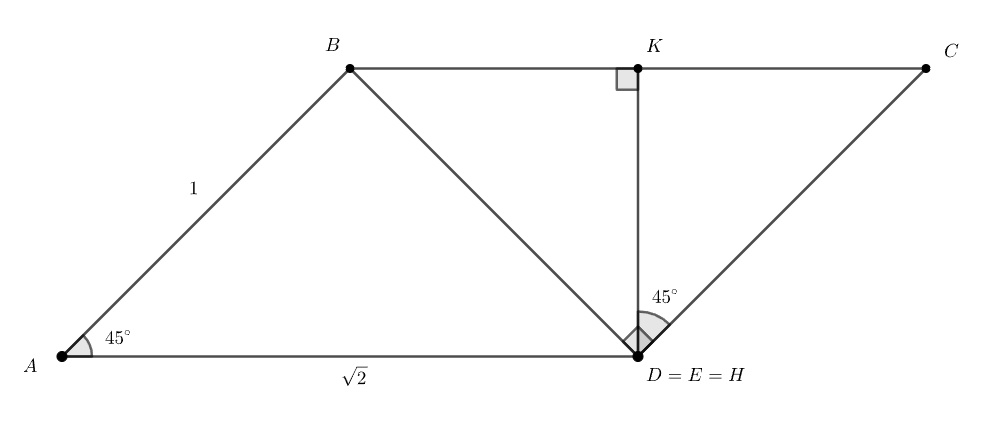
а) Докажем, что в общем случае это неверно. В условии не указаны стороны, на которые опускаются высоты $BE$ и $DK,$ а значит, возможны два варианта: либо точки $E$ и $K$ лежат соответственно на сторонах $AD$ и $AB,$ либо соответственно на сторонах $CD$ и $CB.$ Приведём пример параллелограмма для второго случая, в котором утверждение задачи неверно — пусть $∘ ∠A = 45 ,$ $AB = 1,$ $√ - AD = 2.$ Тогда вершина $D$ совпадает с точками $E$ и $H,$ а точка $K$ является серединой $BC.$ Очевидно, что тогда угол между $CH$ и $KE$ равен $∘ 45 ,$ и они не перпендикулярны.

$PIC$

Замечание. В случае, когда высоты $BE$ и $DK$ опущены на стороны $AD$ и $AB,$ действительно, всегда будет перпендикулярность между прямыми $KE$ и $CH.$

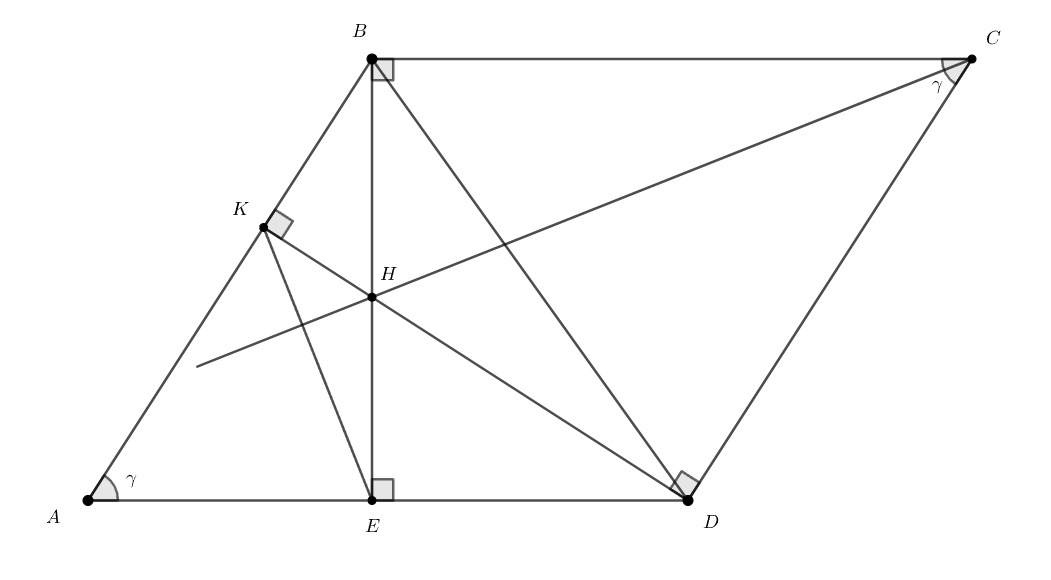
б) Случай $1.$ Рассмотрим случай, когда высоты $BE$ и $DK$ опущены на стороны $AD$ и $AB.$

Пусть $∠BAD = ∠BCD = γ.$ Треугольники $AKE$ и $ABD$ подобны (их углы равны), следовательно,

KE-= AE-= cosγ BD AB

Для треугольника $BCD,$ вписанного в окружность с диаметром $CH,$ верна теорема синусов:

-BD- sinγ = CH

$PIC$

Подставляя известные значения $KE$ и $CH$ получаем:

(|{ BD- sinγ = 3,2 |( cosγ = 3-- BD

Заменяя $BD = x$ и подставляя все в выражение тригонометрического тождества, получаем уравнение:

-x2-+ 32= 1 3,22 x2

4 2 x − 10,24x + 92,16= 0

Полученное квадратное уравнение на $x2$ не имеет решений, так как его дискриминант меньше нуля. Значит, этот случай невозможен.

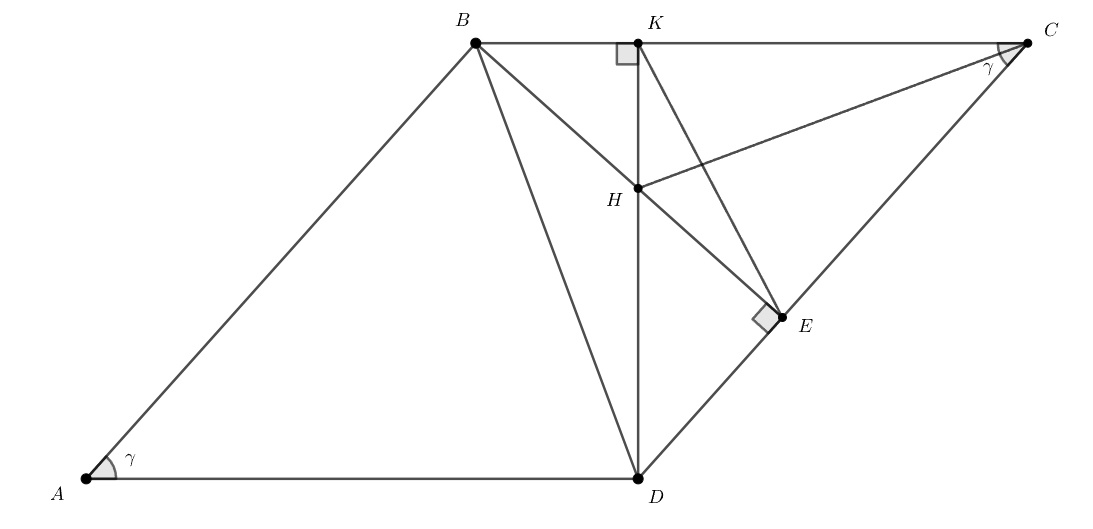
Случай $2.$ Рассмотрим случай, когда высоты $BE$ и $DK$ опущены на стороны $CD$ и $CB.$

Для треугольника $CKE,$ вписанного в окружность с диаметром $CH,$ верна теорема синусов:

-KE- sinγ = CH

Таким образом,

KE- 15 sinγ = CH = 16

Пусть $∠BCD = γ.$ Треугольники $CKE$ и $CDB$ подобны (их углы равны), следовательно,

KE CE ∘------- √31- BD-= BC-= cosγ = 1− sin2γ =-16

Подставляя $KE = 3$ находим:

BD = √48- 31

$PIC$

Ответ:

(a) Неверно в общем случае;

(b) $-48- √31$

Ошибка.
Попробуйте повторить позже

Задача 4#120664Максимум баллов за задание: 7

Пусть $a = [√1]+[√2]+...+[√n]. n$ Докажите, что среди элементов последовательности $a,a ,... 1 2$ есть лишь конечное количество простых чисел, и найдите наибольшее из них.

Источники: Курчатов - 2025, 11.4 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1:

Пусть k — наибольше целое число такое, что k² ≤ n. Значит, n < (k+1)². Ясно, что [√n] = k. Вас это ни на что не наталкивает?

Подсказка 2:

А давайте представим n как k² + t. Но ведь мы же тогда можем вычислить n-й член, используя переменные k и t, потому что t+1 последних слагаемых равны k, следующие k² - (k-1)² слагаемых равны k-1 и так дальше.

Подсказка 3:

Осталось лишь внимательно посмотреть на выражение и заметить, что при k больших некоторого числа оно будет иметь определённый делитель.

Показать ответ и решение

Пусть $k$ — натуральное и $k2 ≤ n< (k +1)2.$ Тогда $[√n]= k.$ Значит, $[√n-]$ принимает фиксированное значение, равное $k,$ пока $n$ пробегает отрезок $2 2 [k ,(k +1) − 1],$ длина которого равна $2k+1.$ Значит, если $2 n = k +t,$ где $0≤ t≤2k,$ то

k∑−1 k∑−1 k∑−1 an = i(2i+ 1)+ k(t+1)= 2 i2+ i+k(t+1)= i=1 i=1 i=1

(k − 1)k(2k− 1) (k − 1)k (k − 1)k(4k+ 1) = -----3------+ --2---+ k(t+ 1)= -----6------+ k(t+ 1)

Заметим, что дробь $(k−1)k(4k+1) ----6----$ принимает целые значения при натуральных $k.$ Если множитель $k$ в числителе этой дроби не сокращается полностью со знаменателем, то данная дробь не взаимно проста с числом $k(t+1)$ (у них обоих есть общий делитель, входящий в $k$ и не сократившийся после деления на $6).$ Ясно, что при $k> 6$ такой множитель заведомо останется. Поэтому $k≤ 6$ и $n ≤72− 1= 48.$ Значит, при $n≥ 49$ все числа $an$ составные.

При $k= 6$ получаем формулу $an =125+ 6(t+ 1),$ где $t≤ 12.$ При $t= 12$ находим $a48 =203= 7⋅29,$ а при $t= 11$ получаем $a47 = 197$ — простое. Таким образом, наибольшее простое число в последовательности $an$ равно $197$ и соответствует индексу $n =47.$

Ответ:

$197$

Ошибка.
Попробуйте повторить позже

Задача 5#120665Максимум баллов за задание: 7

Дана клетчатая доска $6× 6.$ Фигура принц умеет ходить по горизонтали и вертикали, делая ходы сначала на 1 клетку, потом — на две (в одном направлении), потом опять на одну и т.д. Может ли принц, встав на некоторую клетку, обойти все остальные клетки доски, побывав на каждой ровно по одному разу?

Источники: Курчатов - 2025, 11.5 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Попробуем представить некоторые варианты передвижения принца за несколько ходов. Например, как можно обобщить его передвижения за ход вида "2 клетки" от клетки, на которой он был до этого хода?

Подсказка 2

Заметим, что, если мы условно разделим поле на области размера 2х2, то каждый ход вида "2 клетки" принц выходит из одной области и входит в другую. Тогда пусть эти области покрашены в два чередующихся цвета, так, что соседние области имеют разные цвета. Что нам это может дать?

Подсказка 3

Получаем, что на чётных ходах принц будет менять цвет клетки, на которой стоит. Тогда можно условно сопоставить клетки разных цветов по ходам: после второго хода и после первого — разные цвета, после четвертого хода и третьего — разные цвета... и так далее. Тогда как можно оценить количество клеток каждого цвета?

Подсказка 4

То есть свободные варианты для цветов (когда нельзя ходы принца разбить на пары, дающие равное количество обоих цветов) — это только первый и последний ход, что дает максимальное различие в количестве клеток каждого цвета, равное двум. А теперь посмотрим, сколько у нас действительно клеток каждого цвета по нашей раскраске, и сравним результаты.

Показать ответ и решение

Предположим, что такое возможно. Покрасим клетки доски как на рис.

|--|--|-|--|--|--| |1-|1-|2|2-|1-|1-| |1-|1-|2|2-|1-|1-| |2-|2-|1|1-|2-|2-| |2-|2-|1|1-|2-|2-| |1-|1-|2|2-|1-|1-| -1--1--2-2--1--1-|

Заметим, что при втором, четвертом, …, $34$ -м ходе принц меняет цвет клетки. Значит, количество клеток цветов $1$ и $2$ может отличаться не более чем на $2,$ поскольку все клетки, начиная со второй и заканчивая $34$ -й, бьются на пары вторая-третья, четвертая-пятая, …, тридцать четвертая-тридцать пятая, и внутри каждой пары клетки имеют разный цвет. Ну а первая и последняя клетки могут иметь любой цвет.

Таким образом, количество клеток цветов $1$ и $2$ отличается не более чем на $2.$ Но с другой стороны, клеток цвета $1$ больше на $4$ — противоречие.

Ответ:

Нет, не может

Ошибка.
Попробуйте повторить позже

Задача 6#120666Максимум баллов за задание: 7

Найдите все тройки вещественных чисел $x,y,z,$ для которых справедливо равенство множеств:

{ x− y y− z-z-− x} {x,y,z}= y− z ,z− x,x − y

Источники: Курчатов - 2025, 11.6 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Попробуйте рассмотреть, какими могут быть искомые вещественные числа: положительными или отрицательными.

Подсказка 2

Если перемножить xyz в левой части равенства множеств, мы увидим, что оно равно 1, так как равно перемноженной правой части. Тогда попробуйте рассмотреть несколько случаев, связанных с сравнением между собой переменных и 0.

Подсказка 3

Попробуйте составить систему уравнений, руководствуясь сравнением дробей с нулем и друг между друг другом. Попробуйте рассмотреть их числители и знаменатели.

Показать ответ и решение

Заметим, что $xyz = x−-y⋅ y−z⋅ z−x =1, y− z z−x x−y$ поэтому среди чисел $x,$ $y$ и $z$ либо два отрицательных и одно положительное, либо все положительные. Без ограничения общности будем считать, что число $x$ — наибольшее, тогда ясно, что числа $x−y- y−z$ и $y−-z z− x$ имеют разные знаки, значит, $x >0 >y,z.$ Разберем два случая.

Случай 1. $x> 0> y > z$ . В этом случае легко видеть, что $y−z x−-z x−z < x− y$ (числитель меньше числителя, знаменатель больше знаменателя, и все разности положительны). Поэтому $y−z z−-x 0 >z−x > x−y$ и

( |||{ xy − xz =x− y | yz − yx= y− z ||( zx − zy = z− x

Домножая на знаменатели, получаем систему из трех уравнений:

( ||| xy − xz =x− y { yz − yx= y− z |||( zx − zy = z− x

Заметим, что сумма трех этих равенств равна $0,$ поэтому можно рассматривать только первые два. Выражая из второго равенства переменную $y,$ находим $-z--- y = x− z+1.$ Подставляя это выражение в первое равенство и упрощая, получаем:

−1− x − 1 z =--x--, y =1-+x

Когда переменная $x$ будет пробегать все возможные положительные значения, эти две формулы будут описывать соответствующие значения переменных $y$ и $z.$

Заметим, что мы рассматривали случай, когда переменная $x$ — наибольшая. Если придать переменной $x$ отрицательные значения, полученные формулы будут давать ответ в ситуациях, когда наибольшей является переменная $y$ или $z.$ Таким образом, первая серия ответов выглядит следующим образом:

( ) (x,y,z)= t,−--1-,− 1+-t , t∈ℝ ∖{0,−1} t+ 1 t

Случай 2. $x > 0> z > y.$ В этом случае мы получаем аналогичную серию равенств:

x = y− z-, y = x−-y, z = z− x z− x y− z x− y

Домножая на знаменатели, получаем систему из трех уравнений:

( |||{ xz− x2 =y− z | y2− yz = x− y ||( zx − zy = z− x

Складывая эти равенства, получаем формулу $(x− y)(x+ y− 2z)= 0.$ Учитывая, что $x ⁄=y,$ находим $2z = x+ y.$ Тогда $z− x =y − z,$ и первое уравнение нашей системы переписывается в виде $x(z− x)= z− x.$ Вновь вспоминая, что $x⁄= z,$ находим $x =1.$ Остается решить несложную систему:

( {z− yz = z− 1 ( y+ 1= 2z

Решая ее, находим ответ $y = −2$ и $z = − 1 2$ (мы учитываем, что $z >y).$

Вновь циклически переставляя найденные ответы, получаем еще три тройки:

( 1) ( 1 ) ( 1 ) 1,−2,−2 , − 2,1,−2 , −2,−2,1

Ответ:

$(x,y,z)= (t,−-1-,− 1+t), t∈ ℝ∖ {0,−1} t+1 t$

$( 1) ( 1 ) ( 1 ) 1,−2,−2 , − 2,1,−2 , −2,−2,1$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#126190Максимум баллов за задание: 7

Пусть $p(x)=2x3− 3x2+1.$ Рассматриваются два множества $A = {p(2),p(3),...,p(2024)}$ и $B ={p(2)− 1,p(3)− 1,...,p(2024)− 1}.$ В каком из этих множеств квадратов целых чисел больше?

Источники: Курчатов - 2025, 10.1 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Попробуйте разложить многочлен p(x) на множители.

Подсказка 2

Обратите внимание на то, как заданы множества A и B. Попробуйте выразить их элементы.

Подсказка 3

Пусть a = b, тогда если a — квадрат, то и b — квадрат.

Показать ответ и решение

Заметим, что

2 p(x)= (x − 1) ⋅(2x+ 1)

2 p(x)− 1= x ⋅(2x − 3)

Таким образом, при целом $x$ число $p(x)$ является квадратом целого тогда и только тогда, когда квадратом целого является число $2x+ 1,$ а число $p(x)− 1$ — тогда и только тогда, когда квадратом целого является число $2x− 3.$

В первом случае, подойдут нечетные квадраты среди натуральных чисел от 5 до 4049.

Во втором случае, подойдут нечетные квадраты среди натуральных чисел от 1 до 4048.

Так как нечетных квадратов на втором отрезке больше из-за единицы, во втором множестве квадратов целых чисел больше на 1.

Ответ:

Во втором множестве квадратов на 1 больше

Ошибка.
Попробуйте повторить позже

Задача 8#126191Максимум баллов за задание: 7

Имеется таблица $4 ×4,$ в каждой клетке которой стоит 0 или 1. Каждую минуту с ней проделывается следующая операция: для каждой клетки считается сумма чисел в соседних с ней по сторонам клетках и одновременно в каждой клетке число заменяется на 0, если соответствующая сумма четна, и на 1 — если нет. Докажите, что в течение 6 минут какая-нибудь расстановка повторится дважды.

Источники: Курчатов - 2025, 10.2 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

В этой задаче важно обратить внимание на более простые случаи. Рассмотрите таблицы с одной единицей (базисные). Покажите, что их эволюция циклическая. Как симметрия сокращает перебор? Намёк: Достаточно проверить 4 варианта расположения единицы в углу 2×2 из-за симметрии)

Подсказка 2

Любая таблица — сумма базисных. Как операция преобразования действует на такие суммы? Почему это сохраняет свойство цикличности?

Подсказка 3

Для базисных таблиц 3-я и 5-я конфигурации совпадают. Как это гарантирует повторение для произвольной таблицы за ≤6 шагов? Число состояний конечно, то-есть повторение неизбежно, а циклы более простых таблиц ускоряют его.

Показать доказательство

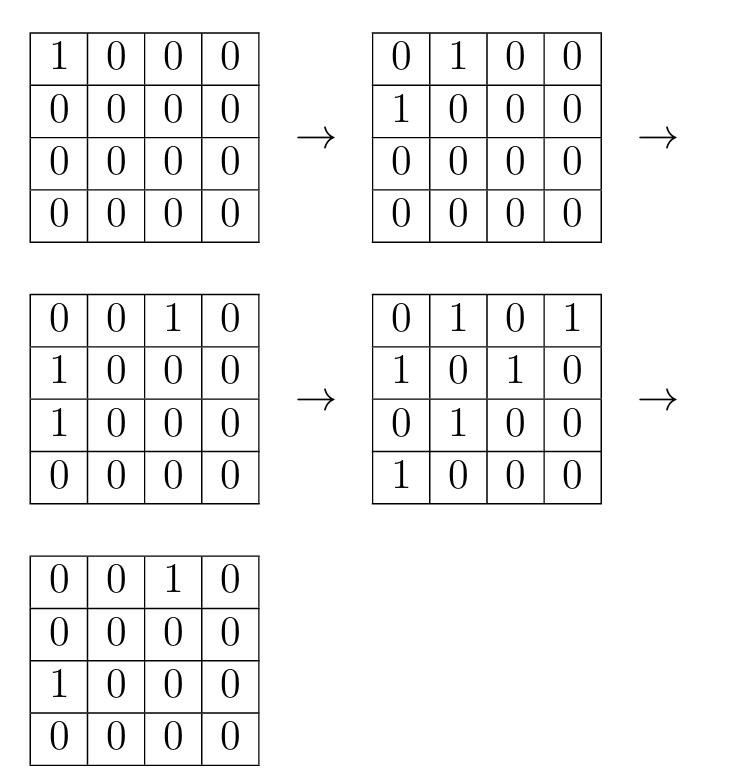
Рассмотрим сначала таблицы, в которых стоит только одна единица (назовем эти таблицы базисными). Докажем перебором, что для таких таблиц условие задачи выполнено.

В силу симметрии конструкции перебор достаточно провести для таблиц, у которых единица стоит в верхнем левом квадрате $2× 2$ (даже в верхнем уголке этого квадрата, так как остальные таблицы получаются из этих подходящим отражением).

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 9#126196Максимум баллов за задание: 7

Дан ромб $ABCD,$ в который вписана окружность. Точки $P$ и $Q$ выбраны на сторонах $AB$ и $AD$ таким образом, что отрезок $PQ$ касается окружности.

(a) Докажите, что площадь треугольника $CPQ$ не зависит от выбора отрезка $PQ.$

(b) Найдите эту площадь, если известна сторона $a$ ромба и его острый угол $α.$

Источники: Курчатов - 2025, 10.3 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Пункт а, подсказка 1

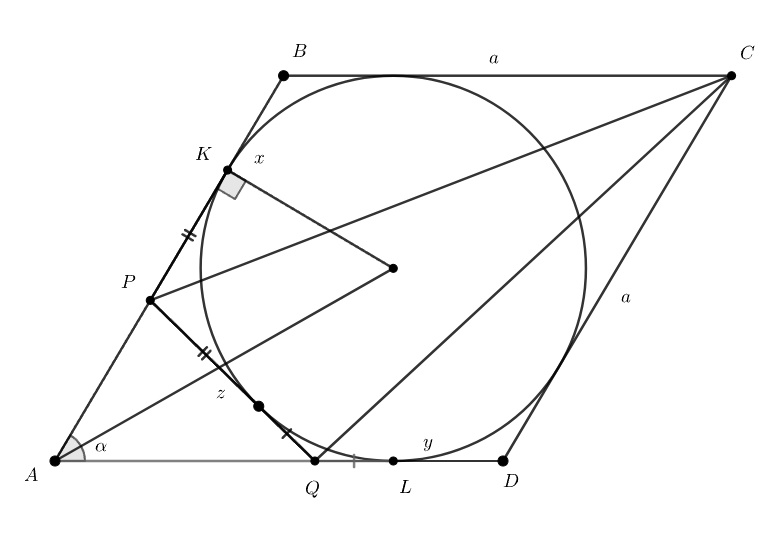
Пусть r — радиус окружности, K и L — точки касания окружности со сторонами AB и AD, сторона ромба равна a, PB = x, QD = y, PQ = z. Попробуйте выразить площадь треугольника CPQ через другие площади.

Пункт а, подсказка 2

S(CPQ) = S(CBPQD) - S(CBP) - S(CDQ).

Пункт a, подсказка 3

S(CPQ) = (a - (x + y - z)/2) ⋅ r. А чему равна сторона BK?

Пункт b, подсказка 1

S(CPQ) = (a - BK) ⋅ r = AK ⋅ r = S(CKA). Чему равен r?

Пункт b, подсказка 2

r = (a/2) ⋅ sin(α).

Показать ответ и решение

$PIC$

(a) Обозначим через $r$ радиус окружности, а через $K$ и $L$ — точки касания окружности со сторонами $AB$ и $AD.$

SCPQ = SCBPQD − SCBP − SCDQ =

= 2a+x-+y-+z-⋅r − (x+ y)r= (a− x+-y− z-)⋅r 2 2

Заметим, что

BK = x-+y-− z, 2

а $BK$ не зависит от выбора точек $P$ и $Q.$

(b) Из пункта a знаем

SCPQ = (a− BK )⋅r= AK ⋅r =SCKA

Кроме того,

r= a sin(α) 2

( α) AK = r⋅ctg 2

Тогда

a2 (α ) SCPQ = -4 sin2(α)ctg 2

Ответ:

(b) $a2-sin2αctg(α∕2) 4$

Ошибка.
Попробуйте повторить позже

Задача 10#126197Максимум баллов за задание: 7

Найдите все натуральные числа, представимые в виде $[a,b]+[b,c]+[c,a]$ для некоторых натуральных $a,b$ и $c$ (здесь $[x,y]$ — наименьшее общее кратное чисел $x$ и $y$ ).

Источники: Курчатов - 2025, 10.4 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Давайте попробует разделить числа по некоторым признакам и доказывать, что одно семейство представимо, а другое — нет.

Подсказка 2

Заметим, что 1 не представляется в таком виде. А как насчёт остальных нечётных чисел?

Подсказка 3

Вспомните, что нечётные натуральные числа — это числа вида 1+2k, где k — натуральное или 0.

Подсказка 4

[1,1] + [k,1] + [1,k] = 1 + 2k, следовательно, все нечётные числа, кроме 1, представимы. Какие еще множества можно выделить?

Подсказка 5

Давайте посмотрим на числа, имеющие нечётный делитель, больший 1.

Подсказка 6

А что значит "нечётный делитель, больший 1"? Какое это число?

Подсказка 7

Должен быть делитель вида 1+2k, где k — натуральное. Попробуйте подобрать такие числа, чтобы в сумме НОК-ов как раз получилось (2k+1).

Подсказка 8

Например, это можно сделать так: [2ˢ, 2ˢ] + [2ˢk, 2ˢ] + [2ˢ, 2ˢk] = 2ˢ(2k+1). То есть, все числа с нечётными делителями рассмотрены. Какие числа осталось рассмотреть?

Подсказка 9

Осталось рассмотреть степени двоек. Попробуйте придумать пример.

Подсказка 10

Вряд ли у Вас получилось. (: Давайте пойдем от противного: предположим, что 2ᵗ представимо. Может, выберем какое-то определенное t для удобства?

Подсказка 11

Выберем наименьшее t. Какими могут быть числа a, b и c?

Подсказка 12

Можно считать, что среди этих чисел есть нечётные, иначе мы бы могли сократить их на 2 и уменьшить минимальное t.

Подсказка 13

Пусть числа a, b — четные, а с — нечетное. Тогда a = 2ᵐa₁, b = 2ⁿb₁, где a₁ и b₁ — нечётные. Давайте попробуем оценить степени вхождения двойки в каждое из слагаемых представления.

Подсказка 14

Рассмотрите возможные отношения между m и n и получите противоречия с величиной t.

Показать ответ и решение

Заметим, что число 1 не может быть представлено в таком виде.

Докажем, что все нечетные числа, кроме единицы, представляются в таком виде:

[1,1]+[k,1]+[1,k]= 2k+ 1,k∈ ℕ

Докажем, что все числа, имеющие нечетный делитель, больший единицы, представляются в таком виде:

s s s s s s s [2 ,2]+ [2 k,2 ]+[2,2 k]= 2 (2k+ 1),k ∈ℕ,s∈ ℕ∪ {0}

Предположим, что степени двойки представляются в таком виде. Тогда число $2t$ представимо. Выберем наименьшее такое $t.$ Без ограничения общности можно считать, что среди чисел $a,$ $b$ и $c$ есть нечетные, ведь иначе мы можем сократить все числа на наименьшую степень вхождения двойки и уменьшить число $t.$

Тогда что среди чисел $a,$ $b$ и $c$ должно быть ровно 1 нечетное и 2 четных. Будем считать, что $c$ — нечетное, $a= 2αa1,$ $b=2βb1,$ где $a1,b1$ — нечетные.

Если $α> β$ (случай $α< β$ аналогичен), то степени вхождения двойки в числа $[a,b],$ $[b,c]$ и $[c,a]$ равны $α,$ $β$ и $α$ соответственно. Но тогда в сумму двойка входит в степени $β,$ поэтому сумма не может равняться степени двойки.

Значит, $α= β.$

α α α α t [2 a1,2 b1]+[2b1,c]+ [c,2a1]= 2

t− a [a1,b1]+[b1,c]+ [c,a1]= 2

Представимая степень двойки уменьшилась, следовательно, мы получили противоречие.

Ответ:

Все натуральные числа, кроме $2t,$ где $t$ — целое неотрицательное число.

Ошибка.
Попробуйте повторить позже

Задача 11#126198Максимум баллов за задание: 7

Найдите количество перестановок ( $a ,a,...,a 1 2 10$ ) набора чисел $(1,2,...,10),$ таких, что $a ≤2a ≤ ...≤ 10a . 1 2 10$

Источники: Курчатов - 2025, 10.5 ( см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Для решения данной задачи необходимо доказать, что количество перестановок чисел a₁; a₂;...; aₙ равно F(n + 1), где F(n) — число Фибоначчи с номером n.

Подсказка 2

Будем доказывать это утверждение по индукции. Для n = 1 и n = 2 можно проверить утверждение перебором (получается, база индукции уже есть!). Для того, чтобы доказать данное утверждение для больших n будем рассматривать такой индекс k, что k-ый член последовательности равен n. Посмотрим тогда внимательно на отрезок [k + 1;n] и подумаем, какие числа могут на нём лежать.

Показать ответ и решение

Докажем следующее утверждение: количество перестановок $a ,a ,...,a 1 2 n$ чисел $1,2,...,n$ таких, что $a ≤ 2a ≤ ...≤ na , 1 2 n$ равно $F , n+1$ где $Fn$ — $n$ -е число Фибоначчи $(F1 =F2 =1,$ $Fk+1 = Fk+ Fk−1).$ Отсюда будет следовать, что ответом является число $F11 = 89.$

Обозначим через $Pn$ количество искомых перестановок длины $n.$ Заметим, что $P1 = 1,$ $P2 = 2.$ Докажем, что $Pn+1 = Pn+ Pn− 1$ при $n ≥ 2.$ Для этого поймем, на какой позиции может стоять в нашей перестановке число $n.$

Пусть $k$ — такой индекс, что $ak = n.$ При $k= n$ мы получаем $an = n,$ количество таких перестановок равно $Pn−1.$ При $k =n − 1$ имеем $nan ≥ n(n − 1),$ тогда $an ≥ n− 1.$ Но $an ⁄= n,$ поэтому $an = n− 1,$ количество перестановок равно $Pn−2.$