Тема Верченко - задания по годам

Верченко 2020

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела верченко - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#123666

Известно, что $p,p,p,p 1 2 3$ — различные простые числа, и $p3− 2p2− 16p =p ⋅p ⋅p − 32. 1 2 3$ Найдите все такие числа $p,p,p ,p . 1 2 3$ Ответ обоснуйте.

Источники: Верченко - 2020, 11.1

Подсказки к задаче

Подсказка 1

Попробуйте преобразовать равенство так, чтобы оно (возможно, не полностью) красиво разложилось на скобки и мы могли сделать выводы о p.

Подсказка 2

Отлично, теперь мы знаем, чему равно (p-2)(p-4)(p+4). Что так и хочется сделать с p₁, p₂ и p₃, чтобы порассуждать об их значениях?

Подсказка 3

Как воспользоваться простотой чисел?

Подсказка 4

Упорядочим p₁, p₂ и p₃ и каждой скобке присвоим значение!

Подсказка 5

Осталось лишь разобрать случаи, каким же простым может быть p. В этом нам может помочь известная идея из теории чисел, которая помогает решать уравнения в целых числах.

Подсказка 6

Рассмотрите равенство по некоторому модулю!

Показать ответ и решение

Так как условие симметрично относительно $p,p ,p, 1 2 3$ тогда, не умаляя общности, считаем, что $p <p < p . 1 2 3$ По условию $3 2 p − 2p − 16p+ 32 =p1⋅p2⋅p3.$ Разложим левую часть на множители:

(p− 2)(p− 4)(p+ 4) =p1⋅p2⋅p3

Непосредственной проверкой убеждаемся, что $p⁄= 2,3,5.$ Значит, $p> 5.$ Следовательно, числа в левой части равенства различны и отличны от $1.$ Поэтому $p− 4= p,p− 2= p ,p+ 4= p . 1 2 3$ Поскольку $p$ на $3$ не делится, возможны случаи:

1.: Число $p$ при делении на $3$ даёт остаток $1.$ Тогда на $3$ делится число $p − 4.$ Такое возможно только, когда $p− 4 =3,$ так как число $p− 4= p1$ — простое. Отсюда $p= 7,p1 =3,p2 = 5,p3 = 11.$
2.: Число p при делении на $3$ дает остаток $2.$ Тогда на $3$ делится $p+ 4.$ Значит $p+4 =3,$ что невозможно.

Ответ:

$p =7,p = 3,p = 5,p = 11, 1 2 3$ при условии $p <p < p 1 2 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#123667

Для зашифрования осмысленного слова его буквы переводят в числа $x ,x ,...,x 1 2 n$ по таблице. Затем выбирают натуральные числа $x 0$ и $k.$ Далее число $x0$ приписывают в начало последовательности $x1,x2,...,xn,$ а число $n+4 xn+1 =x0+ 19$ (где $n−$ длина слова) — в ее конец. Получившаяся в результате последовательность $x0,x1,...,xn,xn+1$ затем преобразуется в последовательность $y0,y1,...,yn,yn+1$ по формуле $( 3 ) yi = r32 xi+ 6xi⋅k + k ,i= 0,1,...,n+ 1,$ где $r32(a)−$ остаток от деления числа $a$ на $32.$ Затем числа $y0,y1,...,yn+1$ заменяют буквами согласно таблице. В результате получили вот что: КЙЫЦНБНЦЛ. Какое слово было зашифровано?


А	Б	В	Г	Д	Е Ё	Ж	3	И	Й	К	Л	М	Н	О	П	Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Ш	Ъ	Ы	Ь	Э	Ю	Я

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31

Источники: Верченко - 2020, 11.2

Подсказки к задаче

Подсказка 1

Да, условие и правда очень мудрёное и не совсем понятно за что ухватиться. Для начала наверное будет хорошо выписать всё, что можем найти. Как насчёт n и последовательности y?

Подсказка 2

Первая и последняя буква в итоговом шифре никак не зависят от изначального слова, но их можно использовать, чтобы найти k. Подумайте, каким образом?

Подсказка 3

Попробуйте рассмотреть остаток от деления от разности последней и первой букв. Может, так получится оценить k?

Подсказка 4

Опробуйте значение k, используйте правило шифрования в обратную сторону и посмотрите, получилось ли осмысленное слово. Если нет, то может стоит попробовать другое значение k?

Показать ответ и решение

В слове КЙЫЦНБНЦЛ $9$ букв, значит $n= 9− 2= 7.$ Найдеём остаток

11 25 5 33 3 r32(19 )= r32((19 )⋅19)= r32(9⋅19)= r32((3 ) ⋅57)= r32((− 5) ⋅(−7))= r32(3⋅25)=11

Преобразуем зашифрованный текст в последовательность чисел:

y0 = 10, y1 =9, y2 = 27, y3 = 22, y4 = 13, y5 = 1, y6 =13, y7 = 22, y8 = 11

Из условия следует, что $x8− x0 = 11.$ Рассмотрим разность

r32(y8− y0)=r32(x8+ 6x8⋅k3 +k − x0− 6x0⋅k3 − k)=

= r32((1 +6k3)⋅(x8− x0))= r32(11⋅(1+ 6k3))

Имеем:

r32(11⋅(1+ 6k3))= 1

Заметим, что $r32(3⋅11)= 1.$ Откуда находим $r32(1+ 6k3)= 3.$ Значит,

1+ 6k3 = 3+32t

3 3k =1+ 16t

3 33k = 11+ 11⋅16t

Значит, $r16(33k3)= r16(k3)= 11.$ В итоге

3 k =11+ 16p

При $p= 1$ получим $k3 =27.$ Отсюда $k =3.$ Опробуем полученное значение.

Согласно правилу зашифрования

y = 9= r (x + 6x ⋅27+ 3)= r (x ⋅3+ 3) 1 32 1 1 32 1

3x1+ 3= 9+32t

3x1 =6+ 32t

Т.е. $r32(3x1)= 6,$ тогда $r32(x1)= 2.$ Продолжая дальше получим:

y2 = 27= r32(x2+ 6x2⋅27+3)= r32(x2⋅3+3)

3x2+3 =27+ 32t

3x2 = 24+ 32t

Т.е. $r32(3x2)= 24,$ тогда $r32(x2)= 8.$ В итоге получим слово ВИСОКОС.

Ответ:

ВИСОКОС

Ошибка.
Попробуйте повторить позже

Задача 3#123668

Каждому из четырех абонентов $A ,A ,A ,A 1 2 3 4$ надо выдать по два уравнения вида $aw +bx+ cy++dz = t,$ где $a,b,c,d,t,w,x,y,z ∈{0,1}.$ Значения секретных битов $w,x,y,z$ одинаковы для всех абонентов и им заранее неизвестны. Приведите хотя бы один пример уравнений, которые надо выдать этим четырем абонентам, чтобы каждая пара ${A1,A3},{A1,A4},{A2,A3}$ могла достоверно вычислить $w,x,y,z,$ но чтобы при этом: $1)$ ни одна другая пара абонентов не могла бы достоверно вычислить более одного секретного бита; $2)$ ни один абонент в одиночку не был в состоянии достоверно вычислить даже один секретный бит. Например, если абонент $A1$ получит уравнения ${w +x +y+ z = 1;w + x+ 0⋅y+0 ⋅z =1},$ а $A2$ — ${w+ 0⋅x+ y+0 ⋅z =0;w+ x+ 0⋅y+ +z = 0}.$ Тогда, объединившись, из имеющихся в их распоряжении четырех уравнений они однозначно найдут, что $w = 1,x =0,y = 1,z =1.$ При этом будем говорить, что пара абонентов ${A1,A2}$ может достоверно вычислить секретные биты $w,x,y,z.$ Здесь традиционно полагается, что $1+ 1= 0.$

Источники: Верченко - 2020, 11.3

Подсказки к задаче

Подсказка 1

Для начала подумайте, как спрятать один конкретных бит z от всех абонентов, кроме конкретной пары.

Подсказка 2

Можно выбрать один конкретный бит и выдать его первому абоненту (уравнением a = p). А второму выдать уравнение a + z = q. Тогда они смогут угадать секретный бит z. Но как спрятать его от остальных? Каким выбрать a?

Подсказка 3

Попробуйте сделать так, чтобы a зависел от других секретных битов.

Показать ответ и решение

"Спрятать"один бит, например, $z,$ от всех абонентов, но сделать его доступным для пары ${A ,A } i j$ можно следующим общим способом: выбрать некоторый бит $a,$ пусть $a= p,$ выдать это уравнение $Ai,$ а уравнение $Aj$ — уравнение $a+ z = q (p,q ∈{0,1}$ — произвольные, но зафиксированные значения). Ни $Ai,$ ни $Aj$ не могут достоверно получить значение бита $z$ из имеющихся у них уравнений, но вместе они смогут его вычислить: $a+a +z =z =p+ q.$

Применительно к задаче, в качестве бита $a$ можно использовать сумму других двух секретных бит. Выдадим абоненту $A2$ уравнение $x +y = p1$ а $A1$ — уравнение $x+ y+ z = q1,$ тогда, сложив эти уравнения вместе, пара абонентов ${A1,A2}$ найдет $z = p1+q1.$ Выдадим абоненту $A2$ также уравнение $x+z =p2,$ тогда они найдут бит $y = p2 +q1.$ Очевидно, что при таком способе, если пара абонентов находит $2$ бита, то она найдет и третий, так как он будет присутствовать хотя бы у одного абонента в линейной комбинации: $x =p1+ p2+q1.$

Этот способ можно распространить и на пары абонентов ${A1,A3},{A1,A4},$ проверяя при этом, что пары абонентов ${A2,A3},{A2,A4},{A3,A4}$ не смогут найти ни одного бита.

Ответ:

Например,

$A1 :w+ x= w0+ x0,x+y =x0+ y0$

$A2 :w+ x= w0+ x0,x+y +z = x0+ y0+z0$

$A3 :y+ z = y0+z0,w+ x+ y = w0+ x0 +y0$

$A4 :w+ x+ y = w0+ x0+ y0,x+ y+ z = x0+y0+ z0$

Ошибка.
Попробуйте повторить позже

Задача 4#123669

Саша решил отправить Маше записку. Для этого каждую букву сообщения он заменил комбинацией из $0$ и $1$ согласно таблице (А— $00000,$ Б— $00001,...,$ Я — $11111).$ Взяв день "Д"и номер месяца "М"своего рождения Саша вычислил $2 2 u1 = Д +M ,u2 = Д ⋅M, u3 = Д− M.$ Далее Саша вычислил четвертое $u4 = r32(u1+ u2u3),$ пятое $u5 = r32(u2+ u3u4),...,$ $n$ -ое число $un =r32(un−3 +un−2un−1),$ где $r32(a)−$ остаток от деления числа $a$ на $32.$ К $i$ -му биту символу исходного сообщения $(0$ или $1)$ он прибавил число $ui$ и взял остаток от деления на $2.$ Полученную последовательность из $0$ и $1$ он вновь преобразовал в буквы по таблице и получил следующее сообщение: ЖДУЛЩБШЛТВШЦЧ. Помогите Маше прочитать его.


A	Б	B	Г	Д	E	Ж	3	И	Й	K	Л	М	H	0	П	P	C	T	У	Ф	X	II	Y	Ш	Ш	T	Ы	Б	9	I0	Я

0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1

0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1

0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Источники: Верченко - 2020, 11.4

Подсказки к задаче

Подсказка 1

Подумайте, как удобнее воспринимать условие «к i-ому биту символу исходного сообщения Петя прибавил u_i и взял остаток от деления на 2»

Подсказка 2

Поскольку результат зависит только от того, четное u_k или нет, то u_i достаточно смотреть на все сравнения по mod 2 вместо mod 32

Подсказка 3

Как четность u_k зависит от четности Д и М?

Подсказка 4

Записка должна нести осмысленное послание. Исключите неподходящие варианты дешифровок.

Показать ответ и решение

По условию, числа $u k$ прибавляются к битам открытого текста, а результат заменяется остатком от деления на 2. Заменим на остатки сразу: $uk = 0,$ если четное, и $uk = 1,$ если нечетное. Это не помешает нам вычислить остаток от деления на 32, так как если число четное, остаток будет четным, иначе — нечетным.

Посмотрим, какие последовательности мы получим в зависимости от четности чисел Д и М:

1.: Числа Д, М — нечетные. Тогда $u1 = 0,u2 = 1,u3 = 0,...$
2.: Числа Д, М имеют разную четность. Тогда $u1 = 1,u2 = 0,u3 = 1,...$
3.: Числа Д, М — четные. Тогда $u1,u2,...,u32 = 0.$ В этом случае текст Машиной записки остался бы без изменения, что, очевидно, не так.

Далее необходимо в первых двух случаях полностью вычислить последовательность ${un},$ вычесть ее из зашифрованного текста (ЗТ) и убедиться, что читаемый вариант получается во втором случае (см. таблицу).

$PIC$

Ответ:

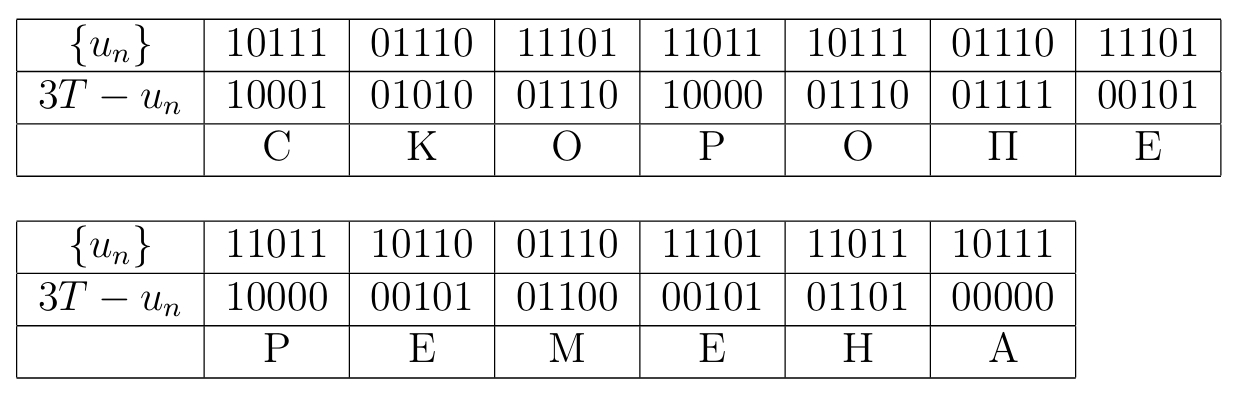
СКОРОПЕРЕМЕНА

Ошибка.
Попробуйте повторить позже

Задача 5#123670

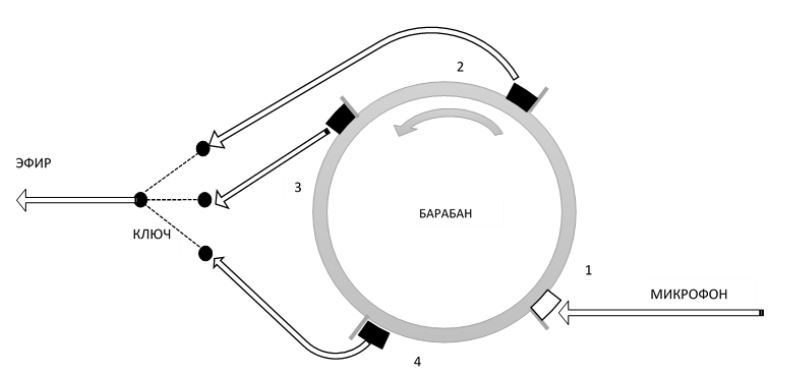
Звук записывается на магнитный слой барабана, который вращается с постоянной скоростью, совершая один оборот за $4$ секунды. Рядом с барабаном по окружности через равные расстояния размещены записывающая $(1)$ и три читающие головки $(2),$ $(3),$ $(4).$ В каждый момент времени в телефонную линию передается сигнал с одной из читающих головок. Устройство спроектировано так, что каждый участок сигнала будет передан в линию один раз, а сама передача стартует, как только начало записи окажется у $3$ -й читающей головки. Сколько различных вариантов звука, переданного в линию, может получиться, если сообщение длилось $20$ секунд?

$PIC$

Источники: Верченко - 2020, 11.5

Подсказки к задаче

Подсказка 1

Пусть передача длилась n секунд. Как можно представить звук, переданный на линию?

Подсказка 2

Переключение между читающими головками происходит раз в секунду, поэтому можно разбить весь звук на n фрагментов и рассматривать их перестановки.

Подсказка 3

Обозначим количество перестановок за T(n). Передача закончится на (n+1)-ой секунде. Какие фрагменты могут быть переданы в этот момент на линию?

Подсказка 4

Мог быть передан n-ый или (n+1)-ый фрагмент. Рассмотрите оба случая.

Подсказка 5

Пусть был передан (n+1)-ый фрагмент. Значит, он не мог быть передан на предыдущей секунде. Чему тогда равно количество перестановок фрагментов?

Подсказка 6

T(n-1). Проведите аналогичные рассуждения для n-ого фрагмента и выведите формулу для T(n).

Показать ответ и решение

Пусть передача длилась $n$ секунд. Так как переключение между читающими головками происходит раз в секунду, весь звук можно разбить на $n$ фрагментов по 1 секунде, тогда звук, переданный на линию, будет будет перестановкой этих фрагментов. Обозначим количество возможных перестановок за $T(n).$

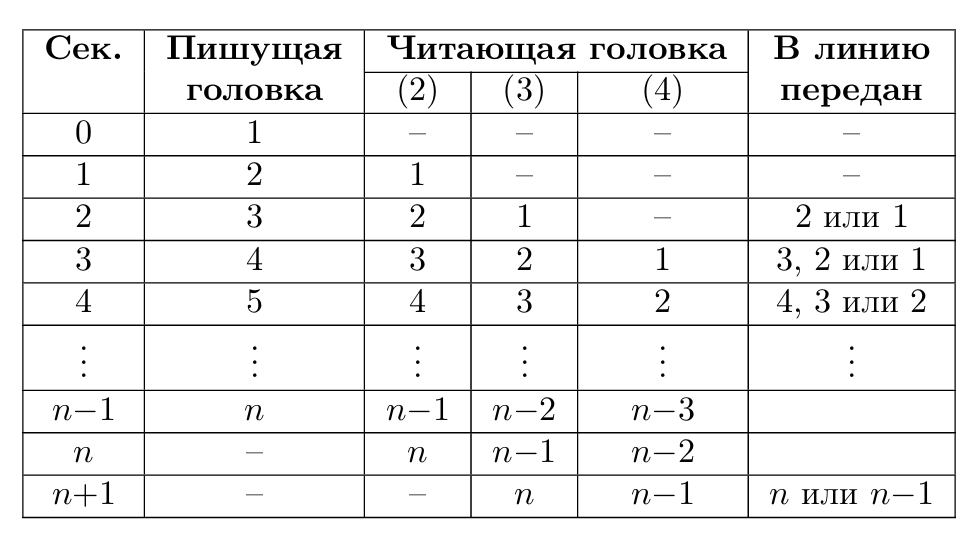
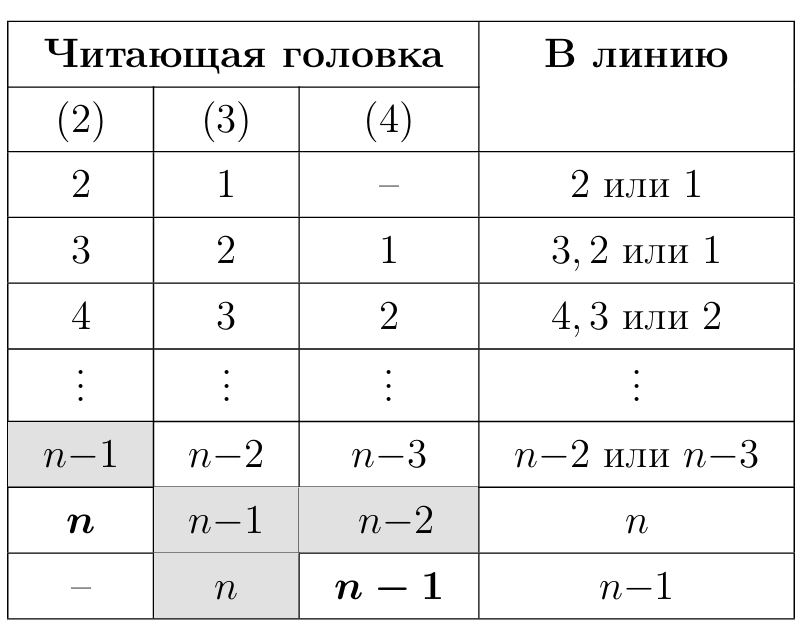
Представим весь процесс в виде таблицы, элементами которой являются номера фрагментов. Например, на второй секунде, с которой начинается передача, на пишущей головке будет третий фрагмент звука, второй фрагмент звука будет на второй читающей головке, а первый фрагмент — на третьей. Передача закончится на $(n +1)−$ ой секунде. В этот момент на линию может быть передан $(n− 1)−$ ый или $n−$ ый фрагмент звука. Рассмотрим оба случая:

$PIC$

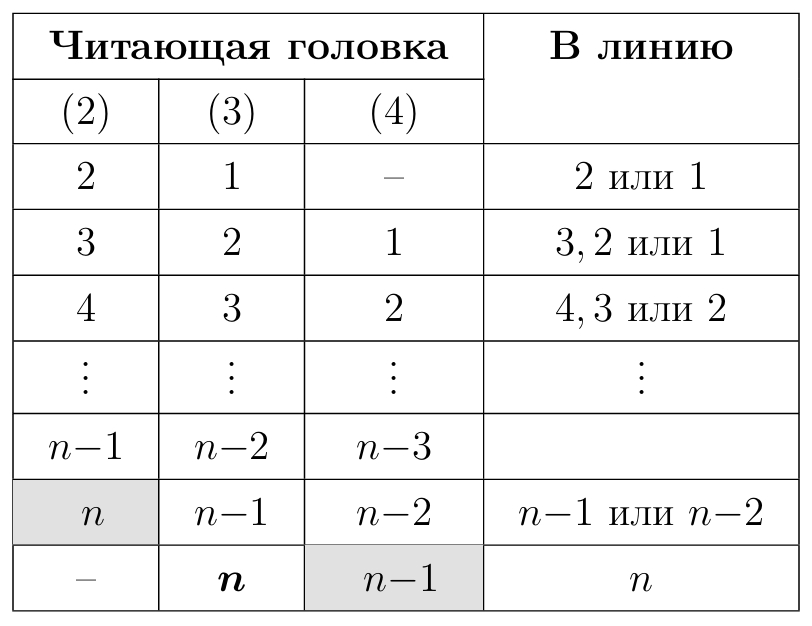
1.: Пусть в момент времени $n +1$ бы передан $n−$ ый фрагмент. Тогда он не мог быть передан на предыдущей секунде. Если посмотреть на таблицу, становится ясно, что количество перестановок фрагментов в этом случае совпадает с $T (n − 1),$ иначе говоря, количеством способов переставить звук длины $n− 1.$

$PIC$
2.: Пусть в момент времени $n+ 1$ бы передан $(n− 1)−$ ый фрагмент. Тогда он не мог быть передан на предыдущих секундах. Так как $n−$ ый фрагмент должен уйти на линию, он должен быть передан в момент $n.$ Тогда до $(n− 1)−$ ой секунды должно быть передано $n − 2$ последовательных фрагмента, что соотвествует $T(n− 2)$ способам.

$PIC$

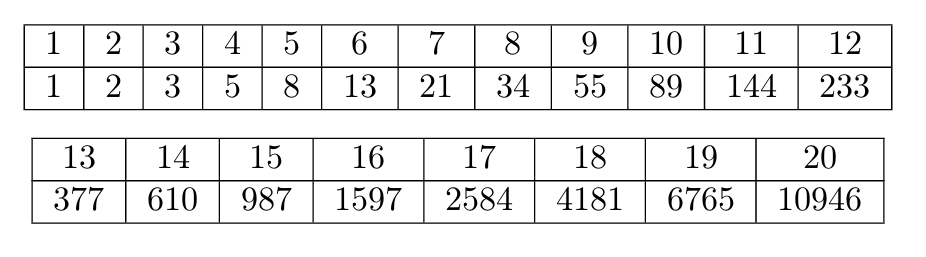
Таким образом, $T(n)=T (n − 1)+ T(n − 2).$ Для любого $n,$ чтобы найти $T(n),$ достаточно найти $T(1)$ и $T(2).$ Останется только с использованием формулы $T(n)= T(n − 1)+ T(n− 2)$ вычислить нужное значение.

$PIC$

Ответ:

$10946$

Ошибка.
Попробуйте повторить позже

Задача 6#123671

Рассмотрим девять чисел $k,...,k , 1 9$ где $k ∈{0,1,2}. i$ При этом хотя бы одно число $k i$ отлично от нуля. С помощью этих чисел вырабатывают последовательность $u1,u2,...,u2019$ по формулам: $u1 = k1,u2 = k2,...,u9 =k9,ui+9 = r3(ui+ ui+1),$ $i= 1,2,...,2010,$ где $r3(a)$ — остаток от деления числа $a$ на $3.$ Найдите такое наименьшее натуральное число $l,$ что какие бы исходные числа $k1,...,k9$ мы ни взяли, в последовательности $u1,u2,...,ul$ каждое из чисел $0,1$ и $2$ гарантированно встретится хотя бы один раз.

Источники: Верченко - 2020, 11.6

Подсказки к задаче

Подсказка 1

Нам никто не говорил, какой конкретный набор для k будет дан. Давайте разбирать все варианты, которые могут возникнуть и мы уже решим задачу! Какой будет самым простым для нас?

Подсказка 2

В наборе k могут быть варианты: встречаются все три числа, набор состоит только из единиц или только из двоек, в наборе есть 1 и 2, но нет 0, в наборе есть только 1 и 0 и последний вариант - в наборе только 0 и 2. Для первых вариантов найти l не составляет проблем, осталось понять, что происходит в последних двух случаях!

Подсказка 3

Отдельного внимания стоит случай, где в k единицы не стоят рядом. Нам опять нужен перебор (посмотрим, что будет, если 1 стоит только на первой и/или последней позициях). Но не забудем, что мы решаем через полный перебор, поэтому остальные случаи тоже требует рассмотрения

Показать ответ и решение

Для каждого набора $k =(k ,...,k ) 1 9$ укажем такое минимальное $l$ , что в соответствующей последовательности $u ,u,...,u 1 2 l$ присутствует каждое из чисел 0, 1 и 2. Затем среди всех таких $l$ останется выбрать наибольшее — это и будет ответом в задаче.

1.

В наборе $k$ встречается каждое из чисел 0, 1 и 2. Тогда искомое $l$ не превосходит 9.

2.

Набор $k$ состоит только из 1. Тогда $u10 =...=u17 = 2$ и $u18 =0.$ Значит, $l= 18.$

Заметим, что случай « $k$ состоит только из 2» эквивалентен, так как если в последовательности ${un},$ отвечающей набору $2k =(2k1,2k2,...),$ заменить все 2 на 1, а 1 — на 2, то получится последовательность, соответствующая набору $k.$

3.

В наборе $k$ присутствуют и 1, и 2, но нет 0. Значит, среди чисел $u1,u2,...,u9$ есть два соседних $(us и us+1),$ одно из которых равно 1, а второе — 2. Тогда $us+9 = 0$ и $l≤ 17.$

4.

Набор $k$ состоит из 0 и 1.

Сразу заметим, что случай « $k$ состоит только из 0 и 2» эквивалентен, так как если в последовательности ${un},$ отвечающей набору $2k = (2k1,2k2,...),$ заменить все 2 на 1, а 1 — на 2, то получится последовательность, соответствующая набору $k.$

Теперь перейдем к разбору. Число 2 впоследствии дадут только две рядом стоящие 1. Поэтому рассматриваем варианты:

а) В $k$ есть рядом стоящие 1. Тогда $l≤19.$

б) В $k$ нет рядом стоящих 1.

Предположим, что 1 есть только на первой и/или последней позициях.

$∙$ Пусть $k = (1,0,...,0).$ В этом случае начало последовательности $u ,u ,... 1 2$ можно вычислить непосредственно:

{un} ={1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,2,1,0,...}

Тогда $l= 27.$

$∙$ Пусть $k = (1,0,...,0,1).$

{un}= {1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,2,1,0...}

Тогда $l= 18.$

$∙$ Пусть $k = (0,...,0,1).$

{un}= {0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,2,1,0,...}

Тогда $l= 26.$

Итак, мы рассмотрели все случаи, когда 1 есть только на первой и/или последней позициях.

Иначе найдется номер $s$ такой, что $2≤ s≤ 8$ и $ks = 1.$ Рядом стоящих 1 нет, поэтому $ks− 1 =ks+1 = 0.$ Тогда $us+8 = us+9 = 1.$ Следовательно, $us+17 = 2$ и $l≤25.$

Ответ:

$l= 27$


A	Б	B	Г	Д	E	Ж	3	И	Й	K	Л	М	H	0	П	P	C	T	У	Ф	X	II	Y	Ш	Ш	T	Ы	Б	9	I0	Я

0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1

0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1

0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1


A	Б	B	Г	Д	E	Ж	3	И	Й	K	Л	М	H	0	П	P	C	T	У	Ф	X	II	Y	Ш	Ш	T	Ы	Б	9	I0	Я

0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1

0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1

0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1


A	Б	B	Г	Д	E	Ж	3	И	Й	K	Л	М	H	0	П	P	C	T	У	Ф	X	II	Y	Ш	Ш	T	Ы	Б	9	I0	Я

0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1

0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1

0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1